Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (2003)

I. David Hilbert was 38 years old when he stepped up to address the Second International Congress of Mathematicians on the morning of Wednesday, August 8, 1900. The son of a judge in the East Prussian capital of Königsberg, Hilbert had made his name as a mathematician 12 years earlier by solving Gordan’s Problem, in the theory of algebraic invariants.

This had been not only a succès d’estime, but also, in a minor way, a succès de scandale. Gordan’s Problem concerned the existence of a certain class of objects. Hilbert had proved that the objects exist but had not produced them, nor even suggested any method for constructing them. Mathematicians refer to this kind of thing as an “existence proof.” Hilbert used the following everyday example in his lectures. “There is at least one student in this class—let us name him ‘X’—for whom the following statement is true: no other student in the class has more hairs on his head than X. Which student is it? That we shall never know; but of his existence we can be absolutely certain.” Existence proofs are rather common in modern mathematics and are nowadays not particularly controversial. Matters were differ-

ent in the Germany of 1888. Just one year previously, Leopold Kronecker, a respected member of the Berlin Academy, had issued his manifesto On the Concept of Number, which attempted to banish from mathematics what he regarded as unnecessary levels of abstraction— anything, in his view, that could not be derived from the integers in a finite number of steps. Gordan himself famously remarked of Hilbert’s existence proof, “This is not mathematics. This is theology.”

The generality of mathematicians, however, acknowledged the validity of Hilbert’s solution. Hilbert then went on to do important work in the theory of algebraic numbers and in the foundations of geometry. He created brilliant new proofs—three and one-half pages for both—of the facts that π and e are transcendental. (When, in 1882, von Lindemann had been the first to prove π transcendental, the aforementioned Kronecker⁵⁸ had complimented him on the elegance of his argument but added that it proved nothing, since transcendental numbers did not exist!) In 1895 Hilbert was given a chair at Göttingen, where he remained until his retirement in 1930.

The names “Hilbert” and “Göttingen” are yoked together in the minds of modern mathematicians as closely as, in other spheres, are “Joyce” and “Dublin,” or “Johnson” and “London.” Hilbert and Göttingen dominated mathematics during the first third of the twentieth century—not merely German mathematics, but all mathematics. The Swiss physicist Paul Scherrer, arriving at Göttingen as a student in 1913, reported finding there “an intellectual life of unsurpassed intensity.” An astonishing proportion of important mathematicians and physicists of the first half of the century had studied either at Göttingen, or under someone who had studied there.

Of Hilbert’s personality, mixed reports have come down to us. By no means antisocial, he was a keen dancer and a popular lecturer. He was also something of a skirt-chaser, to the very limited degree that was possible in the ambience of provincial Wilhelmine Germany. (It is not likely that anything very improper took place.) He had an irreverent streak and seems to have been impatient with the stuffiness of university life, the customs, regulations, and social proscriptions.

One old professor’s wife was scandalized to hear that Hilbert had been seen in the back room of a restaurant in the town, playing billiards with his junior lecturers. When, during World War I, the university refused to give Emmy Noether a regular lecturing position on the grounds that she was a female, Hilbert simply announced a course of lectures to be given by himself, then let Noether deliver them. He seems to have been a soft examiner, always ready to give a candidate the benefit of the doubt.

It is hard to avoid the impression, though, that Hilbert was a man who did not suffer fools gladly, and that he classed rather a large part of humanity as fools. This was particularly unfortunate in Hilbert’s case because Franz, his only child, was afflicted with serious mental problems. Unable to learn anything much, or to hold down any kind of job, Franz also suffered occasional lapses into paranoia, following which he had to be kept in a mental hospital for a while. Hilbert is recorded as saying, at the time of the first of these incarcerations, “From now on I must consider myself as not having a son.”

Hilbert was, at any rate, revered by his students and mathematical colleagues. There is a vast number of anecdotes about him, mostly of an affectionate sort. Here are just three. The first, which touches on the Riemann Hypothesis, I have taken from Constance Reid’s English-language biography.

The second I have borrowed from Martin Davis’s book The Universal Computer.

Hilbert was not, by the way, Jewish, though his given name, unusual among German gentiles, brought him under suspicion in the Hitler years. His paternal ancestors belonged to a fundamentalist Protestant sect called Pietists, who favored Old Testament and hortatory names. Hilbert’s grandfather rejoiced in the names David Fürchtegott Leberecht (i.e., Fear God Live Right) Hilbert.

II. Constance Reid describes Hilbert at the 1900 Congress thus:

Hilbert delivered his address, in German, in a stuffy lecture hall at the Sorbonne. Total attendance at the Congress was 250, but it is not likely that all of them were present to hear Hilbert speak on the morning of August 8.

The title of the address was “Mathematical Problems.” Its opening words became as familiar to twentieth-century mathematicians as those of the Gettysburg Address are to American schoolchildren. “Who of us would not be glad to lift the veil behind which the future lies hidden; to cast a glance at the next advances of our science and at the secrets of its development during future centuries?”⁵⁹ Hilbert went on to speak of the importance of difficult problems in concentrating the attention of mathematicians, inspiring new developments and new symbols, and in pushing mathematics to higher and higher levels of generalization. He ended with a list of 23 particular problems “from the discussion of which an advancement of science may be expected.”

I should like to take you on a tour of Hilbert’s 23 problems.⁶⁰ To do so, however, would make this book unacceptably long. Besides, there is a considerable literature, pitched at many different levels of understanding, providing such tours.⁶¹ I shall only note in passing that the very first of Hilbert’s problems was that of the Continuum Hypothesis, which I mentioned in my previous chapter, and which goes to the heart of the knotty issue of the nature of the real numbers, and of Kronecker’s objections to them. There is a large literature on

the Continuum Hypothesis, too. A good library, or a good internet search engine, will satisfy the curiosity of anyone who wants to look into this fascinating issue.⁶²

Only one of Hilbert’s problems is of direct concern to the topic of this book, and that is the eighth. Here it is, as translated for the Bulletin of the American Mathematical Society by Mary Winston Newson.

8. Problems of Prime Numbers

Some parts of this will be understood by readers who have followed me this far. I hope all of it will make sense by the time I have finished. The main point to note here is that the Riemann Hypothesis was regarded as one of 23 large, difficult issues or problems facing

mathematics in the twentieth century, and it was so regarded by David Hilbert, probably the greatest mathematician doing productive work in 1900.⁶³

III. I briefly mentioned, in Chapter 10.iii, the reason for the prominence of the Riemann Hypothesis at the turn of the century. The main factor was that the Prime Number Theorem had now been proved. Since 1896 it was known, with mathematical certainty, that, yes indeed, π (N) ~ Li(N). Everyone’s attention now focused on that twiddle sign. OK, so as N gets larger and larger without limit, π (N) gets proportionally closer and closer to Li(N). But what is the nature of that closeness? Is a better approximation possible? How approximate is the approximation anyway? What is the “error term”?

Free—now that the proof of the PNT was in the bag—to think about these secondary matters, mathematicians found their eyes being drawn to the Riemann Hypothesis. Bernhard Riemann’s 1859 paper had not, of course, proved the PNT, but it had mightily suggested that it should be true, and even further had suggested an expression for the error term. That expression involved all the non-trivial zeros of the zeta function. Knowing where, precisely, those zeros lie thus became a matter of pressing importance.

The mathematics of all this will become clearer as we go along, but I think you will not be at all surprised to hear that those non-trivial zeros are all complex numbers. In 1900 the following things were known, with mathematical certainty, about the location—the location on the complex plane, that is—of the non-trivial zeros.

• There is an infinity of them, all having real parts between 0 and 1 (exclusive). Using the complex plane to visualize this (see Figure 12-1), mathematicians say that all non-trivial zeros are known to lie in the critical strip. The Riemann Hypothesis makes a much stronger assertion, that they all lie on

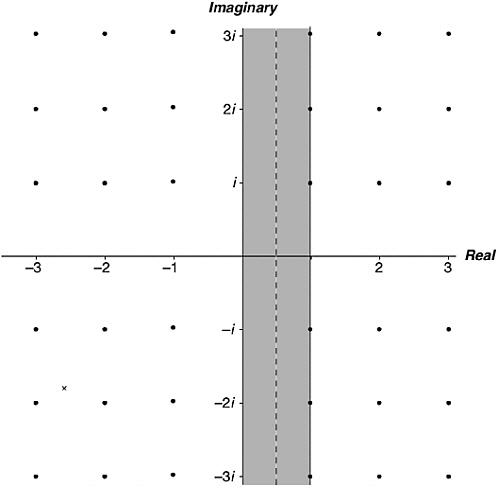
FIGURE 12-1 The critical strip (shaded) and the critical line (dashed).

the line whose real part is one-half, that is, on the critical line. “Critical strip” and “critical line” are common terms of art in discussions of the Riemann Hypothesis, and from now on I shall use them quite freely.

The Riemann Hypothesis (stated geometrically)

All non-trivial zeros of the zeta function lie on the critical line.

• The zeros occur in conjugate pairs. That is, if a + bi is a zero, then so is a – bi. In other words, if z is a zero, then so is its

complex conjugate . I defined “complex conjugate” and the z-bar notation in Chapter 11.v. In yet other words, if there is a zero above the real line, its mirror image below the real line is also a zero (and, of course, vice versa).

• Their real parts are symmetrical about the critical line; that is, a zero either has real part equal to (in line with the Hypothesis), or is one of a pair with real parts and , for some real number α between 0 and , and identical imaginary parts. Real parts 0.43 and 0.57 are an example, or real parts 0.2 and 0.8. Another way of saying this would be: supposing there is any non-trivial zero not on the critical line, its mirror image in the critical line must also be a zero. This follows from that formula in Chapter 9.vi. If one side of that formula is zero, the other side must be too. Leaving aside integer values of s, where other terms in the formula misbehave or go to zero, this formula says that if ζ (s) is zero, then ζ (1 –s) must be zero too. Thus, if is a zero of the zeta function, then so is , and so, by the previous bullet point, is the conjugate .

Little more than this was known when Hilbert gave his address. Riemann had suggested another twiddle formula for the approximate number of zeros with imaginary part between zero and some large number T (see Chapter 16.iv). However, this formula was not actually proved until 1905, by von Mangoldt. The Hypothesis had not been entirely ignored. It turns up as a discussion topic in some mathematical literature of the 1890s, for example in the French problem journal L’Intermediaire de Mathematiciens. To all intents and purposes, though, the mathematicians of the nineteenth century left it to those of the twentieth to take on Bernhard Riemann’s tremendous and subtle conjecture.

IV. The twentieth century was a very … busy century. A great deal happened, in all spheres of human endeavor. This makes it seem, in retrospect, awfully long, far longer than the mere one-and-a-half standard lifetimes that a century actually is. Mathematics, however, moves at a stately pace, and the deep problems tackled by modern mathematicians yield up their secrets only very slowly and reluctantly. The world of any given mathematical specialty is, too, a small one, with its own heroes, folklore, and oral traditions binding the community together in both time and space. From speaking with living mathematicians to gather material for this book, I came to feel that the twentieth century was not such a very long span of time after all, the great names of its early years almost within hailing distance.

I am writing these words, for example, just a week after talking to Hugh Montgomery, a key figure in developments of the 1970s and 1980s (which I shall tell you about in the proper place). Hugh did postgraduate work at Trinity College, Cambridge, in the later 1960s. Among the faculty members he knew personally was John Edensor Littlewood, 1885–1977, who obtained one of the earliest major advances toward the understanding of the Riemann Hypothesis in 1914. “He tried to persuade me to take snuff,” reports Hugh, who still has in his possession handwritten notes from Littlewood. Littlewood could in theory have met and talked mathematics with Riemann’s friend Richard Dedekind, who lived until 1916 and was mathematically active almost to the end of his life … and who had studied under Gauss! (I have not been able to discover if any such meeting took place. It is not actually very likely. Dedekind retired from his professorship at the Brunswick Polytechnic in 1894 and thereafter, according to George Pólya⁶⁴ “lived in a quiet way, seeing very few people.”)

Because of this strong impression of continuity across the period, I am tempted to abandon a strictly chronological approach to the twentieth century. That temptation is strengthened by the nature of developments through that century. The story of the Riemann Hypothesis in the twentieth century is not a single linear narrative, but a number of threads, sometimes crossing, sometimes tangling

with each other. This needs a little preliminary explanation; and the explanation itself needs a preamble, a note about how mathematics developed from 1900 to 2000.

V. Aside from having been distinguished by Hilbert’s Paris address, the year 1900 is, of course, an arbitrary mark. Mathematics has developed steadily and continuously across the modern period. Mathematicians did not go home from their New Years’ parties in the small hours of January 1, 1900 (or 1901, if you like—see Chapter 6.ii) thinking, “It’s the twentieth century! We must move to a higher level of abstraction!” any more than Europeans woke up on the morning of May 30, 1453, thinking, “The Middle Ages are over! We’d better start disseminating printed books, challenging the authority of the Pope, and discovering the New World!” I should hate to have to stand before a jury of my peers and justify the term “twentieth-century mathematics.”

It is nonetheless true that the mathematics of the last few decades has had a distinctive flavor, quite different from the flavor of mathematics as practiced by Gauss, Dirichlet, Riemann, Hermite, and Hadamard. As well as it can be captured in a word, that flavor is algebraic. Here is the beginning of the first proposition in Alain Connes’ Noncommutative Geometry (1990), a pretty typical higher-math text of the later twentieth century.

Algebraic … algebra … And this in a book about geometry! (The 11th word in the statement of the book’s final theorem, by the way, is “Riemannian.”)

What has been happening these past few decades, very roughly, is this. For most of its development, mathematics has been firmly rooted in number. Most of nineteenth-century math was concerned with numbers: whole numbers, rational numbers, real numbers, complex numbers. In the course of this development, new mathematical objects were created, or the scope of existing ones extended—functions, spaces, matrices—and powerful new tools devised for the manipulation of these objects. Still, it was all about numbers. A function maps one set of numbers into another set. The squaring function maps 3, 4, 5 into 9, 16, 25; Riemann’s zeta function maps 0, 1 + i, 2 + 2i into , 0.58216 – 0.92685i, 0.86735 – 0.27513i. Similarly, a space is a set of points, known by their coordinates, which are numbers. A matrix is an array of numbers, and so on. (I shall introduce matrices in Chapter 17.iv.)

In twentieth-century math the objects that had been invented to encapsulate important facts about number themselves became the objects of inquiry, and the techniques that had been developed for investigating numbers and sets of numbers were turned on those objects themselves. Mathematics broke free, as it were, from its mooring in number and soared up to a new level of abstraction.

Classical analysis, for example, concerns itself with the limit of an infinite sequence of numbers or points (with “point” defined by coordinates, which are numbers). A typical product of the twentieth century, by contrast, was “functional analysis,” where the fundamental object of study is sequences of functions, which might or might not converge, and where a function is itself liable to be treated as a “point” in a space of infinitely many dimensions.

Mathematics even turned on itself to such a degree that the very techniques of investigation and proof became objects of inquiry. Some of the most important theorems of twentieth-century mathematics were concerned with the completeness of mathematical systems (Kurt Gödel, 1931) and the decidability of mathematical propositions (Alonzo Church, 1936).

These momentous developments have not yet, even at the opening of the twenty-first century, been reflected in mathematics education, at least up to college-entrance level. Perhaps they cannot be. Mathematics is a cumulative subject. Every new discovery adds to the body of knowledge, and nothing is ever subtracted. When a mathematical truth has been discovered it is there forever, and every succeeding generation of students must learn it. It never (well, hardly ever) becomes untrue or irrelevant—though it might become unfashionable, or be subsumed as a particular case of some more general theory. (And note that in mathematics, “more general” does not necessarily mean “more difficult.” There is a theorem in projective geometry, Desargues’ Theorem, which is easier to prove in three dimensions than in two. Chapter 7 of H.S.M. Coxeter’s Regular Polytopes contains a theorem⁶⁵ that is easier to prove in four dimensions than in three!)

A bright young American turning up for a first class as a college math major learns math pretty much as it was known to the young Gauss, with perhaps a few forward excursions. Since I am pitching my book to readers at about that level, the mathematics you are reading here has a strong nineteenth-century flavor to it. I shall cover all developments down to the present day in these narrative chapters, explaining them as best I can, but my mathematical chapters do not often go beyond 1900.

VI. The story of the Riemann Hypothesis in the twentieth century is the story of an obsession that gripped most of the great mathematicians of the age sooner or later. Instances of this obsession are abundant, as will become clear over the next few chapters. Here I shall just give a single example.

David Hilbert, as I have already described, listed the Riemann Hypothesis eighth in his list of 23 problems for mathematicians of the twentieth century to concentrate their efforts on. That was in

1900, before the obsession took hold. His state of mind a few years later is revealed in the following story, told by his younger colleague George Pólya.

And this was not an era short of challenging problems. Fermat’s Last Theorem (that there are no whole-number solutions to the equation xⁿ + yⁿ = zⁿ when n is greater than 2, proved in 1994) was still open; so was the Four Color Theorem (that four colors are sufficient to color any map in the plane, no two adjacent regions having the same color, proved in 1976); so was Goldbach’s Conjecture (that every even number greater than 2 is the sum of two primes, still unproved); so were many lesser but long-standing problems, conjectures, and conundrums. The Riemann Hypothesis soon came to tower over them all.

The obsession took different mathematicians in different ways, according to their mathematical inclinations. Thus a number of threads developed during the course of the century—different approaches to investigating the Hypothesis, each originated by some one person, then carried forward by others, the threads sometimes crossing and tangling with each other. There was, for example, the computational thread, in which mathematicians set about actually calculating the value of more and more zeros, and developing better methods for doing so. There was an algebraic thread, started by Emil Artin in 1921, attempting to take the Riemann Hypothesis by a flanking movement through an algebraic topic called Field Theory. Later in the century, as a result of a remarkable encounter I shall write about in due course, a physical thread emerged, linking the Hypothesis to

the mathematics of particle physics. While all this was going on, analytic number theorists were still working steadily away, continuing the tradition begun by Riemann himself, tackling the Hypothesis with the tools of complex function theory.

And research into the primes themselves went on, too, without any particular application to the Hypothesis but still, very often, with the hope that new insights into the distribution of the primes might throw light on why the Hypothesis is true—or, as the case may be, false. Key advances here were the development of a probabilistic model for the distribution of primes in the 1930s, and Selberg’s “elementary” proof of the Prime Number Theorem in 1949, which I described in Chapter 8.iii.

In covering these developments I shall try to make it clear at every point which thread I am talking about, though sometimes skipping carelessly from one to another to maintain the overall chronological narrative. Let me begin with a brief introductory remark about the computational thread, since that is the easiest for a non-mathematician to understand. What are the actual values, as numbers, of the non-trivial zeros? How can they be calculated? What are their overall statistical properties, taken as a collectivity?

VII. The first concrete information about the zeros was provided by the Danish mathematician Jørgen Gram, to whom I gave a passing mention in Chapter 10. An amateur mathematician with no university position—his day job was, like the poet Wallace Stevens’s, as an insurance company executive—Gram seems to have been doodling for some years with methods of actually calculating the location of the non-trivial zeros (this was long before the age of computers, of course). In 1903, after settling on a fairly efficient method, he published a list of the “first” 15 zeros—the ones closest to, and above, the real line. Gram’s zeros are shown dotted along the critical line in

Figure 12-2. His list, which contained some slight inaccuracies in the right-most digits, begins

FIGURE 12-2 Gram’s zeros.

Every one of these numbers, as you can see, has real part one-half.⁶⁶ (And the existence of each one, of course, implies a conjugate one below the real axis: , and so on. I shall take this as understood and not mention it again until it becomes important, in Chapter 21.) Therefore, as far as they go, they confirm the truth of the Riemann Hypothesis. But of course they don’t go very far. The number of zeros was known to be infinite—that was implicit in Riemann’s 1859 paper. Do they all have real part one-half? Riemann thought so. That was his mighty Hypothesis. At this point, however, no one had a clue.

When Gram’s list appeared, mathematicians must have looked on it in fascinated awe. The secret of the distribution of prime numbers, which had engaged the attention of mathematicians since the days of the legendary Gauss, was locked up somehow in this string of numbers: But how? Their real parts were certainly one-half, as Riemann had hypothesized; but the imaginary parts showed no apparent order or pattern.

I said “mathematicians must have….” I really should have said “a few continental mathematicians must have….” The obsession with Riemann’s Hypothesis that seized mathematicians during the twentieth century was only just beginning to gather strength in 1905. In some parts of the world, it was hardly known. In the next part of my historical narrative I shall take the reader to England, in the high Edwardian summer of her imperial glory. But first let me show you what the zeta function actually looks like.