Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (2003)

I. In Chapter 9.vi I showed some zeros of the zeta function. I said that every negative even number is a zero of the zeta function: ζ (–2) = 0, ζ (–4) = 0, ζ (–6) = 0, and so on. That gets us a certain way toward understanding the Riemann Hypothesis, which, just to remind you, says that

The Riemann Hypothesis

All non-trivial zeros of the zeta function have real part one-half.

Unfortunately, all those negative even numbers are trivial zeros. So … where are these non-trivial ones? To answer that, I must take you into the realm of complex and imaginary numbers.

A lot of people are alarmed by this topic. They believe imaginary numbers are scary, or fantastic, or impossible—have leaked into mathematics from science fiction somehow. This is all nonsense. Complex numbers (of which imaginary numbers are a special case) came into math from very practical considerations. They were useful

in helping mathematicians solve problems they couldn’t solve otherwise. They are no more imaginary than any other kind of number. When was the last time you stubbed your toe on a seven?

The irrational numbers (like and π ) are actually more mysterious, more intellectually intimidating, and, yes, even scarier, than the square root of minus one. Indeed the irrational numbers have given—and, in the form of the so-called Continuum Hypothesis (see David Hilbert’s address in Chapter 12.ii) continue to give—philosophers of mathematics far more trouble than inoffensive, handy little ever did. There have been determined attempts to reject irrational numbers, even in modern times, and even by important professional mathematicians: Kronecker in the late nineteenth century, Brouwer and Weyl in the early twentieth. For some further remarks on this topic, see Section V in this chapter.

II. To get a balanced view of complex numbers, you really need to understand how a modern mathematician thinks of numbers in general. I’m going to try to give an account of this, including complex numbers in my account. Don’t worry too much about what they are right now; I’ll go into more detail a bit later. I include the complex numbers in these next few paragraphs just for the sake of completeness.

So how does a modern mathematician see numbers? As hollow letters, that’s how. As , , , , and . I have been trying to think of a good, memorably daft, mnemonic for keeping these letters in mind but have so far been unable to come up with anything better than “Nine Zulu Queens Ruled China.”

Perhaps I’m getting ahead of things a bit. Here’s an alternative answer to that question. Mathematicians think of numbers as a set of nested Russian dolls.

• Innermost doll: The natural numbers 1, 2, 3, 4, ….

• Next doll: The integers. That is, the natural numbers together with zero and the negative whole numbers (for example, –12).

• Next doll: The rational numbers. That is, the integers together with all positive and negative fractions (for example, numbers like ).

• Next doll: The real numbers. That is, the rational numbers together with the irrational numbers, like , π , e. (Recall from note 11 to Chapter 3.vi the squareovery by the ancient Greeks that there are numbers that are neither integers nor fractions—irrational numbers.)

• Outermost doll: The complex numbers.

There are several things to notice about this arrangement. The first is that there is a characteristic way to write numbers in each doll.

• Natural numbers tend to be written like this “257.”

• Integers frequently have a sign in front like this “–34.”

• Rational numbers are most often written as fractions. For purposes of writing them in fraction form, rational numbers come in two varieties. Those whose size (that is, ignoring the sign) is less than 1 are called “proper fractions,” while the others are “improper.” A proper fraction is written like this, . An improper fraction can be written in two styles, “vulgar” or “mixed” .

• The most important real numbers have special symbols, like π or e. Many others can be expressed with “closed forms” like or π² / 6. Failing all else, or to give an idea of the actual numerical value of a real number, we write it as a decimal, generally with three trailing dots to mean “this isn’t the whole thing, I could supply more digits if I really had to:” –549.5393169816448223…. Alternatively, we can round it to “five decimal places” (–549.53932) or “five significant digits” (–549.54) or any other level of precision.

• Complex numbers look like this, –13.052 + 2.477i. More on that later.

The next thing to note is that the inhabitants of each Russian doll are honorary inhabitants of the next one out and can, if there is some good reason for it, be written in the style appropriate to the outer one.

• Natural numbers (e.g., 257) are honorary integers, and can be written with a plus sign, like this: +257. When you see an integer with a plus sign in front, you think “natural number.”

• Integers (e.g., –27) are honorary rational numbers, and can be written as fractions whose denominator is 1, like this: . When you see a rational number with denominator 1, you think “integer.”

• Rational numbers (e.g., ) are honorary real numbers, and can be written out as decimals, like this: 0.33333333.… It is an interesting thing about rational numbers that if you write a rational number in decimal form, the decimal digits always repeat themselves sooner or later (unless they just come to a dead stop, like ). The rational number , for example, if written as a decimal, looks like this:

  2.4156088560885608856088….

  All rational numbers repeat like that, no irrational numbers ever do. Which is not to say that an irrational number can’t have some pattern to its digits. The number

  0.12345678910111213141516171819202…

  has a clear pattern, and I could tell you in advance what the hundredth digit is, or the millionth, or the trillionth. (Wanna bet? They are 5, 1, and 1, respectively.) This number is, however, irrational. When you see a real number whose decimal repeats, you think “rational number.”

• Any real number can be written as a complex number. Here is written as a complex number: . More later.

(You can jump over steps in the above list of bullet points and write, for example, a natural number as a real number: 257.0000000000….)

Each family of numbers, each Russian doll, is denoted by a hollow letter. is the family of all natural numbers; is the integers; the rationals; and the reals. Each family is, in a sense, contained in the next one. Each expands the power of math. It lets us do something we couldn’t do with the previous doll. For example, allows us to subtract any two numbers and get an answer, which we couldn’t do with (7 – 12 = ?). Likewise, lets us divide by any number (except zero) and get an answer, which we couldn’t do in (–7 ÷ –12 = ?). And opens the door to analysis, the mathematics of limits, because any infinite sequence of numbers in has a limit in , a thing not true in .

(Recall those sequences and series at the end of Chapter 1. All consisted of rational numbers. Some of them converged to 2, or , or —that is, their limits were also rational. Others, however, converged to , or π, or e—irrational numbers. Thus, an infinite sequence of numbers in may converge to a limit not in . The mathematical term of art is: is not complete. , however, is complete, and so is . This idea of completing will assume new importance when I talk about p-adic numbers in Chapter 20.v.)

There are other categorizations of number within, or cutting across, the

, , , and schema. Prime numbers, to take an obvious case, are a subset of . They are very occasionally referred to collectively as . There is a very important subset of called the algebraic numbers, sometimes also given a hollow letter of its own, . An algebraic number is a number that is a zero of some polynomial with coefficients all in , for example, 2x⁷ – 11x⁶ – 4x⁵ + 19x³ – 35x² + 8x – 3. Among the real numbers, every rational number—and, therefore, every integer and natural number—is algebraic; is a zero of 24565x – 39541 (or a solution of 24565x – 39541 = 0, if you

prefer the language of equations and solutions to the language of functions and zeros). An irrational number might or might not be algebraic. Those that are not are called transcendental. Both e and π are transcendental, as proved by, respectively, Hermite in 1873 and Ferdinand von Lindemann in 1882.

III. You can get another perspective on the matter from the following history of numbers I have made up. “Made up” as in “invented out of whole cloth”—it is entirely false.

John Derbyshire’s Bogus History of Numbers

That account is, I emphasize, totally bogus. Our understanding of numbers did not develop like that at all. Even the order is all wrong. It should be , , , , . Natural numbers were certainly known in prehistoric times. The Egyptians invented fractions early in the third millennium B.C.E. Pythagoras (or one of his disciples) discovered irrational numbers around 600 B.C.E. Negative numbers came in during the Renaissance, by way of accounting (though zero had shown up somewhat earlier). Complex numbers appeared in the seventeenth century. It all grew up haphazardly, chaotically, in the way of most human things. Nor is it true that history has ended. History never ends; as soon as one chess game has been won, another begins immediately.

My little bogus history does show how the Russian dolls fit together, though, and I hope it offers some insight into why mathematicians do not regard imaginary and complex numbers as anything

very peculiar. They are just one more Russian doll, created for practical reasons—to solve problems that could not be solved otherwise.

IV. It is tedious to have to keep writing , so mathematicians substitute the letter i for this quantity. Since i is the square root of minus one, i² =–1. If you multiply both sides of that by i, it follows that i³ =–i. Repeat that process, and you get i⁴ = 1.

What about , , , and so on? Don’t we need symbols for them, too? No. By ordinary rules for multiplying integers, –3 =–1 × 3. Since is just , Power Rule 7 tells me that . (For example, , a fancy way of writing 6 = 2 × 3.) So . Now, is, of course, a perfectly ordinary real number, with a value of 1.732050807568877…. To three places of decimals, therefore, . (In its closed form, this is usually written as .) The same is true of the square root of any other negative number. You don’t need a whole mass of them; you need just i.

Now, i is a very proud number. It is aloof and doesn’t care to mix much with other numbers. If I add 3 to 4 I get 7; the 3-ness of the 3 and the 4-ness of the 4 disappear, absorbed into the 7-ness of the 7. If, by contrast, you add 3 to i, you get … 3 + i. It’s the same with multiplication. When you multiply 5 by 2 the 5-ness and 2-ness are swallowed up by the 10-ness of the result, and vanish without trace. Multiply 5 by i, and you get … 5i. It’s as if the i can’t bear to let go of its identity; or perhaps as if the real numbers know that i just isn’t the same kind of thing as they are.

The result is that once you introduce i into the scheme of things, it spawns a whole new class of numbers like 2 + 5i, –1–i, 47.242– 101.958i, , and every other possible a + bi, where a and b are any real numbers at all. These are the complex numbers. Each complex number has two parts, the real part and the imaginary part. The real part of a + bi is a; the imaginary part is b.

As is the case with the other Russian dolls , , , and , numbers belonging to any inner doll are honorary complex numbers. The natural number 257, for example, is the complex number 257 + 0i; the real number is the complex number . A real number is just a complex number with zero imaginary part.

What about complex numbers with no real part? They are called imaginary numbers. Examples of imaginary numbers are: 2i, –1479i, π i, 0.0000000577i. An imaginary number can, of course, be written as a full complex number, if you want to make a point: 2i can be written as 0 + 2i. If you square an imaginary number, you get a negative real number. Note that this is true even for negative imaginaries. The square of 2i is –4, and the square of –2i is also –4, by the rule of signs.

Adding two complex numbers is a breeze. You just add the real parts, then add the imaginary parts; –2 + 7i plus 5 + 12i would be 3 + 19i. Subtraction likewise; if you subtract instead of adding, the answer is –7 – 5i. For multiplication, you must remember how to multiply out brackets, and keep in mind that i ² =–1. So (–2 + 7i) × (5 + 12i) is –10 – 24i + 35i + 84i², which reduces to –94 + 11i. In general, (a + bi) × (c + di) = (ac – bd) + (bc + ad)i.

Division depends on a simple trick. What is 2 ÷ i? Answer: write it as a fraction, 2 / i. The wonderful thing about fractions is that if you multiply both the top and bottom of a fraction by the same number (not zero), its value does not change: , , and are all ways of writing the same fraction. So multiply top and bottom of 2 / i by –i. Two times –i is, of course, –2i. And i times –i is –i ², which is –(–1), which is 1. Therefore, 2 / i is just –2i / 1, which is –2i.

There is always a way to do this, turning the bottom of a fraction into a real number. Since dividing by real numbers is no mystery, we are home and dry. How do I divide two full-blown complex numbers, say (–7 – 4i) / (–2 + 5i)? I multiply top and bottom of the fraction by –2 – 5i, that’s how. Multiply out the top, (–7 – 4i) × (–2 – 5i) = –6 + 43i. Multiply out the bottom, (–2 + 5i) × (–2 –5i) = 29. Answer:

. You can always turn the bottom of (a + bi) / (c + di) into a real number; just multiply by c – di. The general rule, in fact, is

What is the square root of i? Don’t we have to define a whole other class of numbers to take in ? And so on for ever? Answer: Multiply out the brackets (1 + i) × (1 + i). You will see that the result is 2i. So the square root of 2i is 1 + i. Scaling down, the square root of i must be , which indeed it is.

Complex numbers are wonderful. You can do anything with them. You can even raise them to complex powers, if you know what you are doing. For example, (–7 – 4i)^–2+5i is approximately –7611.976356 + 206.350419i. That, however, is something I shall explain more fully elsewhere.

V. The thing you can’t do with complex numbers is lay them out on a line, as you can with real numbers.

You can visualize the family of real numbers, (which of course includes within itself , , and ) very easily. Just lay it out on a straight line. This way of illustrating the real numbers is called “the real line,” as shown in Figure 11-1.

FIGURE 11-1 The real line.

Every real number is on there somewhere. For example, is a little way east of 1, not quite half way to 2, –π is just slightly west of –3, and 1,000,000 is off in the next county somewhere. I can, of course, show only part of the line on a finite sheet of paper. You must use your imagination.

The real line looks obvious, but in fact it is a very deep and mysterious affair. The rational numbers, for example, are “everywhere dense” on it. That means that between any two rational numbers, you can always find another one. And that means that between any two rational numbers you can find an infinity of other ones. (Look: if, between a and b, I am guaranteed to find c, then between a and c, and between c and b, I am guaranteed to find a d and an e … and so on forever.) That, you can just about visualize. But where do the irrational numbers go? It seems they have to somehow squish in between the rational numbers, which, as I’ve just said, are themselves everywhere dense! While yet managing to be not complete!!

Take that sequence from Chapter 1.vii that closes in on , for example, The terms are alternately less than and greater than , so that is short of by about 0.00000036440355 and exceeds it by about 0.00000006252177. Squeezed in between those two fractions, though, is an infinity of other fractions … and still there is room in there somewhere for . And not only for , either, but for an infinity of other irrationals!

For the amazing thing is that not only is there an infinity of irrationals, and not only are they, too, everywhere dense; but there is a precise mathematical sense in which there are far more irrationals than rationals. This was shown by Georg Cantor in 1874. The number of rational numbers is infinite, and the number of irrational numbers is infinite; but the second infinity is bigger than the first. How on earth do they all fit on the real line? How does such an inconceivably vast number of irrationals squeeze in among the rationals, if the rationals themselves are everywhere dense?

I have no space to go into such things here. My advice is not to think about these matters too much. That way lies madness. (In fact, Cantor ended his life in an asylum, although this was more a consequence of a congenital disposition toward depression aggravated by difficulty in getting his theories accepted than a result of thinking too much about the real line. Those theories are not now

seriously doubted.) Just accept that all real numbers are there on the line somewhere.

But now, where on earth are we going to put the complex numbers? The real line is jammed up—and then some!—with rationals and irrationals. Yet for any real number a, there’s a whole infinity of complex numbers a + bi, with b roaming freely up and down the real line. Where shall we put them all?

That last remark suggests the answer. For each real number, we need a line, and since there is an infinity of reals, we need an infinity of lines, side by side. That means a flat plane. While the real numbers can be spread out for inspection on a line, the complex numbers need a plane—which of course we call “the complex plane.” Every complex number is illustrated by a point somewhere in the plane.

In the complex plane as usually drawn (see Figure 11-2), the real line stretches west-east as usual. Set at right angles to it is a new line going south-north, containing all the imaginary numbers: i, 2i, 3i, and so on. To get to the number a + bi, you go a distance a to the east (west if negative), then b to the north (south if negative). The real line and the imaginary line—they are more commonly called “the real axis” and “the imaginary axis”—cross at zero. Points on the real line have imaginary part zero; points on the imaginary line have real part zero. The point where they cross, the point that is on both, has both real and imaginary parts zero. It is 0 + 0i, that is, zero.

Let me introduce three terms of art. The modulus of a complex number is its straight-line distance from zero. The symbol is |z|, pronounced “mod z.” By Pythagoras’s Theorem, the modulus of a + bi is . It is always a positive number or zero. The amplitude of a complex number is the angle it makes with the positive real line, measured in radians. (One radian is 57.29577951308232… degrees; 180 degrees is π radians.) The amplitude is conventionally taken to be an angle between –π (exclusive) and π (inclusive) radians, and its symbol is Am(z).⁵⁷ Positive real numbers have amplitude zero; negative real numbers have amplitude π ; positive imaginary numbers have amplitude π / 2; negative imaginaries have amplitude –π / 2.

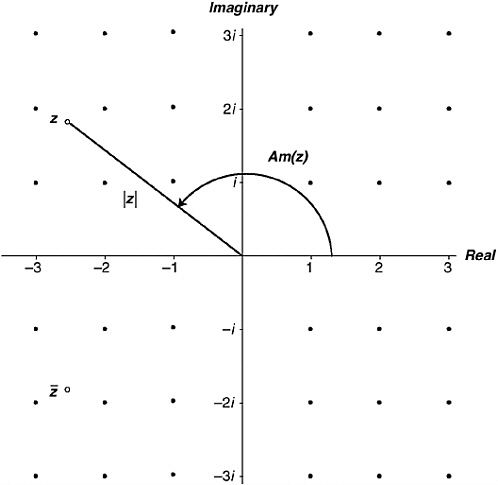
FIGURE 11-2 The complex plane showing a point z (actually –2.5 + 1.8i) with its modulus, amplitude, and conjugate.

Finally, the complex conjugate of a complex number is its mirror image in the real line. The complex conjugate of a + bi is a – bi. Its symbol is , pronounced “z bar.” If you multiply a complex number by its conjugate, you get a real number: (a + bi) × (a – bi) = a² + b², which is, in fact, the modulus of a + bi, squared. That’s what makes the trick for division work. In proper symbols it is , and the division trick is just .

For the complex number –2.5 + 1.8i, shown in Figure 11-2, the modulus is , that is, about 3.080584, the amplitude is about

2.517569 radians (or 144.246113 degrees, if you prefer), and the conjugate is, of course, –2.5 – 1.8i.

VI. To show the complex plane in action, I shall do a wee bit of analysis with complex numbers. Consider the infinite series in Expression 9-2.

(x between –1 and 1, exclusive)

Since there’s nothing involved there but adding, multiplying, and dividing numbers, there seems no reason x should not be a complex number. Does this work for complex numbers? Yes, under certain conditions. Suppose, for example, that x is . Then the series converges. In fact,

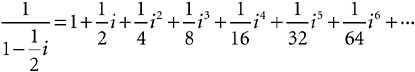
The left-hand side, if you do the trick I described above for division, works out to 0.8 + 0.4i. The right-hand side can be simplified just from the fact that i ² =–1.

You can actually walk out the right-hand side on the complex plane; Figure 11-3 gives the general idea. Start at the point 1 (which is on the real line, of course); then go north to add the ; then go west ; then go south and so on. You get a neat spiral, closing in on the complex number 0.8 + 0.4i. Analysis in action, an infinite series closing in on its limit.

Notice that while we lost the simplicity of one dimension when we moved to complex numbers, we gained some imaginative power.

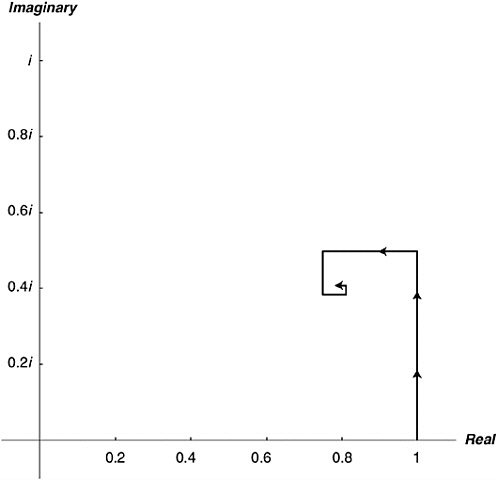
FIGURE 11-3 Analysis in the complex plane.

With two dimensions to play with, you can show mathematical results the way I just did, as striking visual patterns or pictures. This is part of the appeal, for me anyway, of complex analysis. In Chapter 13, I shall actually show you Riemann’s zeta function, and the great hypothesis itself!, laid out as elegant patterns on the complex plane.