Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (2003)

I. I have given over this chapter to two mathematical topics that are related to the Riemann Hypothesis, but not otherwise to each other. The topics are the “big oh” notation and the Möbius mu function. First, big oh.

II. When the great Hungarian number theorist Paul Turán lay dying of cancer in 1976, his wife was at his bedside. She reported that his last murmured words were “Big oh of one….” Mathematicians tell this story with awed admiration. “Doing number theory to the very end! A real mathematician!”

Big oh came into math from Landau’s 1909 book, whose influence, as I have already described, was tremendous. Landau did not actually invent big oh. He candidly acknowledges, on page 883 of the Handbuch, that he borrowed it from Paul Bachmann’s 1894 treatise. It is, therefore, very unfair that it is always referred to as “Landau’s big oh,” and that most mathematicians probably believe Landau did in-

vent it. Big oh is all over the place in analytic number theory, and has leaked into other areas of math too.

Big oh is a way of setting a limit on the size of a function, as the argument goes off (usually) to infinity.

Definition of Big Oh

Function A is big oh of function B if, for large enough arguments, the size of A never exceeds some fixed multiple of B.

Let me take a cue from Paul Turán and consider big oh of one. “One,” as used here, is a function, a function of the simplest kind. Its graph is a flat horizontal line, one unit above the horizontal axis. For any argument at all, the function value is … 1. What, then, does it mean to say that some function f(x) is big oh of one? By the definition I just gave, it means that as the argument x goes off to infinity, f(x) never exceeds some fixed multiple of 1. To put it another way, the graph of f(x) stays forever below some horizontal line. This is useful information about f(x) . There are lots of functions for which this is not true. It’s not true for x², for example, or for x to any positive power, or for e^x, or even for log x.

Big oh means a bit more than that, actually. Note that in my definition I said “the size of A….” That means “the value of A, ignoring its sign.” The size of 100 is 100; the size of –100 is also 100. Big oh doesn’t care about minus signs. To say that some function f(x) is big oh of one is to say that f(x) is forever trapped between two horizontal lines, one above the axis, one an equal distance below it.

As I said, lots of functions are not big oh of one. The simplest is the function x—that is, the function whose value is always equal to the argument. Its graph is a diagonal straight line, disappearing off the graph paper at top right. Clearly it is not contained between any pair of horizontal lines. No matter how far apart you set those horizontal lines, the function x breaks through them eventually. This remains true even if you reduce the slope. The functions 0.1x (shown

in Figure 15-1), 0.01x, 0.001x, 0.0001x all eventually break through any fixed horizontal lines you set as bounds. None is big oh of one.

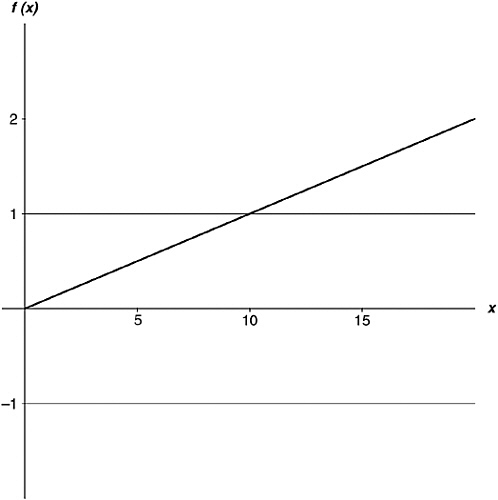
FIGURE 15-1 0.1x is not O(1).

Which illustrates another thing about big oh. Not only does big oh not care about signs, it doesn’t care about multiples, either. If A is big oh of B, then so is ten times A, a hundred times A, a million times A; so is one-tenth of A, one-hundredth of A, one-millionth of A. Big oh doesn’t tell you a precise rate of increase—we have derivatives to do that for us. It tells you the type of rate of increase. The function “one” has no rate of increase at all; it’s dead flat. A function that is big oh of one never increases any faster than that. It might do all sorts of other stuff: dwindle to zero, oscillate indefinitely inside its bounding lines, or approach one of those bounding lines ever more closely, but

it never shoots suddenly upward, or dives suddenly downward, breaking through the lines and staying outside them thereafter.

Those functions 0.1x, 0.01x, 0.001x, 0.0001x are not big oh of one; they are all big oh of x. So is any other function that remains forever trapped in a “pie wedge” between a line ax and its mirror-image line –ax. Figure 15-2 is an example of a function that does not stay thus trapped. This is x², the squaring function. No matter how wide you make the pie wedge—no matter how big the value of a— the graph of x² eventually crashes through the upper line.

FIGURE 15-2 0.1x² is not O(x).

Now you can see the meaning of von Koch’s 1901 result. If the Riemann Hypothesis is true, then the absolute difference between π (x) and Li(x)—either Li(x) – π (x) or π (x) – Li(x), it doesn’t mat-

ter because big oh doesn’t care about signs—stays trapped between two bounding curves as x goes off to infinity. The bounding curves are and its mirror image, for some fixed number C. The error term can do what it likes between those two curves, but it can’t break out from them and suddenly soar away out of their control. The difference between π (x) and Li(x) is big oh of .

Figure 15-3 is an instance of a function that is . The graph shows (1) the curve (top half of the vaguely parabola shape), (2) the mirror-image curve (bottom half of same), and (3) a nonsense function I invented just for illustration, that is . The little “m” stands for “million”—this kind of thing is interesting only for big arguments. Notice that the Derbyshire function actually bursts through its bounds around argument 200m. That’s okay, because it never does it again. The big oh just means that from some point on, forever after, the function stays within its bounds. Trust me, this one does, though obviously I can’t show you the function all the way out to infinity. Big oh doesn’t mind low value exceptions to its rules, which are anyway commonplace in number theory. (Compare: All prime numbers are odd … except the very first.)

Notice also that, since big oh doesn’t care about multiples, the vertical scale is entirely arbitrary. It’s the configuration that matters— the shape of the bounding curves, and the fact that my function from some point on is forever trapped between them.

III. Von Koch’s 1901 result⁸¹—that if the Riemann Hypothesis is true, then —was an early example of a type of result that number theory is now densely populated with, results that begin “If the Riemann Hypothesis is true, then….” If it turns out that the Riemann Hypothesis is not true, quite large parts of number theory will have to be rewritten.

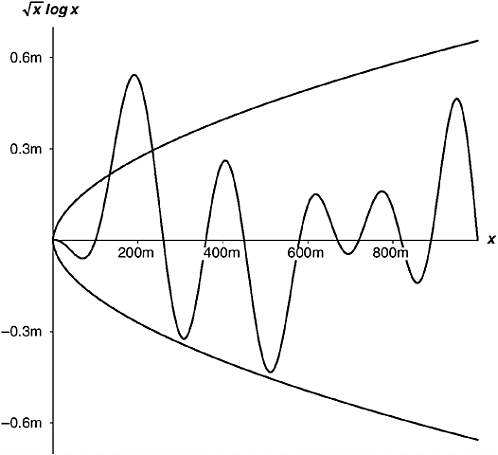
FIGURE 15-3 The Derbyshire function is .

Is there any big-oh type result for the error term Li(x) – π (x) that does not depend on the truth of the Riemann Hypothesis? Oh, yes. It has for decades been a popular sport among analytic number theorists to find ever better big-oh formulas for the error term. None is as good as . That is the bee’s knees, the tightest possible bound on the error term known up to the present. Since it depends on the Hypothesis being true, though, we can’t be certain it applies. The ones we do know for certain are all looser than that. The corresponding parabola shape in Figure 15-3 is a tad wider, the difference getting more and more noticeable as x goes out to infinity. If the Riemann Hypothesis is true, we have the best possible—the tightest—big-oh formula for the error term, so far known. It

is also the simplest. The proven ones we have, the ones that don’t depend on the truth of the Hypothesis, are all rather ugly. Here is the best one I currently know:

where C is a constant number. None of them is much easier on the eye than that.

Compare von Koch’s 1901 result with the italicized words in Hilbert’s eighth problem as I gave them in Chapter 12.ii. Hilbert was echoing Riemann, who says in the 1859 paper that the approximation of π (x) by Li(x) “is correct only to an order of magnitude of .” Now, is of course just . Furthermore, I showed in Chapter 5.iv that log x grows more slowly than any positive power of x, even the teeniest. This can be expressed using big-oh notation thus: For any number ε , no matter how small, log x = O(x^ε ). You can, therefore (well, it’s not immediately obvious, but it’s actually easy to prove), substitute x^ε for log x in ; and since is just , you can add the powers to get . This gives a very popular alternative way to express von Koch’s result, . The symbol ε is so commonly used for vanishingly small numbers that the words “…for any ε , no matter how small” are understood.

Notice, however, that in making this substitution, I weakened von Koch’s result slightly. “” implies “ ”; but the converse is not true. The two results are not precisely equivalent. This is because, as I showed in Chapter 5.iv, not only does log x increase more slowly than any power of x; so does (log x)^N, for any positive N. So if von Koch’s result had stated that the error term was , we could still deduce the alternative form !

Writing von Koch’s result in this slightly weaker form is, though, very suggestive. Riemann was almost right, in the sense that the log function is almost x⁰; the order of magnitude is not , it’s . Given the tools at his disposal, the state of knowledge in the

field, and the known numerical facts at that time, Riemann’s must still count as an intuition of breathtaking depth.⁸²

I introduced big oh with a story, so I shall take my leave of it with another. The point of this story is that mathematicians, like other professionals, sometimes put out a cloud of squid ink to deter and confuse outsiders.

At the Courant conference in Summer 2002 (see Chapter 22), I was talking to Peter Sarnak about this book. Peter is Professor of Mathematics at Princeton University and is an expert on number theory. I mentioned that I was trying to think of a way to explain big oh to readers who weren’t familiar with it. “Oh,” said Peter, “You should speak to my colleague Nick” (i.e., Nicholas Katz, also a professor at Princeton, though mainly an algebraic geometer). “Nick hates big oh. Won’t use it.” I swallowed this and made a note of it, thinking I might find some place for it in this book. Then that evening I happened to be talking to Andrew Wiles, who knows Sarnak and Katz both very well. I mentioned Katz’s not liking big oh. “That’s all nonsense,” said Wiles. “They’re just teasing you. Nick uses it a lot.” Sure enough, he used it in a lecture the next day. Funny sense of humor, mathematicians.

IV. So much for big oh. Now, the Möbius function. There are many ways to introduce the Möbius function. I am going to approach it by way of the Golden Key.

Take the Golden Key and turn it upside down, that is, take the reciprocal of each side in Expression 7-1. Obviously, if A = B and neither is zero, then 1 / A = 1 / B. The result is Expression 15-1.

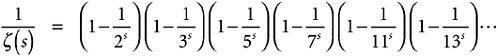
Expression 15-1

I’m now going to multiply out those parentheses on the right-hand side. At first blush this seems like a fairly ambitious thing to want to do. There are, after all, infinitely many of them. It does, in fact, demand a bit more justification and care than I’m going to give it here; but I shall get a useful and true result, so in this case, the end justifies the means.

Multiplying out parentheses is a thing you learn in basic algebra. To multiply out (a + b)(p + q), you first multiply the (p + q) by a to give ap + aq. Then you multiply (p + q) by b to give bp + bq. Then, since the first parenthesis is a plus b, you add the two sub-results together for the final result, ap + aq + bp + bq.

If you have to multiply out three parentheses (a + b) (p + q) (u + v), repeating the process gets you apu + aqu + bpu + bqu + apv + aqv + bpv + bqv. Multiplying out four parentheses (a + b)(p + q)(u + v)(x + y) gives a result like the one in Expression 15-2.

All of this is starting to look a bit formidable. And we have an infinity of parentheses to multiply out! The trick is to look at it with a mathematician’s eyes. What is Expression 15-2 made up of? Well, it’s the sum of a number of terms. What do these terms look like? Take one of them at random, let’s say aqvy. It’s got an a from the first parenthesis, a q from the second, a v from the third and a y from the fourth. It’s a product made up of one number plucked from each parenthesis. And the whole expression is got by adding up the results of all possible combinations of plucks.

Once you have seen this, multiplying out an infinity of parentheses is a breeze. The answer is going to be a sum—an infinite sum, of course—of terms; and each term is got by plucking one number from

each parenthesis and multiplying all those plucked numbers together. If you add up the result of all possible plucks, you have the result. As written, that still looks pretty daunting. It says that every term in my infinite sum is an infinite product. Yes, it is, but since every parenthesis on the right hand of Expression 15-1 contains a 1, I can finesse the situation by plucking an infinity of 1s and only a finite number of not-1s. After all, since every not-1 term in every parenthesis is a number between and 0, if I multiplied an infinity of them, the size of the result (I mean, ignoring the sign) would certainly be no bigger than —which is zero! Watch me build the infinite sum.

First term of the infinite sum: Pluck the 1 from every parenthesis. This gives you the infinite product 1 × 1 × 1 × 1 × 1 × 1 × 1 × …, whose value is of course just 1.

Second term: Pluck the 1 from every parenthesis except the first. From that one, pluck the . This gives the infinite product , which is just .

Third term: Pluck the 1 from every parenthesis except the second. From that one, pluck the . This gives the infinite product , which is just .

Fourth term…. Well, I think you can see that by plucking a 1 from every parenthesis except the nth, I am going to get a term equal to –1 / p^s, where p is the nth prime. So the infinite sum looks like Expression 15-3.

Expression 15-3

That’s not the end of it, though. When you multiply out parentheses, you end up with the sum of all possible terms got by plucking one number out of each parenthesis. Suppose I pluck from the first parenthesis, from the second, and 1 from all the others. This gives me , which is . I shall get a similar term from every possible pair of not-1 plucks. Plucking

from the third parenthesis, from the sixth, and 1 from every other, gives me a term .

(Note that there are two simple rules of arithmetic at work here. One is the rule of signs, a minus times a minus gives a plus. The other is Power Rule 7, (x × y)ⁿ = xⁿ × yⁿ.)

So as well as the terms I’ve already gathered in Expression 15-3, I have a new bunch, of which there is one for every pair of different primes—like 5 and 13—and whose signs are all positive. So now Expression 15-3 has grown to look like this.

with every number in that second row being the product of two different primes.

And we’ve only just started at this business of multiplying out an infinity of parentheses. The next step is to take all possible plucks of three not-1s, with all other plucks equal to 1. An example is , which comes to . Now the result has expanded to

with every number in that third row being the product of three different primes.

Assuming that I can just keep doing this, and assuming that I can rearrange the resulting terms at will, Expression 15-1 boils down to the one shown in Expression 15-4.

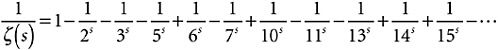
Expression 15-4

The natural numbers that show up on the right-hand side there are … what? Not all the natural numbers, for sure: 4, 8, 9, and 12 are missing. Not the primes: 6, 10, 14, and 15 aren’t primes. If you look back at the process I went through to multiply out that infinity of parentheses, you will see that the answer is: every natural number that is the product of an odd number (including 1) of different primes, prefixed by a minus sign, together with every natural number that is the product of an even number of different primes, prefixed by a plus sign. The numbers that are missing are those like 4, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28, … that divide by some prime squared.

Welcome to the Möbius function, named after the German mathematician and astronomer August Ferdinand Möbius (1790–1868).⁸³ It is universally referred to now by the Greek letter μ , pronounced “mu,” the Greek equivalent of “m.”⁸⁴ Here is a full definition of the Möbius function μ (n).

• Its domain is N, that is, all the natural numbers 1, 2, 3, 4, 5, ….

• μ (1) = 1.

• μ (n) = 0 if n has a square factor.

• μ (n) =–1 if n is a prime, or the product of an odd number of different primes.

• μ (n) = 1 if n is the product of an even number of different primes.

That might seem like an awfully cumbersome function definition to you. However, the Möbius function is tremendously useful in the theory of numbers and will play a starring role later in this book. As an instance of its utility, note that all that laborious algebra I just went through boils down to the elegant result shown in Expression 15-5.

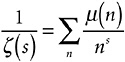
Expression 15-5

V. As important as μ (n) itself in the history of the Riemann Hypothesis is its cumulative value, that is, the number you get if you add up μ (1) + μ (2) + μ (3) + … + μ (k) for some number k. This is “Mertens’s function,” M(k). Its first 10 values (that is, for arguments k = 1, 2, 3, … up to 10) are: 1, 0, –1, –1, –2, –1, –2, –2, –2, –1. M(k) is a very irregular function, oscillating back and forth around zero in the manner of what mathematicians call a “random walk.” For arguments 1,000, 2,000, … up to 10,000 it has the values: 2, 5, –6, –9, 2, 0, –25, –1, 1, –23. For arguments 1 million, 2 million, … up to 10 million it has values: 212, –247, 107, 192, –709, 257, –184, –189, –340, 1,037. If you ignore the signs, it’s pretty clear that the size of M(k) increases, but nothing else is clear.

Because of Expression 15-5, the behaviors of the μ function and the M function (cumulative μ ) are intimately tied up with the zeta function and, therefore, with the Riemann Hypothesis. In fact, if you could prove Theorem 15-1, it would follow that the Riemann Hypothesis is true!

Theorem 15-1

However, if Theorem 15-1 is not the case, it does not follow that the Hypothesis is false. Mathematicians say that Theorem 15-1 is stronger than the Hypothesis.⁸⁵ A slightly weaker version, Theorem 15-2, is precisely as strong as the Hypothesis.

for every number ε , no matter how small.

Theorem 15-2

If Theorem 15-2 is true, the Hypothesis is true; and if it is false, the Hypothesis is false. They are exactly equivalent theorems. More on this in Chapter 20.vi.