Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (2003)

I. The patient reader will have noticed that the mathematical chapters of this book have been moving on two tracks. Chapters 1 and 5 were all about those infinite sums, leading up to a mathematical object named, by Riemann, “the zeta function”; Chapter 3 was concerned with primes, taking its lead from the title of Riemann’s 1859 paper and proceeding from there to the Prime Number Theorem (PNT). Obviously, both issues—the zeta function and the primes—are connected through Riemann’s interest in them. In fact, by yoking the two concepts together in a certain way, by turning the Golden Key, Riemann opened up the whole field of analytic number theory. But how did he do that? What’s the connection? What is the Golden Key? In this chapter I aim to answer that question—to show you the Golden Key. Then I shall begin preparations for turning the Golden Key by offering an improved version of the PNT.

II. It begins with the “sieve of Eratosthenes.” The Golden Key is, in fact, just a way that Leonhard Euler found to express the sieve of Eratosthenes in the language of analysis.³⁴

Eratosthenes of Cyrene (nowadays the little town of Shahhat in Libya) was one of the librarians at the great library of Alexandria. Around 230 B.C.E.—70 years or so after Euclid—he developed his famous sieve method for finding prime numbers. It works like this. First, write down all the whole numbers, starting with 2. Of course, you can’t write them all, so let’s make do with 100 or so.

Now, starting from 2, and leaving 2 untouched, remove every second number from 2 on. The result is

The first number left unscathed after 2 is 3. Leave 3 untouched, but remove every third number from 3 on, if it hasn’t already been removed. The result is

The first number left unscathed after 3 is 5. Leave 5 untouched, but remove every fifth number from 5 on, if it hasn’t already been removed. The result is

The first number left unscathed after 5 is 7. The next step would be to leave 7 untouched, but remove every seventh number from 7 on, if it hasn’t already been removed. The first number left unscathed after 7 would then be 11, and so on.

If you keep doing this for ever, the numbers you are left with are all the primes. That is the sieve of Eratosthenes. If you stop just before processing prime p—that is, just before removing every pth number that wasn’t already removed—you have all the primes less than p². Since I stopped before processing 7, I have all the primes up to 7², which is 49. After that you see some numbers, like 77, that are not prime.

III. The sieve of Eratosthenes is pretty straightforward, and 2,230 years old. How does it get us into the middle of the nineteenth century, and deep results in function theory? Here’s how.

I am going to repeat the process I went through above. (That’s why I went through it so painstakingly.) This time, however, I’m going to apply it to Riemann’s zeta function, which I defined at the end of Chapter 5. Here is the zeta function for some number s bigger than 1.

Note that writing it in this way involves writing out all the positive whole numbers—which is how we started off the sieve of Eratosthenes (except that this time I included 1).

What I’m going to do is multiply both sides of the equals sign by . This gives me

because of Power Rule 7 (which, for example, makes 2^s times 7^s equal to 14^s). Now I’ll subtract the second of these expressions from the first. On the left-hand sides I have one of ζ (s), and I have of it. Subtracting

The subtraction eliminated all the even-numbered terms from the infinite sum. I’m left with just the odd-numbered terms.

Remembering the sieve of Eratosthenes, I’ll now multiply both sides of this equals sign by , 3 being the first unscathed number on the right-hand side.

Now subtract this expression from the one before. When subtracting the left-hand sides, treat as a blob, a single number (which of course it is, for any given s). I have one of this blob, and I have of it. Subtracting, I get of it.

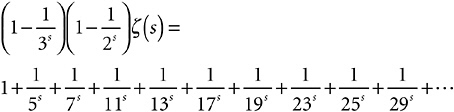
All the multiples of 3 have vanished from the infinite sum. The first unscathed number on the right is now 5.

If I multiply both sides by , the result is

And now, subtracting this equation from the previous one, and this time treating as a single blob, I have one of it, and I have of it. Subtracting

All the multiples of 5 vanished in the subtraction, and the first number left unscathed on the right is 7.

Notice the resemblance to the sieve of Eratosthenes? Actually, you should first notice the difference. When doing the original sieve, I chose to leave each original prime standing, deleting only its multiples by 2, 3, 4, .… Here, I eliminate the original prime from the right-hand side in the subtraction, along with all its multiples.

If I keep doing this up to some decently large prime, let’s say 997, I have this.

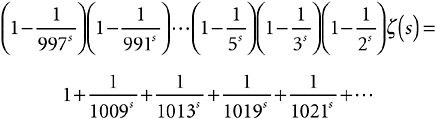
Now, that right-hand side, if s is any number bigger than 1, is just a tiny bit bigger than 1 itself. If s is 3, for example, it works out to 1.00000006731036081534.… So it is not too improbable to say that if you repeated the process forever, you’d get the result shown in Expression 7-1.

Expression 7-1

for any number s bigger than 1, with the left-hand side having one bracketed expression for every prime number, stretching away forever to the left. Dividing each side of the expression repeatedly by each of the parentheses in turn, I get the result shown in Expression 7-2.

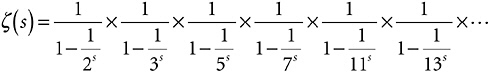
Expression 7-2

IV. That is the Golden Key. To show it to you in all its elegance, let me clean it up a little. I don’t like fractions with fractional denominators any more than you do, and there is a useful bit of mathematical notation I can introduce here to save on typing.

First, remember from Power Rule 5 that a^–N means 1 / a^N, and a^–1 means 1 / a. I can therefore write Expression 7-2 somewhat more succinctly as

There is an even neater way to write this. Recall the Σ notation from Chapter 5.viii. When I am adding up a bunch of terms with the same pattern, I can write the sum in shorthand using the Σ sign. Well, there is an equivalent thing for when I am multiplying terms that all conform to a pattern, the П sign. That’s a capital Greek letter “pi,” for “product.” Here is Expression 7-2 written using the П sign.

This is pronounced “Zeta of s equals the product over all primes of one minus p to the minus s, to the minus one.” The little “p” beneath the П sign is understood to mean “over all primes.”³⁵ Remembering the definition of ζ (s) as an infinite sum, I can rewrite the left-hand side and get Expression 7-3.

The Golden Key

Expression 7-3

Both the sum on the left and the product on the right go all the way to infinity. This, in fact, offers another proof that the primes never end. If they did end, the right-hand side product would end, therefore working out to some finite number, no matter what the value of s. When s = 1, however, the left-hand side is the harmonic series from Chapter 1, which “adds up to infinity.” Since it cannot be the case that an infinity on the left equals a finite number on the right, the number of primes must be infinite.

V. What, you may be wondering, is so all-fired special about Expression 7-3, that I have given it such a grandiloquent name?

The answer to that won’t become entirely clear until a later chapter, when I actually turn the Golden Key. At this point, the main thing to be impressed by—mathematicians, at any rate, find it extremely impressive—is the fact that on the left-hand side of Expression 7-3 we have an infinite sum running through all the positive whole numbers 1, 2, 3, 4, 5, 6, …, while on the right-hand side we have an infinite product running through all the prime numbers 2, 3, 5, 7, 11, 13, ….

Expression 7-3—the Golden Key—is actually named “the Euler product formula.”³⁶ It first saw the light of day, though arranged slightly differently, in a paper with the title Variae observationes circa series infinitas, written by Leonhard Euler and published in 1737 by the St. Petersburg Academy. (The title translates as “Various Observations about Infinite Series”—compare the Latin with the translation, and you can see what I meant back in Chapter 4.viii when I spoke of the ease of reading Euler’s Latin.) The actual statement of the Golden Key in that paper is as follows:

THEOREMA 8

Si ex serie numerorum primorum sequens formetur expressio

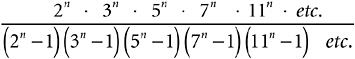
erit eius valor aequalis summae huius seriei

The Latin means “If from the series of prime numbers the following expression be formed … its value will be equal to the sum of this series….” Again, once you know a basic few dozen word endings (“-orum,” a genitive; “-etur,” a present subjunctive passive, etc.), Euler’s Latin holds no terrors.

When jotting down the ideas that make up this book, I first looked through some of the math texts on my shelves to find a proof of the Golden Key suitable for non-specialist readers. I settled on one that seemed to me acceptable and incorporated it. At a later stage of the book’s development, I thought I had better carry out authorial due diligence, so I went to a research library (in this case the excellent new Science, Industry and Business branch of the New York Public Library in midtown Manhattan) and pulled out the original paper from Euler’s collected works. His proof of the Golden Key covers ten lines and is far easier and more elegant than the one I had selected from my textbooks. I thereupon threw out my first choice of proof and replaced it with Euler’s. The proof in part III of this chapter is essentially Euler’s. It’s a professorial cliché, I know, but it’s true nonetheless: you can’t beat going to the original sources.

VI. Having shown you the Golden Key, I now have to begin preparations for turning it. This involves recapitulating a fair amount of math, including a very small quantity of calculus. In the rest of this chapter, I am going to present all the calculus you need to understand the Hypothesis and its significance. Then, making a virtue of necessity, I shall employ that calculus to present an improved version of the PNT—a version much more relevant to Riemann’s work.

Calculus instruction traditionally begins with a graph. The graph I am going to start with is the one in Chapter 5.iii, showing the log function—I have reproduced it here as Figure 7-1. Imagine you are a very small—infinitesimal, if you can manage it—homunculus, climbing up the graph of the log function from left to right. At first, if you start somewhere close to zero, the ascent is very steep, and you need rock-climbing gear. As you go on, however, it gets less and less steep. By the time you get to arguments around 10, you can get upright and actually walk it.

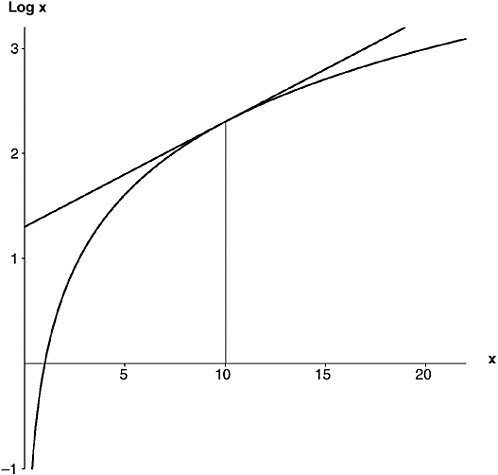
FIGURE 7-1 The function log x.

The steepness of the curve varies from point to point. At every point it has a definite numerical value, though, just as your automobile has a definite speed at any point while you are accelerating— namely, the speed you see if you glance at the speedometer. If you glance again an instant later, you see a slightly different speed; but at every point in time there is some definite speed. Just so, for any argument in its domain (which is all numbers greater than zero), the log function has some definite gradient.

How do we measure that gradient, and what is it? First, let me define “gradient” for a sloping straight line. It is the vertical rise divided by the horizontal span. If, in covering a horizontal distance of 5

units, I rise a vertical distance of 2 units, the gradient is 2 in 5, or 0.4. See Figure 7-2.

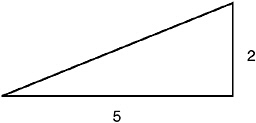
FIGURE 7-2 Gradient.

To get the gradient of a curve at any point, I construct the one straight line that touches the curve at that point. Plainly there is only one such line; if I “roll” the line a little (imagine it’s a steel rod, and the curve a steel band), it touches the curve at a slightly different point. The gradient of the curve at the point is the gradient of that unique touching straight line. The gradient of log x at the argument x = 10 turns out, if you measure it, to be . The gradient at argument 20 is less, of course; it measures . The gradient at argument 5 is steeper; it measures . It is, in fact, yet another amazing property of the log function that the gradient at any argument x is 1 / x, the reciprocal of x, also known as x^–1.

If you ever did a calculus course, this all sounds pretty familiar. The starting point of calculus is, in fact, this: From any function f I can derive another function g, which measures the gradient of f at any argument. If f is log x, then g is 1 / x. This derived function is called, believe it or not, “the derivative” of f. For example, 1 / x is the derivative of log x. If you are presented with some function f, the process of finding the derivative is called “differentiation.”

Differentiation follows some easy rules. It is, for example transparent to several basic arithmetic operations. If the derivative of f is g, then the derivative of 7f is 7g. (So the derivative of 7 times log x is 7 times 1 / x.) The derivative of f-plus-g is the derivative of f plus the derivative of g. This breaks down for multiplication, though; the derivative of f-times-g is not the derivative of f times the derivative of g.

In this book, the only functions besides log x whose derivatives I am concerned with are the simple power functions x^N. I am going to tell you without proving it that for any number N, the derivative of x^N is Nx^N–1. Table 7-1 is a partial table of the derivatives of all the power functions.

Of course x⁰ is just 1, its graph a flat horizontal line. It has no gradient, zero gradient. If you differentiate any fixed number, you get zero. And x¹ is just x; the graph is a straight line going diagonally upward, exiting the graph paper at the top right corner; the gradient is a steady 1. Note that there is no power whose derivative is x^–1, though x⁰ looks to be in the right position. That is not surprising, since we already know that the derivative of log x is x^–1. Once again, log x looks as though it is trying to pass itself off as x⁰.

VII. You no doubt recall my saying more than once that mathematicians love to be able to invert things. Here is P in terms of Q; what is Q in terms of P? That is how I brought up the log function in the first place—as the inverse of the exponential function. If a = e^b, then what is b in terms of a? It’s log a.

Suppose then, that I differentiate function f and get function g. Then g is the derivative of f. And f is the … what? of g? What is the inverse of differentiation? The derivative of log x is 1 / x, so log x is the … what? of 1 / x? Answer: It’s the integral, that’s what. The inverse of a derivative is an integral, and the inverse of differentiation is integration. Since the whole business is transparent to multiplication by a fixed number, turning Table 7-1 upside down and fiddling a little gives the inverse table shown in Table 7-2.

TABLE 7-2 Integrals of x^N.

Function	…	x–3	x–2	x–1	x0	x1	x2	x3	…
Integral	…		–x–1	log x	x				…

And in fact, so long as x is not equal to –1, the integral of x^N is x^N+1/(N + 1). (And looking at that table, you see again how the function log x strives to behave as if it were x⁰, which of course it is not.)

If derivatives are good for telling us the gradient of a function— that is, the rate at which it is changing at any point—what are integrals good for? Answer: For finding the areas under graphs.

The function I’ve shown in Figure 7-3—it is actually the function 1 / x⁴, which is to say of x^–4—embraces a certain area between the arguments x = 2 and x = 3. To calculate that area, you first figure out the integral function of x^–4. That, by the general rule above, is , that is, –1 / (3x³). Like any other function, this has a value for every argument in its domain. To find the area from argument 2 to argument 3, you calculate the value of the integral at argument 3, then calculate the value at argument 2, then subtract the second value from the first.

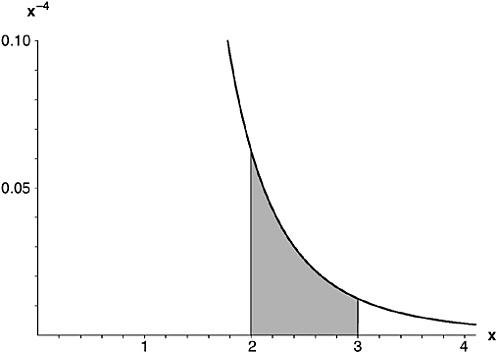
FIGURE 7-3 What integration is good for.

When x = 3, the value of –1 / (3x³) is ; when x = 2 it is . Subtract, remembering that subtracting a negative number is the same as adding the corresponding positive number, , which is , about 0.029321.

Mathematicians have a way to write this, 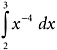, read as “the integral of x to the minus fourth power, with respect to x, from 2 to 3.” (Don’t worry too much about that “with respect to x.” Its purpose is to declare x as the main variable we are working with, whose integral has to be figured out. If there happen to be any other variables under the integral sign, they are just hanging out there; they are not being integrated. Chapter 19 has an illustration.)

Now, sometimes you can let the right-hand end of the integration go off to infinity and get a finite area. It’s like infinite sums. If the values are right, they can converge to a finite value. Same here. If the function is right, the area under it can be finite even though infinitely long. Integrals are connected to sums at a deep level. The integral sign—first used by Leibnitz in 1675—is just an elongated “S” for “sum.”

Look, suppose instead of stopping that area at 3, I took it all the way out to x = 100. Then, since the cube of 100 is 1,000,000, my calculation would have gone like this:

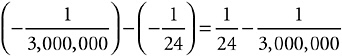
If I went even further, obviously that second fraction would be even smaller. As I head off to infinity, it dwindles away to zero, and I am surely justified in writing . Notice how the x disappears when I actually use integrals to work out an area. I substitute numbers for it, and end up with a number for my answer.

That’s it. That’s all the calculus in this book, I swear. However, although I am not going to introduce any more calculus, I am going to start using calculus right away. I am going to use it to define a

completely new function, one that is terrifically important in the theory of prime numbers and the zeta function.

VIII. First, consider the function 1 / log t. Figure 7-4 shows a graph of it. I have changed my symbol for argument from x to t, because I have a use for x other than as a dummy variable.

I have also shaded an area under the graph, because I am going to do a spot of integration. Integration, as I presented it just now, is a way to calculate the area under a function. First you figure out the integral of the function, then you hit the calculator. So, what is the integral of 1 / log t?

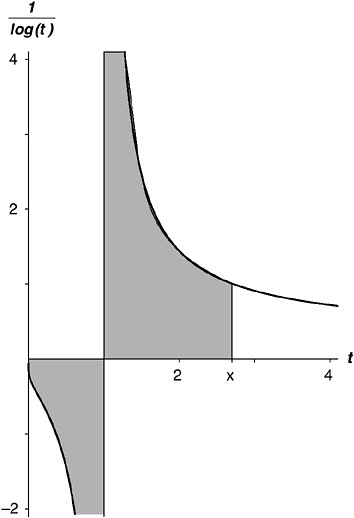
FIGURE 7-4 The function 1 / log t.

Unfortunately, there is no ordinary household function that can be used to express the integral of 1 / log t. This integral is, however, very important. It turns up a lot in our researches into the Riemann Hypothesis. Since we don’t want to keep having to write every time we refer to the darn thing, we simply define it to be a new function, and issue it a certificate declaring it a sound and respectable function in good standing with its peers.

This new function has the name “the log integral function.” The usual symbol for it is Li(x). (Sometimes “li(x).”) It is defined to be³⁷ the area under that graph—the graph of 1 / log t—from zero to x.

This involves a certain sleight of hand, because 1 / log t has no value at t = 1 (because the log of 1 is zero). I am going to skate breezily over that little difficulty, assure you that there is a way to finesse it, and note only that when calculating integrals, areas below the horizontal axis count as negative, so that the area to the right of 1 works to cancel out the area to the left, as t increases. In other words, Li(x) is the shaded area in Figure 7-4, with the negative to the left of t = 1 netted against the positive to the right (when x lies to the right).

Figure 7-5 is a graph of Li(x). Notice that it has negative values when x is less than one (because that area in Figure 7-4 is negative), that it dives off to negative infinity at x = 1 (as you would expect), but that as x advances to the right of 1, the positive area increasingly cancels out the negative so that Li(x) comes back from negative infinity, reaches zero (i.e., the negative area is entirely canceled out) at x = 1.4513692348828…, and thereafter increases steadily. Its gradient at any point is, of course, 1 / log x. And that, please note, is, as I showed in Chapter 3.ix, the probability that a whole number in the neighborhood of x is a prime number.³⁸

Which is why this function is so important in number theory. You see, as N gets larger, Li(N) ~ N / log N. Now, the PNT asserts that

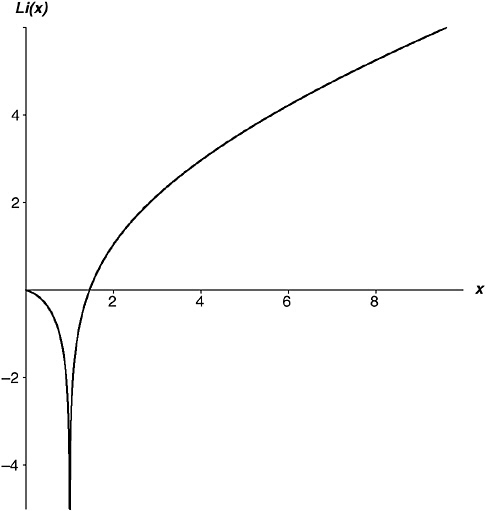
FIGURE 7-5 The function Li(x).

π (N) ~ N / log N. A moment’s thought will convince you that the twiddle sign is transitive—that is, if P ~ Q and Q ~ R, then it must be the case that P ~ R. So if the PNT is true—which we know it is, it was proved in 1896—then it must also be true that π (N)~Li(N).

This is not merely true; it is, in a manner of speaking, truer. I mean, Li(N) is actually a better estimate of π (N) than N / log N is. A much better estimate.

TABLE 7-3

N	π (N)		Li(N) – π (N)
100,000,000	5,761,455	–332,774	754
1,000,000,000	50,847,534	–2,592,592	1,701
10,000,000,000	455,052,511	–20,758,030	3,104
100,000,000,000	4,118,054,813	–169,923,160	11,588
1,000,000,000,000	37,607,912,018	–1,416,706,193	38,263
10,000,000,000,000	346,065,536,839	–11,992,858,452	108,971
100,000,000,000,000	3,204,941,750,802	–102,838,308,636	314,890

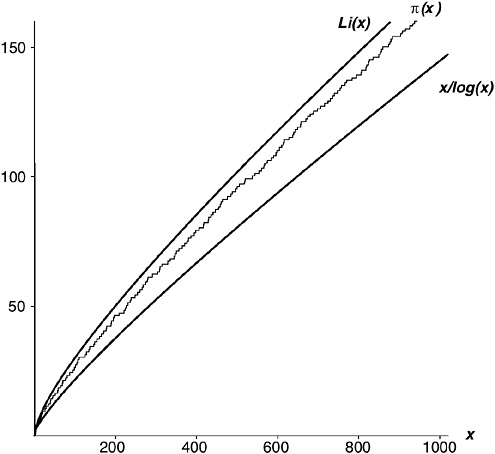
Table 7-3 shows that Li(x) is central to our whole inquiry. In fact, the PNT is most often stated as π (N)~Li(N), rather than as π (N)~N/ log N. Because the twiddle sign is transitive, the two things are equivalent, as can be seen in Figure 7-6. Out of Riemann’s 1859 paper came a precise, though unproven, expression for π (x), and Li(x) leads off that expression.

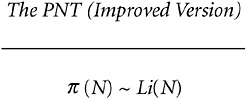
Note just one more thing about Table 7-3. For all the values of N shown in the table, N / log N gives a low estimate for π (N), while Li(x) gives a high one. I am just going to leave that lying there as a comment, for future reference.