Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (2003)

I. —The Basel Problem—

Find a closed form for the infinite series

The Basel problem²⁵ is named from the Swiss city in whose university two of the Bernoulli brothers successively served as professor of mathematics (Jakob, 1687–1705, Johann, 1705–1748). I mentioned in Chapter 1.iii that both Bernoullis found proofs for the divergence of the harmonic series. In the book where he published his brother’s proof, and then his own, Jakob Bernoulli stated the above problem and asked anyone who could figure it out to tell him the answer. (I shall explain the term “closed form” in just a moment.)

Notice that the series the Basel problem is concerned with—I shall call it “the Basel series”—is not far removed from the harmonic series. Each term is, in fact, the square of the corresponding term in the harmonic series. Now, if you square a number smaller than 1, you get a still smaller number; the square of one-half is one-quarter, which is smaller. The smaller the number you start with, the stronger is this

effect; one-quarter is only modestly smaller than one-half, but the square of one-tenth is one-hundredth, which is a lot smaller than one-tenth.

Every term in the Basel series is, therefore, smaller than the corresponding term in the harmonic series, and as you go along they get much smaller. Since the harmonic series only barely diverges, it is not too much to hope that the Basel series, made up of smaller, and then much smaller, terms, converges. Calculation suggests that this is indeed so. The sum of the series to 10 terms is 1.5497677…, the sum to 100 terms is 1.6349839…, the sum to 1,000 terms is 1.6439345…, and the sum to 10,000 terms is 1.6448340.… It really does seem to be converging to some number in the neighborhood of 1.644 or 1.645. But what number?

In situations like this, mathematicians are not satisfied just to get an approximation, especially when the series under investigation converges rather slowly, as this one does. (That sum to 10,000 terms is still 0.006 percent short of the true, final, infinite sum, which is 1.6449340668….) Is the answer a fraction, perhaps, or ? Or something more complicated, perhaps involving roots, , or the fifth root of , or the eighteenth root of 7766? What is it? A lay person might think that it would be satisfying enough to know the number to half a dozen places of decimals. No: mathematicians want to know it exactly, if they can. Not just because they are weird obsessives, but because they know from experience that getting that exact value often opens unexpected doors and throws light on the underlying math. The mathematical term of art for this exact representation of a number is “closed form.” A mere decimal approximation, however good, is an “open form.” The number 1.6449340668… is an open form. Look—those three dots tell you that it is open at the right-hand end, open for you to compute a few more digits, if you feel like it.

That was the Basel problem: to find a closed form for the series of reciprocal squares. The problem was finally cracked in 1735, 46 years

after being posed, by the young Leonhard Euler, toiling away in St. Petersburg. The astonishing answer was π ² / 6. This is the familiar π , the magic number 3.14159265…, the ratio of a circle’s circumference to its diameter. What is it doing in a question that has nothing to do with circles, or with geometry at all? This is not very astounding to modern mathematicians, who are used to seeing π turn up all over the place, but it was very striking in 1735.

The Basel problem opens the door to the zeta function, which is the mathematical object the Riemann Hypothesis is concerned with. Before we can pass through that door, though, I must recapitulate some essential math: powers, roots, and logs.

II. Powers arise in the first place from repeated multiplication. The number 12³ is 12 × 12 × 12, with three multiplicands; 12⁵ is 12 × 12 × 12 × 12 × 12, with five. What happens if I multiply 12³ by 12⁵? That would be (12 × 12 × 12) × (12 × 12 × 12 × 12 × 12), which of course is 12⁸. I just add the powers, 3 + 5 = 8. This is the first great rule of powers.

(Let me just add here that the whole of this section is only concerned with positive values of x. Raising zero to powers is mostly a waste of time, and raising negative numbers to powers brings up tricky problems I shall deal with later.)

What happens if I divide 12⁵ by 12³? That is (12 × 12 × 12 × 12 × 12) / (12 × 12 × 12). I can cancel out three of the twelves top and bottom, leaving 12 × 12, which, of course, is 12². You can see that this is equivalent to just subtracting the powers.

Suppose I cube 12⁵: (12 × 12 × 12 × 12 × 12) × (12 × 12 × 12 × 12 × 12) × (12 × 12 × 12 × 12 × 12) is 12¹⁵. Here the powers are being multiplied.

These are the most fundamental rules for powers. I shall refer to them as “Power Rule 1” and so on throughout this book, without further explanation. I am not quite through with power rules, though. I need to add a few more, because so far I have used only powers that are positive whole numbers. What about negative powers and fractional powers? What about a zero power?

To take the last first, if a⁰ is going to mean anything at all, it might as well be consistent with the power rules I already have, since they are so commonsensical. Suppose I put m equal to n in Power Rule 2; then the right-hand side will indeed be a⁰. The left-hand side will be a^m ÷ a^m. Now, if I divide anything by itself, the answer is 1.

Power Rule 2 can also be used to give meaning to negative powers. Divide 12³ by 12⁵; by Power Rule 2, the answer should be 12^–2. The answer is in fact (12 × 12 × 12) / (12 × 12 × 12 × 12 × 12), which, canceling out three 12s top and bottom, is .

Power Rule 3 gives a clue to what fractional powers ought to mean. What could I do with ? Well, I could cube it; and if I did, by Power Rule 3, I ought to get x¹, which is just x. Therefore, is just the cube root of x. (Definition of “cube root of x”: That number which, if cubed, gives x.) Power Rule 3 then tells us the meaning of

any fractional power; is the cube root of x, squared—or the cube root of x², which works out to the same thing.

Since 12 is 3 × 4, it follows that 12⁵ is (3 × 4) × (3 × 4) × (3 × 4) × (3 × 4) × (3 × 4). This can be rearranged as (3 × 3 × 3 × 3 × 3) × (4 × 4 × 4 × 4 × 4). In a nutshell, 12⁵ = 3⁵ × 4⁵. This is generally true.

What about raising x to an irrational power? What would mean, or 12^π , or 12^e? Here we are back in the realm of analysis. Recall that sequence from Chapter 1.vii, the one that converges to . It looked like this: By taking the sequence far enough, you can get as close as you please to . Now, since Power Rule 6 tells me the meaning of any fractional power, I can work out 12 to the power of any of those fractions. Of course, 12¹ is 12. And is the square root of 12, cubed: 41.569219381…. And is the fifth root of 12, raised to the seventh power, which comes out to 32.423040924…. Similarly, is 33.794038815…, is 33.553590738…, is 33.594688567…, and so on. As you can see, these fractional powers of 12 are closing in on a number—actually, the number 33.588665890…. Since the fractions themselves close in on , I am highly justified in saying that

Given a positive number x, I can, therefore, raise x to any power at all—positive, negative, fractional, or irrational; and doing so always obeys the Power Rules I have stated, because I rigged my definitions to make sure of that! Figure 5-1 shows graphs of x^a for various numbers a, ranging from –2 to 8. Notice particularly the zero-th power of x, which is just a horizontal line at height 1 above the x-axis—what mathematicians call “a constant function” (and Intensive Care Unit nurses call “a flat trace”). For every argument x, the function value is 1. Notice also how fast the whole-number powers of x

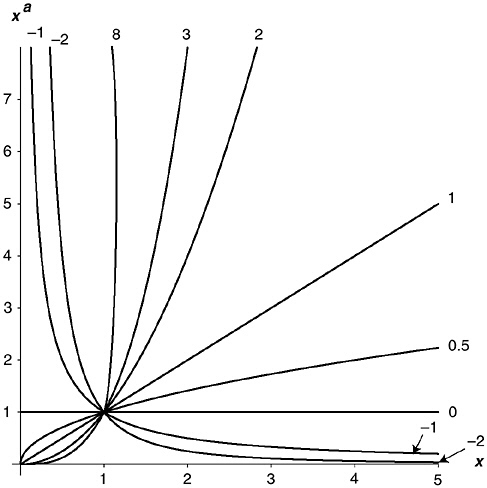
FIGURE 5-1 Powers of x.

(x², x³, x⁸) increase; and, much more to the point of this book, how slowly positive fractional powers like x^0.5 do so.

III. Raising numbers to powers—the proper term is “exponentiation”—is, in the beginning, analogous to multiplication. Multiplication is first presented as repeated addition: 12 × 5 = 12 + 12 + 12 + 12 + 12. Then you move on to a higher level and learn how to do , which is a bit more than just repeated addition. So it is with

powers. We can define 12⁵ very easily. It’s repeated multiplication, 12 × 12 × 12 × 12 × 12. To get to grips with needs more explanation—the explanation I attempted to provide in the previous section.

As I said before, mathematicians love to invert expressions. I have an expression for P in terms of Q? All right, let’s see if I can get Q in terms of P. This is where the analogy between exponentiation and multiplication breaks down. Inverting multiplication is easy. If x = a × b, then a = x ÷ b and b = x ÷ a. Division provides a complete solution to the problem of inverting multiplication.

The analogy breaks down there because, while a × b is always, invariably and infallibly, equal to b × a, it is unfortunately not true, except occasionally and accidentally, that a^b = b^a. (The only whole-number case with different a and b is 2⁴ = 4².) For instance, 10² is 100, but 2¹⁰ is 1,024. If I seek to invert x = a^b, therefore, I am going to need two different methods: one to get a in terms of x and b, another to get b in terms of x and a. The first is a breeze. Raising both sides to the power , Power Rule 3 gives me , which, by Power Rule 6, means that a is the b-th root of x. But what is b in terms of x and a? The Power Rules offer no clue.

This is where logs make their appearance. The answer is, b is the log of x to base a. That is just the definition of log. The log of x to base a (generally written “log_a x”) is defined to be the number b that makes x = a^b true. From this flows the whole family of log functions: log of x to base 2, log of x to base 10 (which older readers will remember as an aid to calculation taught in high schools up to about 1980), and so on. I could present them all in graphs, as I did the graphs of x^a in Figure 5-1.

I am not going to do this because I am deeply indifferent to all members of the log family except one, log to base e, where e is the extremely important, though unfortunately irrational, number 2.71828182845…. Log to the base e is the only kind of log I care about, and the only kind I shall use in this book. In fact, I shall not say “log to base e” any more, just “log.” So what is the log of x? By the above definition, it is the number b that makes x = e^b a true statement.

Since log x is the b that makes x = e^b a true statement, it is obvious that x = e^{log x}. This is just the definition of “log x” written mathematically; but it is so important in what follows that I am going to make a rule out of it.

That is true for every positive number x. The log of 7, for example, is 1.945910…, because 7 = 2.718281^1.945910, to six decimal places. Negative numbers don’t have logs (though this is another thing I reserve the right to change my mind about later); zero doesn’t have a log, either. There is no power you can raise e to with a negative or zero result. The domain of the log function is all positive numbers.

The log function is everywhere in this region of math. We have already seen it in Chapter 3.viii-ix, in the Prime Number Theorem and its equivalents. It will show up again and again in this book in everything to do with prime numbers and the zeta function.

With the log function all over like this, I should give some more detailed coverage of it. Figure 5-2 is a graph²⁶ of log x, for arguments out to 55. I’ve particularly marked the function values for arguments 2, 6, 18, and 54. These arguments go up in multiples of 3; and you can see from the graph that the corresponding function values go up in equal steps—that is, by addition. That’s the point I made about the log function in Chapter 3.viii.

It’s worth enlarging on a little. The great thing about the log function is that it turns multiplication into addition. Look at those lines I marked on the graph. The arguments are 2, 6, 18, 54—I start with 2, multiply by 3, multiply by 3 again, then multiply by 3 again. The function values, holding myself to four places of decimals here, and putting up with a small rounding error, are 0.6931, 1.7918, 2.8904, 3.9890—which start with 0.6931, add 1.0987, add 1.0986, then add 1.0986 again. The log function turned multiplication (by 3) into addition (of log 3, which is 1.09861228866810…).

FIGURE 5-2 The log function.

This follows from the definition of log x and from the Power Rules. From Power Rule 8, if a and b are any two positive numbers, a × b = e^{log a} × e^{log b}. But from Power Rule 1, I can replace the right-hand side like this, a × b = e^{log a + log b}. However, a × b is just a number itself, and so, from Power Rule 8 again, a × b = e^{log (a×b)}. Equating the two different expressions I just got for a × b gives a new Power Rule.

This is a wonderful thing. It means that, when faced with a difficult problem involving multiplication, by “taking logs” (i.e., by ap

plying the principle that if P = Q, it must also be the case that log P = log Q) we can reduce it to a problem in addition, which may be more manageable. It sounds almost trivial; yet this little tool is exactly what I shall need, in Chapter 19.v, to turn the Golden Key.

Since log(a × b) = log a + log b, it follows that log(a × a × a × …) = log a + log a + log a.… This gives the last of my Power Rules.

Without chasing down the logic, let me just tell you that it applies to all powers of a, including fractional and negative ones. A very important particular case is log (1 / a) = – log a, because 1 / a is just a^–1. So once you know that log 3 is 1.09861228866810…, you immediately know that That’s why the graph of log x dives down to negative infinity as x gets closer and closer to zero. This fact, too, will help me turn the Golden Key.

IV. Log x increases slowly, as you can see. The slowness with which log x increases is a very fascinating and important thing all by itself. The main point is that log x increases slower than any power of x. At first thought, that might seem to be very obvious. When I say “power of x,” you probably think of squares and cubes; and you know that a graph of the squaring function or the cubing function zooms up out of sight as the argument increases, way beyond the feeble inching-up of the log function. True, but that’s not the point. What I have in mind here is not a power like this, x², or like this, x³, but rather a power like this, x^0.1.

Figure 5-3 shows some graphs of x^a for small numbers a. I’ve chosen a = 0.5, 0.4, 0.3, 0.2, and 0.1 (with the log function—dotted line—for comparison). You can see that the smaller a is, the flatter the graph of x^a is. You can also see that for values of a below a certain

FIGURE 5-3: The functions x^a, for small positive a.

point (actually, for a less than 1 / e, which is 0.3678794…) the log curve cuts the curve x^a not very far east (never further than e^e, which is 15.1542…).

Well, no matter how small you make a, the graph of log x is eventually flatter than the graph of x^a. If a is bigger than 1 / e, this is true already, even in this diagram. If a is less than 1 / e, then by going far enough east—by taking a big enough argument x—the log x curve eventually cuts the x^a curve again, and then, forever after, lies below it.

Of course, you might have to go some way out. The log curve recrosses the x^0.3 curve slightly east of x = 379; it re-crosses the x^0.2 curve around x = 332,105; it does not re-cross the x^0.1 curve until past x = 3,430,631,121,407,801. If I were to plot the graph of x to the power

of one trillionth, (that is, of x^{0.000000000001}), it would look pretty darn flat. It would, in fact, be hard to distinguish from the “flat trace” at a height of 1 above the x-axis—not at all like that elegant ascending curve of the log function. The log curve would cross it a tiny distance east of e. It’s increasing, though, even if terrifically slowly, and the log curve is getting flatter; and sooner or later they re-cross, and then, forever after, the log curve lies below the x^{0.000000000001} curve. The crossing point in this particular case actually occurs at an argument too big for me to write out; the number starts: 44,556,503,846,304,183 … and continues for a further 13,492,301,733,606 digits.

It’s as if log x were trying to be x⁰. It is not x⁰, of course; for any positive number x, x⁰ is defined to be 1, by Power Rule 4. Its graph is the flat trace, as I showed earlier. Yet even though log x is not equal to x⁰, it nonetheless manages to dip below, and stay below, x^ε , for any number ε , no matter how tiny, when x is large enough.²⁷

The matter is, in fact, even stranger than that. Consider this statement: “The function log x eventually increases more slowly than x^0.001, or x^0.00001, or x^0.0000001, or….” Suppose I raise this whole statement to some power—say, the hundredth power. (This is not a very rigorously mathematical procedure, I admit, but it gives a true result.) Applying Power Rule 3, the statement will then read: “The function (log x)¹⁰⁰ eventually increases more slowly than x^0.1, or x^0.001, or x^0.00001, or….” In other words, since log x increases more slowly than any power of x, the same is true of any power of log x. Each one of the functions (log x)², (log x)³, (log x)⁴, …, (log x)¹⁰⁰, …, increases more slowly than any power of x. Any power of log x eventually increases more slowly than any power of x. The graph of (log x)^N will eventually drop below, and for ever after stay below, the graph of x^ε , no matter how big N is or how small ε is.

This is hard to visualize. Those functions (log x)^N increase fast, and then very fast. Still, if you go far enough out to the east in Figure 5-3, every one of them will eventually, at some argument of stupendous size, drop below the x^0.3 curve, the x^0.2 curve, the x^0.1 curve, and any other curve of this family you might care to draw. You need to go

out east to the neighborhood of x = 7.9414 × 10³⁹⁵⁹ before (log x)¹⁰⁰ drops below the x^0.1 curve; but eventually it does.

V. Some of this I am going to use right away; some I shall leave lying here for future reference. All of it is important to the understanding of the Riemann Hypothesis, and I urge you to try out some of the main points, to check your understanding of them, before proceeding. A pocket calculator is good for this. You might, for example, find log 2 (which is 0.693147…) and log 3 (which is 1.098612…) and confirm that by adding them together you do indeed get log 6 (which is 1.791759…). Please notice, however, that because of the older use for base-10 logs that I mentioned, the “log” key on many pocket calculators delivers log to base 10. For the only log I care about, log to base e, such calculators generally provide an alternative key labeled “ln.” That’s the key you need. (The “n” stands for “natural”; log to base e is properly called “the natural log.”)

Now, let’s return to the Basel problem.

VI. As an illustration of what I said in section I about the search for closed-form solutions yielding important insights, Euler’s solution of the Basel problem not only gave a closed form for the reciprocal-squares series; as a by-product, it also gave closed forms for , , and so on. So long as N is an even number, Euler’s result tells you the precise value, as a closed form, of the infinite series shown in Expression 5-1.

Expression 5-1

When N is 2, the series converges on π²/6, as I said. When N is 4, it converges on π⁴/ 90; when N is 6 it converges on π⁶/945, and so on. Euler’s argument provided an answer for every even number N. He himself, in a later publication, took the argument all the way out to N = 26, when the series converges to 1315862π²⁶ / 11094481976030578125.

But what if N is odd? Euler’s result has nothing to say about that. Neither has any other result in the 260-odd years since. We have no clue about the closed form for , if there even is one, nor the equivalent for any other odd number. Nobody has been able to find closed forms for these series. We know that they converge, and we can of course, by brute calculation, get their values to any required degree of accuracy. We just don’t know what they mean. They are, in fact, very difficult numbers. It was not until 1978 that was even proved irrational.²⁸

So by the middle of the eighteenth century, quite a lot of mathematicians were thinking about the infinite series in Expression 5-1. Precise values—closed forms—were known for all even numbers N, while for the odd numbers, approximate values could be got by just adding up enough terms. Remember that when N is 1, the series is just the harmonic series, which diverges. Table 5-1 shows values for Expression 5-1—which, just to remind you, is

(to 12 decimal places). This looks like one of those snapshots of a function that I spoke about in Chapter 3.iv. Sure enough, it is. Recall the statement of the Riemann Hypothesis that I gave in my Prologue.

The Riemann Hypothesis

All non-trivial zeros of the zeta function have real part one-half.

Table 5-1 is your first glimpse of Riemann’s zeta function, and therefore a first step toward understanding the Riemann Hypothesis.

VII. Since, in the earlier sections of this chapter, I went to the trouble of defining the meaning of “x^a” for any number a, not just whole numbers, I am under no obligation to restrict the number N in Expression 5-1 to whole numbers. I can, in my imagination, let it roam freely over fractions, negative numbers, and irrational numbers. There is no guarantee that the infinite series will converge for all numbers—we already know from Chapter 1.iii that it doesn’t when N = 1. But we can at least entertain the possibility.

In honor of this new realization, I am going to change the “N” to a different letter, one that has less traditional association with whole numbers. The obvious choice is, of course, “x.” Riemann himself, however, did not use “x” in his 1859 paper. These matters were not so settled in his day. He used “s” instead; and so momentous was that 1859 paper that every succeeding mathematician has followed him. In studies of the zeta function, the argument is always given as “s.”

Here then, at last, is the Riemann zeta function (zeta, written “ζ ,” being the sixth letter of the Greek alphabet).

Expression 5-2

VIII. Before going any further, let me introduce a handy mathematical notation that cuts down on typing. (Do you think it’s easy, getting stuff like Expression 5-2 into Microsoft Word?)

If mathematicians want to add up a lot of terms that all have the same pattern, they use the Σ sign. That’s a capital sigma, the eighteenth letter of the Greek alphabet, the Greek “s” (for “sum”). The way it works is, you stick the pattern “under” (which actually means to the right, though we illogically say “under”) the sigma sign. Then at bottom and top of the sigma, you declare where your sum will start and end. This expression, for example,

is mathematicians’ shorthand for . The sigma says “add ’em up”; the expressions at the top and bottom of the sigma tell us when to start and when to finish adding; and the expression “under” (to the right of) the sigma tells us what, exactly, is being added—in this case, .

Mathematicians are not especially strict about the style of these expressions. That one, for example, would probably be written

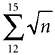
since it is obvious that it must be “n” that’s going from 12 to 15. Now, using the sigma sign, I can save myself a lot of fiddling around with symbols by rewriting Expression 5-2 as

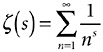
Or equivalently, bearing in mind Power Rule 5,

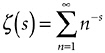
In fact, since “n” is so commonly and obviously used to stand for the positive whole numbers 1, 2, 3, 4, …, mathematicians are generally even more terse, just writing

which, again, is Riemann’s zeta function. This is pronounced “Zeta of s is defined to be the sum over all n of n to the power of minus s.” Here, “all n” is understood to mean “all positive whole numbers n.”

IX. Having got the zeta function set up as a neat expression, let’s turn our attention to that argument “s.” We know, from Chapter 1.iii, that when s is 1, the series diverges, so that the zeta function has no value. When s is 2, 3, 4, … it always converges, though, and we get values for the zeta function (see Table 5-1). In fact, you can show that the series converges for any number bigger than 1. When s is 1.5, it converges to 2.612375…. When s is 1.1, it converges to 10.584448…. When s is 1.0001 it converges to 10,000.577222…. It might seem odd that the series diverges when s = 1 but yet manages to converge for s = 1.0001. This is a common situation in math, though. In fact, when s gets very close to 1, the zeta function behaves remarkably like 1 / (s – 1). This, too, has a value for any number s except when s is precisely equal to 1, because the denominator is then zero, and you can’t divide by zero.

Perhaps a graph will make things clearer. Figure 5-4 is a graph of the zeta function. You can see that as s approaches the number 1 from the right, the function value shoots up to infinity; and as s itself goes off to infinity at the far right, the function value gets closer and closer to 1. (I’ve drawn in the line s = 1 and the constant function 1, both dashed.)

The graph doesn’t show any part of the function to the left of the line s = 1. That’s because so far I’ve been assuming that s is greater

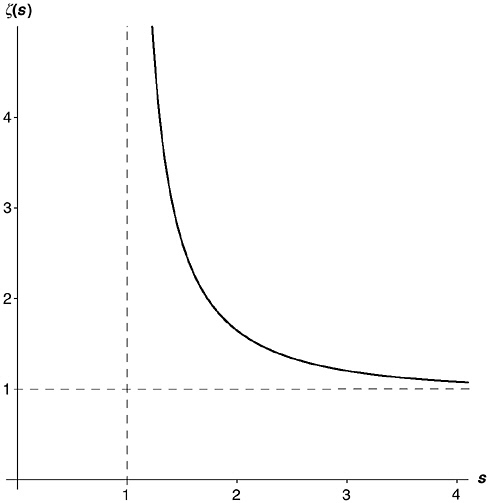
FIGURE 5-4 The zeta function, for arguments greater than 1.

than 1. What if it isn’t? What if, for example, s is zero? Well, then Expression 5-3 would look like this:

By Power Rule 4, this sum is 1 + 1 + 1 + 1 + 1 + 1 +…, which pretty obviously diverges. Add a hundred terms, the sum is a hundred; add a thousand, the sum is a thousand; add a million, the sum is a million. Yep, it diverges.

For negative numbers, things are even worse. What value does Expression 5-2 have if x is –1? From Power Rule 5, 2^–1 is just , 3^–1 is

just , and so on. Since is just 2, is just 3, etc., the series looks like this, 1 + 2 + 3 + 4 + 5 +…. Definitely divergent. How about ? Since is just etc., the series is

Since the square root of any whole number is smaller than the number, each term in this series is bigger than the corresponding term in (Basic algebra: if a is smaller than b, then 1/a is bigger than 1 / b. For example, 2 is smaller than 4, but is bigger than .) That series diverges, so this one must, too. Sure enough, if you take the trouble to actually work out the sums and add them up, you see that the first ten terms add up to 5.020997899…, the first hundred add up to 18.589603824…, the first thousand add up to 61.801008765…, the first ten thousand to 198.544645449…and so on.

It seems that the graph shows all that can be shown of the Riemann zeta function. There’s no more. The function has values only when s is greater than 1. Or, as we now know to say, using the proper term of art, the domain of the zeta function is all numbers greater than 1. Right? Wrong!