21
THE ERROR TERM
I. In Chapter 19, after defining that step function J in terms of the prime counting function π , I used Möbius inversion to get π in terms of J. Then, turning the Golden Key, I went through the steps Riemann took to express the zeta function ζ in terms of J. Another inversion (I said) will now give J in terms of ζ . The long and short of it is that:
-
The prime counting function π can be written in terms of another step function, J.
-
The function J can be written in terms of Riemann’s zeta function ζ .
It follows that all the properties of the prime counting function π are coded, in some way, in the properties of ζ . A sufficiently close study of ζ will tell us all we want to know about π —that is, about the distribution of prime numbers.
How does this actually work? What’s the code? Where do those non-trivial zeros come into it? And what does that middle-man
function, J, look like when written in terms of ζ —a point I left hanging at the end of Chapter 19?
II. I left it hanging for a very good reason, which will now become clear. Expression 21-1 shows the result of that last inversion, the final and precise expression for J(x) in terms of the zeta function.
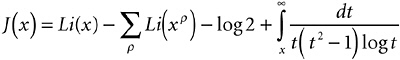
Expression 21-1
You take the point. If you’re not a mathematician, that’s an ugly beast of a thing (and where, by the way, is the zeta function in it?) I’m going to take it apart piece by piece, though, and show you what’s going on inside it. First, I just want you to know that this equation is the main result of Riemann’s 1859 paper. If you can get some kind of a handle on it, you will essentially understand Riemann’s work in this area and have a clear view of all that followed.
The first thing to note is that Expression 21-1 has four parts, or terms, on the right-hand side. The first term, Li(x), is generally called the “principal term.” The second term, ![]() , was referred to by Riemann in the plural as the “periodic terms” (periodischer Glieder) for reasons that will shortly become clear; I shall speak of it in the singular as the “secondary term.” The third term is a no-brainer. It’s just a number, log 2, which is 0.69314718055994….
, was referred to by Riemann in the plural as the “periodic terms” (periodischer Glieder) for reasons that will shortly become clear; I shall speak of it in the singular as the “secondary term.” The third term is a no-brainer. It’s just a number, log 2, which is 0.69314718055994….
The fourth term, though intimidating to the nonmathematician, is in fact easy to dispose of. It’s an integral, that is, the area under the curve of a certain function, from argument x all the way out to infinity. The function is, of course, 1 / (t(t2 – 1) log t). If you draw a graph of this function (see Figure 21-1), you will see that it is very friendly to the purpose in hand. Bear in mind that we have no interest in
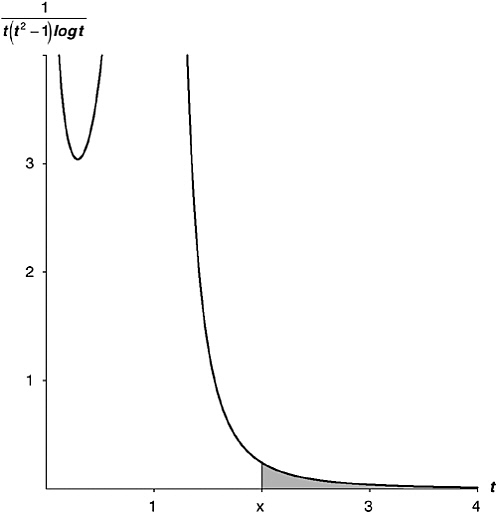
FIGURE 21-1 The fourth term of Riemann’s expression for J(x).
arguments x less than 2, since J(x) is zero when x is less than 2. So the shaded area I’ve shown, corresponding to x = 2, is as big as this integral—this fourth term—is ever going to get. The actual value of this area, the maximum value of the fourth term for any x we might ever be interested in, is, in fact, 0.1400101011432869….
So the third and fourth terms taken together (and minding signs) are limited to the range from –0.6931… to –0.5531…. Since we are studying π (x), which is only really interesting up in the millions and trillions, this is pretty inconsequential. I will, therefore, say almost nothing more about those last two terms and concentrate on the first two.
The principal term is not too much of a problem either. I have already defined the function Li(x) in Chapter 7.viii as the area under the curve of 1 / log t from zero to x, and I have given the Prime Number Theorem (PNT) in the form π (N)~Li(N). In this principal term, x is a real number. The value of Li(x) can, therefore, be looked up in a book of mathematical tables, or computed by any decent math software package like Maple or Mathematica.126
Having thus disposed of the first, third, and fourth terms in Expression 21-1, I will focus on the second, ![]() . This is the heart of the matter; this is the real business. First I will explain broadly what it means and how it got into Expression 21-1. Then I shall take it apart and show why it is crucial to understanding the distribution of primes.
. This is the heart of the matter; this is the real business. First I will explain broadly what it means and how it got into Expression 21-1. Then I shall take it apart and show why it is crucial to understanding the distribution of primes.
III. The Σ is an invitation to add many things together. The things to be added together are indicated by the little “ ρ ” underneath the sign. That’s not an American “p,” it’s a “rho,” the seventeenth letter of the Greek alphabet, and in this usage stands for “root.” To calculate this secondary term you must add up Li(xρ) for all of these roots, with ρ taking the value of one root after another. And what are these roots? Why, they are the non-trivial zeros of the Riemann zeta function!
How did these zeros turn up in the expression for J(x)? I can explain this, but only in outline. Recall the expression we arrived at in Chapter 19 by turning the Golden Key,
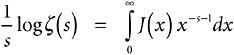
I said that mathematicians have a way to invert this, to turn it inside out, to get J(x) in terms of the zeta function. The actual process of inversion is rather long and complex (in both senses of that word!),
and most of the steps involve math beyond the level I am presenting here. That is why I have leaped straight to the final result, my Expression 21-1. I think I can explain one part of the process, though. It happens that one step in this inversion is to express the zeta function in terms of its zeros.
Expressing functions in terms of their zeros is not altogether a novel idea, if you have done high school algebra. Consider the good old quadratic equation, for example. I’ll take the one I used in Chapter 17.iv, z2 – 11z + 28 = 0 (but using z instead of x, since we are in the realm of complex numbers here). The left-hand side of this equation is of course a function, a polynomial function. If you feed in any argument z and do some arithmetic, it works out to some function value. If you feed in the argument 10, for example, the value is 100 – 110 + 28, which is 18. If you feed in the argument i, the value is 27 – 11i.
What are the solutions of the equation z2 – 11z + 28 = 0? As I showed in Chapter 17, the solutions are 4 and 7. If you feed either number into the function on the left-hand side, the equation is true, the left-hand side is equal to zero. Another way to say this is that 4 and 7 are the zeros of the function z2 – 11z + 28.
Now that I know the zeros, I can factorize this function. It factorizes to (z – 4)(z – 7); or what, by the rule of signs, amounts to the same thing, (4 – z)(7 – z). Another way to write this is 28(1 – z /4) (1 – z / 7). And, look! Either way, I have expressed the function z2 – 11z + 28 in terms of its zeros. This doesn’t work only for quadratic functions, of course. The fifth-degree polynomial z5 – 27z4 + 255z3 – 1045z2 + 1824z – 1008 can be rewritten in terms of its zeros (which are 1, 3, 4, 7, and 12), too. Here it is: –1008(1 – z / 1)(1 – z /3) (1 – z / 4)(1 – z / 7)(1 – z / 12). Any polynomial function can be rewritten in terms of its zeros.
From the point of view of complex function theory, polynomial functions have a very interesting property. The domain of a polyno-
mial is all complex numbers. A polynomial never “equals infinity.” There is no argument z for which its value just can’t be calculated. Calculating the value of a polynomial function for any given argument just involves raising the argument to natural-number powers, multiplying it by numbers, and adding the results together. You can do that with any number.
Functions whose domain is all complex numbers and which are decently well behaved (there is a precise mathematical definition of that!) are called entire functions. All polynomials are entire functions, so is the exponential function. Those rational functions I showed in Chapter 17.ii, however, are not entire functions, since their denominators can be zero. The log function is not an entire function, either: it has no value at argument zero. Riemann’s zeta function, likewise, has no value at argument 1, and so is not an entire function.
An entire function might have no zeros at all (like the exponential function: ez = 0 is never true), or it might have many (like a polynomial: 4 and 7 are the zeros of z2 – 11z + 28), or it might have infinitely many (like the sine function, which is zero at every integer multiple of π ).127 Now since polynomials can be rewritten in terms of their zeros, can all entire functions that have zeros be rewritten this way? Suppose I have some entire function, call it F, that can be defined by an infinite sum, F(z) = a + bz + cz2 + dz3 + …. And suppose I happen to know that this function has infinitely many zeros; call them ρ , σ , τ …. Can I rewrite this function in terms of its zeros, as an infinite product, F(x) = a (1 – z / ρ )(1 – z / σ )(1 – z / τ )…? As if the infinite sum were a sort of super-polynomial?
The answer is that under certain conditions, yes, you can. When you can do it, it’s often a very handy thing. This, for example, is how Euler solved the Basel problem, by applying this reasoning to the sine function.
How does this help us with the zeta function, which unfortunately is not an entire function? Well, as part of that complicated
inversion process, Riemann transformed the zeta function into something slightly different—an entire function, whose zeros are exactly the non-trivial zeros of the zeta function. At that point, we can write out this slightly different function in terms of those zeros. (The trivial zeros conveniently vanished during the transformation.)
That, after some further processing, is how we end up with ![]() , with the sum being taken over all the non-trivial zeros of the zeta function.
, with the sum being taken over all the non-trivial zeros of the zeta function.
Now, to show the significance of this second term in Expression 21-1, and the problems it raises, I am going to take it apart. I shall do this from the inside out, first looking at xρ , then at the Li function, and then at the matter of summing across all possible zeros ρ .
IV. I have this number x, which is a real number. (The ultimate object of the exercise is to get a formula for π (x), and π (x) is relevant only for real numbers—only for natural numbers, to tell the truth; but we have switched from “N” to “x” so that we can apply the tools of analysis.) I raise this real number x to the power of ρ , which is a complex number—one having the form ![]() , for some real number t, if the Riemann Hypothesis (RH) is true. This is worth a note by itself.
, for some real number t, if the Riemann Hypothesis (RH) is true. This is worth a note by itself.
If you raise a real number x to a complex power a + bi, the rules of complex arithmetic dictate the following. The modulus of the answer—how far it is from zero, as the crow flies—is xa. It is not affected by b at all. The amplitude of the answer—how far round it is, which part of the complex plane it is found in—depends on x and b. It is not affected by a.
If you raise a real number x to the power ![]() , the modulus of the result is, therefore, x to the power of
, the modulus of the result is, therefore, x to the power of ![]() , that is,
, that is, ![]() . The amplitude, however, might be anything at all—the result might be any-
. The amplitude, however, might be anything at all—the result might be any-
where in the complex plane, so long as its distance from zero is ![]() . To put it another way, if, for a given number x, you compute values of xρ for a host of different zeta zeros ρ, the numbers you get are scattered round the circumference of a circle of radius
. To put it another way, if, for a given number x, you compute values of xρ for a host of different zeta zeros ρ, the numbers you get are scattered round the circumference of a circle of radius ![]() in the complex plane, centered on zero. (If the RH is true!)
in the complex plane, centered on zero. (If the RH is true!)

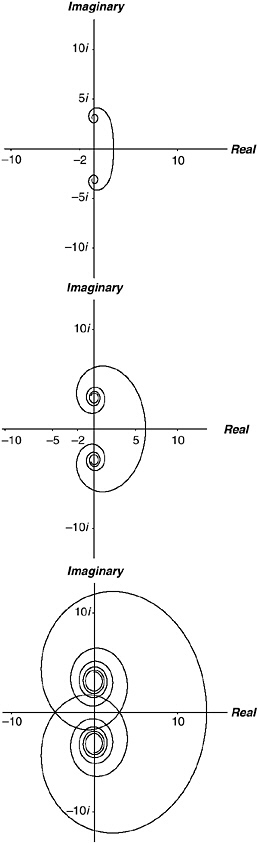
FIGURE 21-2 The value plane for the function w = 20z, showing the values of w for the first 20 non-trivial zeros of the zeta function.
The points marked on Figure 21-2 are the results of raising 20 to the power of the first, second, third, …, twentieth zeros of the zeta function. You see how the results are scattered around a circle of radius  (which is 4.47213…) in the complex plane, in no particu-
(which is 4.47213…) in the complex plane, in no particu-
lar order. This is because the function 20z sends the critical line into a circle radius ![]() , wrapping the critical line (and all the zeta zeros speckled along it) round and round that circle an infinity of times. Mathematically speaking, that circle in the value plane is 20critical line. If you imagine our pal the argument ant walking north up the critical line in the argument plane with his function-ometer set to the function 20z, his twin brother, the value ant, tracing out the corresponding values in the value plane, is walking round and round and round that circle. He is proceeding counterclockwise and by the time the argument ant has reached the first zeta zero, the value ant is nearly three-quarters of the way through his seventh circuit.
, wrapping the critical line (and all the zeta zeros speckled along it) round and round that circle an infinity of times. Mathematically speaking, that circle in the value plane is 20critical line. If you imagine our pal the argument ant walking north up the critical line in the argument plane with his function-ometer set to the function 20z, his twin brother, the value ant, tracing out the corresponding values in the value plane, is walking round and round and round that circle. He is proceeding counterclockwise and by the time the argument ant has reached the first zeta zero, the value ant is nearly three-quarters of the way through his seventh circuit.
V. Now, one by one, I am going to find the Li function of all those points—the whole infinity of them. Unfortunately, they are complex numbers. I defined the Li function only for real numbers, as the area under a curve. Is there a way to define Li for complex numbers, too? How do integrals work with complex numbers? Yes, there is a way to define it; and, yes, there is a way to develop integrals involving complex numbers. Integration is in fact a key feature of complex analysis, the subject of many of the most beautiful and powerful theorems in the topic. I shall not go into detail, only say that, yes, Li(z) is defined128 for complex numbers z.
Figure 21-3 shows where the first 10 of the points in Figure 21-2 are sent by the Li function. To put it another way, it shows where the critical line (to be precise, a stretch of it from ![]() to
to ![]() ) is sent by the function Li(20z). As you can see, this function maps the critical line into a counter-clockwise spiral that closes in on the number π i as the argument ascends the critical line. Where the function 20z wrapped the critical line infinitely many times round and round the circle with radius
) is sent by the function Li(20z). As you can see, this function maps the critical line into a counter-clockwise spiral that closes in on the number π i as the argument ascends the critical line. Where the function 20z wrapped the critical line infinitely many times round and round the circle with radius ![]() , applying the Li function unwraps it into this elegant spiral, with the zeros still dotted along it.
, applying the Li function unwraps it into this elegant spiral, with the zeros still dotted along it.
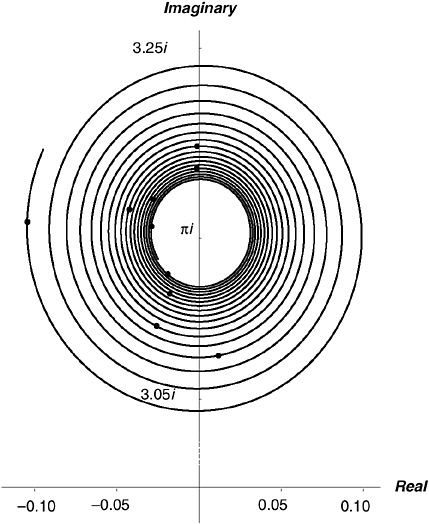
FIGURE 21-3 The function Li(20z) for a segment of the critical line.
VI. Now I shall tackle the sigma sign—the business of summing those dots (each of which is just a complex number) across all possible non-trivial zeros of the zeta function. To do this, let me first bring up a point I have mostly been ignoring so far. For any non-trivial zero on the north half of the critical line, there is a corresponding one in the south half. That is, if ![]() is a zero of the zeta function, so must
is a zero of the zeta function, so must ![]() be. In proper math language, if z is a zero, then so is its complex conjugate
be. In proper math language, if z is a zero, then so is its complex conjugate ![]() . (Remember that “
. (Remember that “ ![]() ” is pronounced “z-bar.” At this point you might want to check back with Figure 11-1 to refresh your memory on complex number basics.)
” is pronounced “z-bar.” At this point you might want to check back with Figure 11-1 to refresh your memory on complex number basics.)
In carrying out this summation, the south half of the critical strip plays a key role. Figures 21-2 and 21-3 were concerned only with the first few zeros along the northern half of the critical line. For a fuller picture, including the southern half of the line, Figure 21-4 shows, at the far left, a plane of complex numbers with the critical strip marked in from ![]() to
to ![]() . This is enough to show the first zero at
. This is enough to show the first zero at ![]() , and also its complex conjugate at
, and also its complex conjugate at ![]() . I have marked them as “ ρ ” and “
. I have marked them as “ ρ ” and “![]() .”
.”
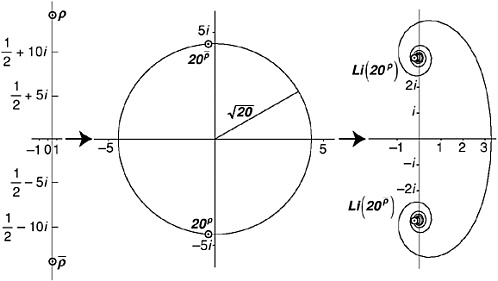
FIGURE 21-4 The critical line, out to the first pair of non-trivial zeros, mapped first by the function 20z, then by the function Li(20z).
Taking this as the argument plane for the function 20z, the middle part of the diagram shows the “comes from” figure in the value plane, a circle of radius ![]() , with 20ρ marked as in Figure 21-2, and now also
, with 20ρ marked as in Figure 21-2, and now also ![]() . Notice that the values are complex conjugates just as the arguments are. This doesn’t happen with all functions, but fortunately it does with 20z. If we apply the Li function, using that middle figure this time as the argument plane for Li, we see that the critical line, which got wound round that circle an infinity of times by 20z, now unwinds into that pleasing double spiral at the right. (Figure 21-3 was a close-up of the top spiral.) And again, when the arguments are complex conjugates, so are the values.
. Notice that the values are complex conjugates just as the arguments are. This doesn’t happen with all functions, but fortunately it does with 20z. If we apply the Li function, using that middle figure this time as the argument plane for Li, we see that the critical line, which got wound round that circle an infinity of times by 20z, now unwinds into that pleasing double spiral at the right. (Figure 21-3 was a close-up of the top spiral.) And again, when the arguments are complex conjugates, so are the values.
There is just one more thing to notice before I actually evaluate the sum ![]() . That spiral—Figure 21-3 shows it best—isn’t closing in on its target very fast. Its closing-in rate is, in fact, harmonic. That is, if you imagine the argument ant walking north up the critical line with his function-ometer set to Li(20z), the value ant traversing the spiral in the value plane is getting closer and closer to π i at a rate inversely proportional to the argument ant’s height. If the argument ant’s height is T, the value ant’s distance from π i is (roughly) proportional to 1 / T.
. That spiral—Figure 21-3 shows it best—isn’t closing in on its target very fast. Its closing-in rate is, in fact, harmonic. That is, if you imagine the argument ant walking north up the critical line with his function-ometer set to Li(20z), the value ant traversing the spiral in the value plane is getting closer and closer to π i at a rate inversely proportional to the argument ant’s height. If the argument ant’s height is T, the value ant’s distance from π i is (roughly) proportional to 1 / T.
Bearing this in mind, I am now ready to tackle the sum ![]() . What I am adding is the complex numbers that correspond to all those dots on the spiral in Figure 21-3, together with all the complex conjugate dots on the southern spiral. Since for every dot on the northern spiral there is a mirror-image dot in the southern one, the imaginary parts all cancel out. Every a + bi has a corresponding a – bi, so when I add them I just get 2a. This is just as well because J(x) is a real number. It wouldn’t do to have imaginary numbers showing up on the right-hand side of Expression 21-1! It is really good news, in fact, because it means I have to add up only the real (that is, east-west) parts of the dots in Figure 21-3. The contribution of the southern hemisphere is merely to double the answer, (a + bi) + (a – bi) = 2a.
. What I am adding is the complex numbers that correspond to all those dots on the spiral in Figure 21-3, together with all the complex conjugate dots on the southern spiral. Since for every dot on the northern spiral there is a mirror-image dot in the southern one, the imaginary parts all cancel out. Every a + bi has a corresponding a – bi, so when I add them I just get 2a. This is just as well because J(x) is a real number. It wouldn’t do to have imaginary numbers showing up on the right-hand side of Expression 21-1! It is really good news, in fact, because it means I have to add up only the real (that is, east-west) parts of the dots in Figure 21-3. The contribution of the southern hemisphere is merely to double the answer, (a + bi) + (a – bi) = 2a.
The rest of the news is not so good. The dots scattered along that spiral in Figure 21-3 are, as I observed, closing in on π i—their real parts, therefore, closing in on zero—at a harmonic rate. Adding up the real parts of all those dots, therefore, offers the danger that I might be adding up something like the harmonic series, which, we recall from Chapter 1, is divergent. How do I know this sum ![]() converges?
converges?
It helps that the dots can have real parts that are either positive or negative. In fact, the sum this one resembles is not the harmonic sum but its cousin, which I introduced briefly in Chapter 9.vii:
Here the terms approach zero harmonically: ![]() but the alternating plus and minus signs mean that each term to some degree cancels out the term before, and convergence is possible. However, the convergence is, in the terminology I introduced in Chapter 9.vii, only conditional. It depends on adding up the terms in the correct order.
but the alternating plus and minus signs mean that each term to some degree cancels out the term before, and convergence is possible. However, the convergence is, in the terminology I introduced in Chapter 9.vii, only conditional. It depends on adding up the terms in the correct order.
Just so with ![]() . We need to be careful about the order in which we do the addition if we want to be sure of convergence to the correct number. So what is the proper order? It is just what you would think it should be. Take the zeros one by one, heading north up the critical line, pairing off each zero with its complex-conjugate zero down south.
. We need to be careful about the order in which we do the addition if we want to be sure of convergence to the correct number. So what is the proper order? It is just what you would think it should be. Take the zeros one by one, heading north up the critical line, pairing off each zero with its complex-conjugate zero down south.
VII. So to evaluate ![]() we first pair off each zeta zero with its mirror image (i.e., complex conjugate) in the south half of the argument plane. Then these pairs must be taken in ascending order of the positive imaginary parts. So we take the zeros in this order,
we first pair off each zeta zero with its mirror image (i.e., complex conjugate) in the south half of the argument plane. Then these pairs must be taken in ascending order of the positive imaginary parts. So we take the zeros in this order,

To see how this process actually works out, and to get an insight into why Riemann called this secondary term the “periodic terms,” let me work through the arithmetic for an actual value of x. I’ll take x = 20 as before, so we are engaged in computing J(20)—which, you can easily
verify from the original definition of J, is actually ![]() , that is, 9.5833333…. Here goes.
, that is, 9.5833333…. Here goes.
First, I must raise 20 to the power ![]() . The result is –0.302303 – 4.46191i, which is the dot marked “1” in Figure 21-2. Take the logarithmic integral—the Li function—of that to get the answer –0.105384 + 3.14749i, which is the western-most dot in Figure 21-3. Now do the conjugate member of this pair of zeros. Raise 20 to the power
. The result is –0.302303 – 4.46191i, which is the dot marked “1” in Figure 21-2. Take the logarithmic integral—the Li function—of that to get the answer –0.105384 + 3.14749i, which is the western-most dot in Figure 21-3. Now do the conjugate member of this pair of zeros. Raise 20 to the power ![]() . The result is –0.302303 + 4.46191i. That’s shown in the middle picture of Figure 21-4. It’s the mirror image in the real axis of the “1” dot in Figure 21-2. Take the logarithmic integral to get answer –0.105384 – 3.14749i, which is the one way down south on the right of Figure 21-4. Add the two answers: –0.210768. The imaginary parts have, of course, canceled out. So much for the first matching pair of zeros.
. The result is –0.302303 + 4.46191i. That’s shown in the middle picture of Figure 21-4. It’s the mirror image in the real axis of the “1” dot in Figure 21-2. Take the logarithmic integral to get answer –0.105384 – 3.14749i, which is the one way down south on the right of Figure 21-4. Add the two answers: –0.210768. The imaginary parts have, of course, canceled out. So much for the first matching pair of zeros.
Repeat for the second pair, ![]() and
and ![]() . The final answer this time is 0.0215632. For the third pair it’s –0.0535991. Three down, an infinity to go!
. The final answer this time is 0.0215632. For the third pair it’s –0.0535991. Three down, an infinity to go!
After 50 of these calculations, you have the following answers (read down the columns):
|
–0.210768 |
0.0563226 |
–0.0332852 |
0.00801349 |
0.0240114 |
|
0.0215632 |
–0.0274298 |
–0.00692417 |
0.0279464 |
–0.0223427 |
|
–0.0535991 |
0.0481966 |
0.0205354 |
0.0159041 |
–0.0225924 |
|
–0.00432174 |
0.00127986 |
–0.0312052 |
–0.0102871 |
–0.000132221 |
|
–0.0868451 |
0.0128283 |
0.0280167 |
0.0224912 |
–0.0180932 |
|
–0.037716 |
–0.00472225 |
0.0188243 |
–0.00106082 |
0.0221559 |
|
–0.0046281 |
0.0361164 |
0.0228139 |
0.0130158 |
–0.017333 |
|
–0.0577894 |
0.0317626 |
–0.0301646 |
–0.0191586 |
–0.0150514 |
|
–0.0400277 |
0.0222196 |
0.0208943 |
–0.018169 |
0.0206192 |
|
–0.0595976 |
–0.037927 |
0.0275883 |
–0.0165671 |
0.0207551 |
That first is a bit of an anomaly, because that westernmost dot in Figure 21-3 is more than twice as far from the vertical axis as any of the others. After that, though, they get smaller as the values corresponding to the north half of the critical line spiral in toward π i.
And look at the signs—there are about as many positives as negatives.129 That’s good news, because, though the answers are getting smaller, they’re not getting smaller very fast, and we need all the help we can get from positives and negatives canceling each other out on addition. This is all happening under the sigma sign, remember— those 50 numbers have to be added up. (The sum is –0.343864, which is, as a matter of fact, within 8 percent of the infinite sum. Not bad for just 50 terms.)
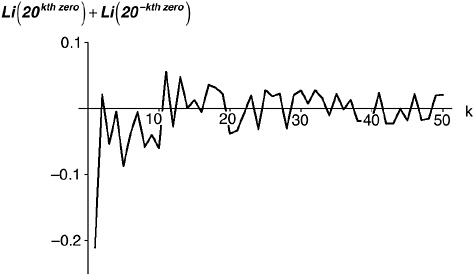
FIGURE 21-5 The first 50 values got by taking a non-trivial zero and its complex conjugate, computing the function values Li (20z), and then adding them.
You can see from Figure 21-5 why Riemann referred to these components of the secondary term as “periodic.” They vary irregularly (which means, if you want to be finicky about it, that they are not strictly “periodic,” only “oscillatory”) up and down, from positive to negative and back.130 The reason for this is plain in Figure 21-3.
The oscillatory quality of these secondary terms arises because, as Figure 21-3 shows, the function Li(xρ) winds the critical line round and round in an ever-tighter spiral. The function values for the zeros are likely to end up anywhere on this spiral; especially since, for large x, the critical line gets immensely stretched before being wound. The winding is so tight that a high segment of the critical line maps into
something very close to a circle. The values for the zeros, therefore, resemble points scattered around the circumference of a circle again. If you know some trigonometry, you know that this brings us into the world of sines and cosines, of wave functions, oscillations, vibrations … of music. This is the ultimate root of Sir Michael Berry’s notion of the “music of the primes.”

FIGURE 21-6 Same as Figure 21-5, but showing 1,000 values (and the points not joined up).
As you add them up, the terms are gradually decreasing, and the positives and negatives are canceling out, and you get convergence, though it’s awfully slow. For three-digit accuracy you need to add up over 7,000 terms; for four-digit accuracy, more than 86,000. In Figure 21-6 I have plotted the first 1,000 results (though some over at the left got lost in the scaling) without attempting to join the dots this time. You can see that they really do get smaller, though at a leisurely pace.
The final result is –0.370816425…. This is, to remind you, the second term in Expression 21-1. The first is, in this case, Li(20), which is 9.90529997763…. The third term is log 2, which is 0.69314718055994…. The fourth term, that nuisance integral, deliv
ers a piddling 0.000364111…. Feed those into Expression 21-1 and— ker-ching! J(20) = 9.58333333, which we knew all along.
VIII. I’ll round off with a complete calculation of π (1,000,000), the number of primes up to one million, using Riemann’s formula— not for the fun of it, though it is of course great fun, but to make some important points about the error term.
Remember from Chapter 19.iv that
How far do I need to take that right-hand side? Until the number inside the parenthesis is less than 2, because J(x) is zero when x is less than 2. The nineteenth root of 1,000,000 is 2.069138…; the twentieth root is 1.995262…. We can, therefore, stop at 19. Since 19 is square-free and has only one prime factor—itself—the Möbius function μ (19) has value –1. The last item on the right-hand side is, therefore, ![]() . Altogether there are 13 items on that right-hand side since there are 13 numbers from 1 to 19 whose Möbius function is not zero: 1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19. The Möbius function is zero, remember, for any number that is divisible by a perfect square like 4 or 9.
. Altogether there are 13 items on that right-hand side since there are 13 numbers from 1 to 19 whose Möbius function is not zero: 1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19. The Möbius function is zero, remember, for any number that is divisible by a perfect square like 4 or 9.
Each of those 13 items has four terms: the principal term, the secondary term (which involves the zeros of the zeta function), the log 2 term, and the integral term. If I add up all 52 of these fragments, I have π (1,000,000)—which, we know in advance from Chapter 3.iii, is 78,498.
I have laid out all this arithmetic in Table 21-1 (omitting row N when μ (N) is zero). Reading across row N, and using y to stand for the N-th root of one million, the principal term is (μ (N) / N ) Li(y),
the secondary term is 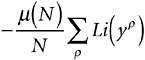 , the log 2 term is
, the log 2 term is  , and the integral term is
, and the integral term is 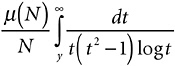 .
.
TABLE 21-1 Calculation of π (1,000,000).
|
N |
Principal term |
Secondary term |
Log 2 term |
Integral term |
Row totals |
|
1 |
78627.54916 |
–29.74435 |
–0.69315 |
0.00000 |
78597.11166 |
|
2 |
–88.80483 |
0.11044 |
0.34657 |
0.00000 |
–88.34782 |
|
3 |
–10.04205 |
0.29989 |
0.23105 |
0.00000 |
–9.51111 |
|
5 |
–1.69303 |
0.08786 |
0.13863 |
–0.00012 |
–1.46667 |
|
6 |
1.02760 |
–0.02349 |
–0.11552 |
0.00031 |
0.88889 |
|
7 |
–0.69393 |
–0.04737 |
0.09902 |
–0.00058 |
–0.64286 |
|
10 |
0.29539 |
–0.02791 |
–0.06931 |
0.00183 |
0.20000 |
|
11 |
–0.23615 |
–0.00634 |
0.06301 |
–0.00234 |
–0.18182 |
|
13 |
–0.15890 |
0.03206 |
0.05332 |
–0.00340 |
–0.07692 |
|
14 |
0.13281 |
–0.01581 |
–0.04951 |
0.00394 |
0.07143 |
|
15 |
0.11202 |
–0.00362 |
–0.04621 |
0.00448 |
0.06667 |
|
17 |
–0.08133 |
–0.01272 |
0.04077 |
–0.00554 |
–0.05882 |
|
19 |
–0.06013 |
–0.02241 |
0.03648 |
–0.00657 |
–0.05263 |
|
Column totals |
78527.34662 |
–29.37378 |
0.03515 |
–0.00799 |
78498.00000 |
The row totals should, and in fact do, work out to (μ (N) / N ) J(y). For an easy check, look at the row N = 6. Since a million is 106, the sixth root of a million is 10. The value of J(10) is easy to work out, it comes to ![]() . Because 10 is square-free and the product of two primes, its Möbius function μ (10) has the value +1. For the row N = 6, that last column should therefore work out to
. Because 10 is square-free and the product of two primes, its Möbius function μ (10) has the value +1. For the row N = 6, that last column should therefore work out to ![]() . That is
. That is ![]() , which is just what we have for the row total when N = 6.
, which is just what we have for the row total when N = 6.
The principal term when N = 1 is of course just Li(1,000,000), the approximation given by the PNT. What is the difference between that and π (1,000,000)? A quick subtraction gives the answer. The difference, taking it as π (1,000,000) minus Li(1,000,000) to preserve the signs in my table, is –129.54916. How is that difference made up? As follows.
|
From principal terms: |
–100.20254 |
|
From secondary terms: |
–29.37378 |
|
From log 2 terms: |
0.03515 |
|
From integral terms: |
–0.00799 |
The largest difference arises from the principal terms. However, these are pretty predictable. They decline steadily and rapidly.
The difference arising from the secondary terms is of the same order of magnitude, and its components, those secondary terms, are much more worrisome. The first secondary term is quite large and negative; but there is no obvious reason why this should be so. Even the others do not look helpful. If you just read down the column of secondary terms, ignoring minus signs, and noting whether each term is bigger or smaller than the one above it, they read: smaller, bigger, smaller, smaller, bigger, smaller, smaller, bigger, smaller, smaller, bigger, bigger. The one for N = 19 is almost as big as the one for N = 6. Those secondary terms, the terms that involve zeros of the zeta function, are the wild cards in this calculation. The log 2 and integral terms are, as I promised, negligible.
Think of Littlewood’s 1914 paper (Chapter 14.vii), in which he proved it is not true that Li(x) is always greater than π (x). That means that the difference will eventually be positive. Since the primary terms decrease very fast in size, and since the Möbius function makes most of the first few, including the really big ones (N = 2, N = 3, N = 5), negative, it’s hard to see how those primary terms can ever contribute anything to the difference but a big negative number. If the net difference is going to be positive, as Littlewood proved it eventually will be, then that number will have to be swamped by bigger, positive, sec-
ondary terms. For that to happen, the secondary terms—the zeros of the zeta function—are going to have to seriously misbehave. Apparently they do.
IX. For further insights into the meaning of the error term, look back at that double spiral on the right of Figure 21-4. It is Li(xcritical line) when x = 20. The critical line—with, if the RH is true, all the zeta zeros speckled along it—is sent to that spiral by the function Li(20z). What happens if, instead of 20, we choose some larger value of x? What will the corresponding spirals look like?
Figure 21-7 gives the general idea. It shows Li(10critical line), Li(100critical line) and Li(1,000critical line). In all three cases I have mapped the same segment of the critical line, the segment from ![]() to
to ![]() . Notice the following things that happen as x goes from 10, to 100, to 1,000.
. Notice the following things that happen as x goes from 10, to 100, to 1,000.
-
The spirals get bigger. They still, however, converge on the same two points, –π i and π i.
-
The segment of the critical line that we are mapping, which has length 10 units, gets more and more stretched, winding more and more times round the result points at –π i and π i.
-
The top spiral and the bottom spiral approach each other, “kiss” at some value of x between 100 and 1,000, and thereafter overlap. (The spirals actually kiss when x = 399.6202933538….)
The segment of the critical line I have mapped here is too short to reach to the first pair of zeros at ![]() . Because the line is getting stretched, wound more and more round the result points, even as the spirals get bigger, an interesting question arises. Does the stretching and winding perhaps keep the zeta zeros close in to –π i and π i, regardless of how big the spirals become? Answer: No, for
. Because the line is getting stretched, wound more and more round the result points, even as the spirals get bigger, an interesting question arises. Does the stretching and winding perhaps keep the zeta zeros close in to –π i and π i, regardless of how big the spirals become? Answer: No, for
bigger and bigger x, the zeta zeros map into points that get arbitrarily large. When ρ is the first zeta zero, the one at ![]() , for arguments x around a mere trillion, Li(xρ) is clocking up real parts of more than 2,200.
, for arguments x around a mere trillion, Li(xρ) is clocking up real parts of more than 2,200.
In Chapter 14.vii I noted the recent result by Bays and Hudson that the first Littlewood violation—when π (x) exceeds Li(x) for the first time—occurs before, and quite likely at, x = 1.39822 × 10316. Suppose I were to repeat the process I used to calculate π (1,000,000), but using this number—I’ll call it the “Bays-Hudson Number”—instead of 1,000,000. What would the arithmetic look like?
Obviously I would have more than 13 J-functions to work out. The 1,050th root of the Bays-Hudson number is 2.0028106…, the 1,051st root is 1.99896202…, so I must take first, second, …, 1,050th roots of the number and compute their J-functions. It’s not quite that bad, because a lot of the numbers from 1 to 1,050 are square-divisible, and so have Möbius function zero. How many? As a matter of fact 411, so I need to compute only 639 J-functions.131
The double spirals in Figure 21-7 cross the positive real axis successively further east, at 2.3078382, 6.1655995, and 13.4960622. If I was working with the Bays-Hudson Number, that double spiral would cross the real axis at a number much larger than these, a number that begins “325,771,513,660” and continues for a further 144 digits before reaching its decimal point. The spirals now are inconceivably vast. Yet they still close in on π i and –π i. This means that the top and bottom spirals massively overlap—you would not be able to distinguish them in a diagram. The critical line, with the zeros speckled along it (if the RH is true!) is tremendously stretched out. The diagram equivalent to Figure 21-3 has a far bigger hole in the middle— though still centered on π i—and the spiral winds trillions of times between successive low-order zeros, scrambling their coordinates in the complex plane very effectively, the real parts of the values oscillating between hugely negative and hugely positive numbers. And all this refers only to the first of the 639 table rows I need for computing π (Bays-Hudson Number). Those secondary terms are very unruly.
All of the calculations in this chapter have assumed, with occasional reminders, that the RH is true. If it is not true, then these elegant circles and spirals are mere approximations, and at some unknown height up the critical line—for some zero ρ far out along the infinite sum in that secondary term—the logic of this chapter falls apart. In the theory of the error term, the RH is central.
X. I have attained the main object of the mathematics in this book, to show the intimate connection between the distribution of prime numbers, as embodied in π (x), and the non-trivial zeros of the zeta function, which make up a large—and, by Littlewood’s result, sometimes dominant—component of the difference between π (x) and Li(x), that is, of the error term in the PNT.
All this was revealed to us by Bernhard Riemann’s dazzling 1859 paper. We know much more today, of course, than we did in 1859. Yet the great conundrum first set out in that paper still stands unresolved, as resistant to assaults by the world’s finest minds as when Riemann recorded his own “fleeting vain attempts” to prove it, back when analytic number theory had just been born. What are the prospects now, in the fifteenth decade of our efforts to crack the RH?