1
CARD TRICK
I. Like many other performances, this one begins with a deck of cards.
Take an ordinary deck of 52 cards, lying on a table, all four sides of the deck squared away. Now, with a finger slide the topmost card forward without moving any of the others. How far can you slide it before it tips and falls? Or, to put it another way, how far can you make it overhang the rest of the deck?
FIGURE 1-1
The answer, of course, is half a card length, as you can see in Figure 1-1. If you push it so that more than half the card overhangs, it falls. The tipping point is at the center of gravity of the card, which is halfway along it.
Now let’s go a little further. With that top card pushed out half its length—that is, to maximum overhang—over the second one, push that second card with your finger. How much combined overhang can you get from these top two cards?
The trick is to think of these top two cards as a single unit. Where is the center of gravity of this unit? Well, it’s halfway along the unit, which is altogether one and a half cards long; so it’s three-quarters of a card length from the leading edge of the top card (see Figure 1-2). The combined overhang is, therefore, three-quarters of a card length. Notice that the top card still overhangs the second one by half a card length. You moved the top two cards as a unit.
FIGURE 1-2
If you now start pushing the third card to see how much you can increase the overhang, you find you can push it just one-sixth of a card length. Again, the trick is to see the top three cards as a single unit. The center of gravity is one-sixth of a card length back from the leading edge of the third card (see Figure 1-3).
FIGURE 1-3
In front of this point is one-sixth of the third card, a sixth plus a quarter of the second card, and a sixth plus a quarter plus a half of the top card, making a grand total of one and a half cards.
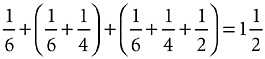
FIGURE 1-4
That’s half of three cards—the other half being behind the tipping point. Here’s what you have after pushing that third card as far as it will go (see Figure 1-4).
The total overhang now is a half (from the top card) plus a quarter (from the second) plus a sixth (from the third). This is a total of eleven twelfths of a card. Amazing!
Can you get an overhang of more than one card? Yes you can. The very next card—the fourth from the top—if pushed forward carefully, gives another one-eighth of a card length overhang. I’m not going to do the arithmetic; you can trust me, or work it out as I did for the first three cards. Total overhang with four cards: one-half plus one-quarter plus one-sixth plus one-eighth, altogether one and one-twenty-fourth card lengths (see Figure 1-5).
FIGURE 1-5
If you keep going the overhangs accumulate like this.
for the 51 cards you push. (No point pushing the very bottom one.) This comes out to a shade less than 2.25940659073334. So you have a total overhang of more than two and a quarter card lengths! (See Figure 1-6.)
FIGURE 1-6
I was a college student when I learned this. It was summer vacation and I was prepping for the next semester’s work, trying to get ahead of the game. To help pay my way through college I used to spend summer vacations as a laborer on construction sites, work that was not heavily unionized at the time in England. The day after I found out about this thing with the cards I was left on my own to do some clean-up work in an indoor area where hundreds of large, square, fibrous ceiling tiles were stacked. I spent a happy couple of hours with those tiles, trying to get a two and a quarter tile overhang from 52 of them. When the foreman came round and found me deep in contemplation of a great wobbling tower of ceiling tiles, I suppose
his worst fears about the wisdom of hiring college students must have been confirmed.
II. One thing mathematicians like to do, and find very fruitful, is extrapolation—taking the assumptions of a problem and stretching them to cover more ground.
I assumed in the above problem that we had 52 cards to work with. We found that we could get a total overhang of better than two and a quarter cards.
Why restrict ourselves to 52 cards? Suppose we had more? A hundred cards? A million? A trillion? Suppose we had an unlimited supply of cards? What’s the biggest possible overhang we could get?
First, look at the formula we started to develop. With 52 cards the total overhang was
Since all the denominators are even, I can take out one-half as a factor and rewrite this as
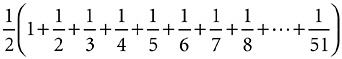
If there were a hundred cards, the total overhang would be
With a trillion cards it would be
That’s a lot of arithmetic; but mathematicians have shortcuts for this kind of thing, and I can tell you with confidence that the total overhang with a hundred cards is a tad less than 2.58868875882, while for a trillion cards it is a wee bit more than 14.10411839041479.
These numbers are doubly surprising. The first surprise is that you can get a total overhang of more than 14 full card lengths, even though you need a trillion cards to get it. Fourteen card lengths is more than four feet, with standard playing cards. The second surprise, when you start thinking about it, is that the numbers aren’t bigger. Going from 52 cards to 100 got us only an extra one-third of a card overhang (a bit less than one-third, in fact). Then going all the way to a trillion—a stack of a trillion standard playing cards would go most of the way from the Earth to the Moon—gained us only another 
card lengths.
And if we had an unlimited number of cards? What is the absolute biggest overhang we could get? The remarkable answer is, there is no limit. Given enough cards, you could have an overhang of any size. You want an overhang of 100 card lengths? You’d need a stack of about 405,709,150,012,598 trillion trillion trillion trillion trillion trillion cards—a stack whose height would far, far exceed the bounds of the known universe. Yet you could get still bigger overhangs, and bigger, as big as you want, if you’re willing to use unimaginably large numbers of cards. A million-card overhang? Sure, but the number of cards you need now is so huge it would need a fair-sized book just to print it in—it has 868,589 digits.
III. The thing to concentrate on here is that expression inside the parentheses
This is what mathematicians call a series, addition of terms continuing indefinitely, where the terms follow some logical progression. Here the terms 
are the reciprocals of the ordinary counting numbers 1, 2, 3, 4, 5, 6, 7, ….
The series 
is sufficiently important that mathematicians have a name for it. It is called the harmonic series.
What I have stated above amounts to this: by adding enough terms of the harmonic series, you can get a total as big as you please. The total has no limit.
A crude, but popular and expressive, way to say this is: the harmonic series adds up to infinity.
Well-brought-up mathematicians are taught to sniff at expressions like that; but so long as you know the pitfalls of using them I think they are perfectly all right. Leonhard Euler, one of the half-dozen greatest mathematicians who ever lived, used them all the time with very fruitful results. However, the proper mathematical term of art is: The harmonic series is divergent.
Well, I have said this, but can I prove it? Everybody knows that in mathematics you must prove every result by strict logic. Here we have a result: the harmonic series is divergent. How do you prove it?
The proof is, in fact, rather easy and depends on nothing more than ordinary arithmetic. It was produced in the late Middle Ages by a French scholar, Nicole d’Oresme (ca. 1323-1382). D’Oresme pointed out that 
is greater than 
; so is 
; so is 
; and so on. In other words, by taking 2 terms, then 4 terms, then 8, then 16 terms, and so on, you can group the series into an infinite number of blocks, every one of which is bigger than one-half. The entire sum must, therefore, be infinite. Don’t be perplexed by the fact that the blocks get bigger very quickly. There is an awful lot of room in “infinity,” and no matter how many blocks you take, the next block is well defined and waiting for you. There is always another one-half to be added; and that means that the total increases without limit.
D’Oresme’s proof of the divergence of the harmonic series seems to have been mislaid for several centuries. Pietro Mengoli proved the result all over again in 1647, using a different method; then, forty years later, Johann Bernoulli proved it using yet another method; and shortly after that, Johann’s elder brother Jakob produced a proof by a fourth method. Neither Mengoli nor the Bernoullis seem to have been aware of d’Oresme’s fourteenth-century proof, one of the barely known masterpieces of medieval mathematics. D’Oresme’s proof remains the most straightforward and elegant of all the proofs, though, and is the one usually given in textbooks today.
IV. The amazing thing about series is not that some of them are divergent, but that any of them are not. If you add together an infinity of numbers, you expect to get an infinite result, don’t you? The fact that you sometimes don’t can be easily illustrated.
Take an ordinary ruler marked in quarters, eighths, sixteenths, and so on (the more “so on” the better—I’ve shown a ruler marked in sixty-fourths). Hold a sharp pencil point at the very first mark on the ruler, the zero. Move the pencil one inch to the right. The pencil point is now on the one-inch mark and you have moved it a total of one inch (see Figure 1-7).
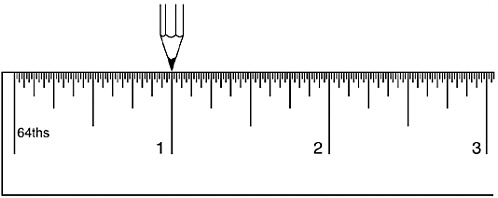
FIGURE 1-7
Now move the pencil half an inch further to the right (see Figure 1-8).
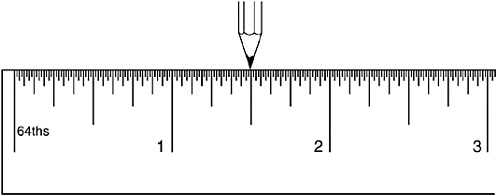
FIGURE 1-8
Now move the pencil a quarter-inch further to the right … then an eighth-inch … then a sixteenth … then a thirty-second … then a sixty-fourth. Your pencil is in the position shown in Figure 1-9
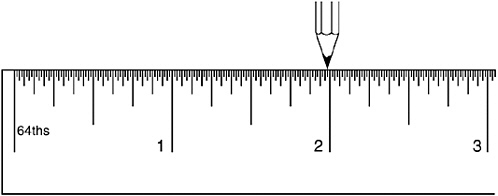
FIGURE 1-9
… and you have moved to the right a total distance of
which is, as you can see, 
. Clearly, if you could go on like this, halving the distance each time, you would get closer and closer to the two-inch mark. You would never quite reach it; but there is no limit
to how close you could get. You could get to within a millionth of an inch of it; or a trillionth; or a trillion trillion trillion trillion trillion trillion trillion trillion trillionth. We can express this fact as
Expression 1-1
where it is understood that there is an infinite number of terms to add up on the left-hand side of the equals sign.
The point I’m making here is the difference between the harmonic series and this new one. With the harmonic series I added up an infinite number of terms and got infinity. Here I am adding up an infinite number of terms and getting 2. The harmonic series is divergent. This one is convergent.
The harmonic series has its charms, and it stands at the center of the topic this book addresses—the Riemann Hypothesis. Generally speaking, however, mathematicians are more interested in convergent series than divergent ones.
V. Suppose that instead of moving one inch to the right, then a half-inch to the right, then a quarter-inch to the right, and so on, I decided to alternate directions: an inch to the right, a half-inch to the left, a quarter-inch to the right, an eighth-inch to the left.… After seven moves I’d be at the point shown in Figure 1-10.
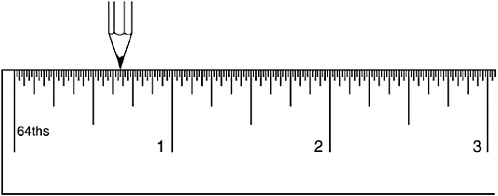
FIGURE 1-10
Since from the mathematical point of view a move to the left is just a negative move to the right, this is equivalent to
which is 
. In fact, it’s rather easy to show—I’ll prove it in a later chapter—that if you keep on adding and subtracting to infinity you get
Expression 1-2
VI. Now, suppose that instead of starting out with a ruler marked in halves, quarters, eighths, sixteenths, and so on, I have a ruler marked in thirds, ninths, twenty-sevenths, eighty-firsts, and so on. In other words, instead of halves, halves of halves, halves of halves of halves … I have thirds, thirds of thirds, thirds of thirds of thirds, and so on. And suppose I do an exercise similar to the first one, move the pencil along one inch, then a third of an inch, then a ninth, then a twenty-seventh (see Figure 1-11).
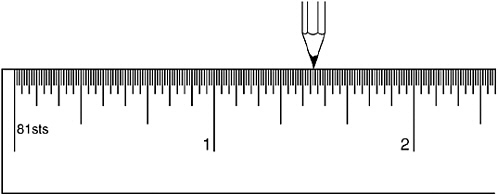
FIGURE 1-11
I don’t think it’s too hard to see that if you continue forever, you end up moving right a total 
inches as shown in Expression 1-3. That is,
Expression 1-3
And of course, I can do the alternating movement with this new ruler, too: right one inch, left a third, right a ninth, left a twenty-seventh, and so on (see Figure 1-12).
FIGURE 1-12
The math of Expression 1-4 is not so visually obvious, but it’s a fact that
Expression 1-4
So here we have four convergent series, the first (Expression 1-1) creeps closer and closer to 2 from the left, the second (Expression 1-2) closes in on 
from left and right alternately, the third (Expression 1-3) creeps closer and closer to 
from the left, the fourth (Expression 1-4) closes in on 
from left and right alternately. Before that, I showed one divergent series, the harmonic series.
VII. When reading math, it is important to know where in math you are—what region of this vast subject you are exploring. The particular zone these infinite series dwell in is what mathematicians call analysis. Analysis used, in fact, to be thought of as the study of the infinite, that is, the infinitely large, and of the infinitesimal, the infinitely small. When Leonhard Euler—of whom I shall write much more later—published the first great textbook of analysis in 1748, he called it Introductio in analysin infinitorum: “Introduction to the Analysis of the Infinite.”
The notions of the infinite and the infinitesimal created serious problems in math during the early nineteenth century, though, and eventually they were swept away altogether in a great reform. Modern analysis does not admit these concepts. They linger on in the vocabulary of mathematics, and I shall make free use of the word “infinity” in this book. This usage, however, is only a convenient and imaginative shorthand for more rigorous concepts. Every mathematical statement that contains the word “infinity” can be reformulated without that word.
When I say that the harmonic series adds up to infinity, what I really mean is that given any number S, no matter how large, the sum of the harmonic series eventually exceeds S. See?—No “infinity.” The
whole of analysis was rewritten in this kind of language in the middle third of the nineteenth century. Any statement that can’t be so rewritten is not allowed in modern mathematics. Nonmathematical people sometimes ask me, “You know math, huh? Tell me something I’ve always wondered, What is infinity divided by infinity?” I can only reply, “The words you just uttered do not make sense. That was not a mathematical sentence. You spoke of ‘infinity’ as if it were a number. It’s not. You may as well ask, ‘What is truth divided by beauty?’ I have no clue. I only know how to divide numbers. ‘Infinity,’ ‘truth,’ ‘beauty’—those are not numbers.”
What is a modern definition of analysis, then? I think the study of limits will do for my purposes here. The concept of a limit is at the heart of analysis. All of calculus, for example, which forms the largest part of analysis, rests on the idea of a limit.
Consider the following sequence of numbers: 
Each fraction is built from the one before by a simple rule: add top and bottom to get new bottom, add top and twice bottom to get new top. That sequence converges to the square root of 2. If you square 
, for example, you get 
, which is 2.000000176838287…. We say that the limit of the sequence is 
.
Here is another case: 
To get the N-th member of that sequence: if N is even, multiply the previous member by 
, if N is odd, multiply the previous member by 
. That converges to π . The last fraction shown is 2.972154… (this sequence converges very slowly). Here is yet another: 
If you work them out, these come to 
a sequence that converges to a number close to 2.718281828459. This is an exceedingly important number—I shall use it later.
Notice that all of these are sequences, just strings of numbers separated by commas. They are not series, where the numbers are actually added up. From the point of view of analysis, however, a series is just a sequence in thin disguise. The statement “The series 
converges to 2” is mathematically equivalent to: “The sequence 
converges to 2.” The fourth term of the sequence is the sum of the first four terms of the series, and so on. (The term of art for this kind of sequence is the sequence of partial sums.) Similarly, of course, the statement, “The harmonic series diverges” is equivalent to: “The sequence 
diverges,” where the N-th term of the sequence is the previous term plus 
.
This is analysis, the study of limits, of how a sequence of numbers can get closer and closer to a limiting number without ever quite reaching it. If I say the sequence goes on forever, I mean that no matter how many terms you write down, I can always write another. If I say it has the limit a, I mean that no matter how tiny a number x you pick, from some point on, every number in the sequence differs from a by less than x. If you choose to say: “The sequence is infinite,” or: “The limit of the N-th term, when N goes to infinity, is a,” you are free to do so, as long as you understand that these are just loose and convenient ways of speaking.
VIII. The traditional division of mathematics into subdisciplines is as follows.
-
Arithmetic—The study of whole numbers and fractions. Sample theorem: If you subtract an odd number from an even number you get an odd number.
-
Geometry—The study of figures in space—points, lines, curves, and three-dimensional objects. Sample theorem: The angles of a triangle on a flat surface add up to 180 degrees.
-
Algebra—The use of abstract symbols to represent mathematical objects (numbers, lines, matrices, transformations), and the study of the rules for combining those symbols. Sample
-
theorem: For any two numbers x and y, (x + y) × (x – y) = x2 – y2.
-
Analysis—The study of limits. Sample theorem: The harmonic series is divergent (that is, it increases without limit).
Modern mathematics contains much more than that, of course. It includes set theory, for example, created by Georg Cantor in 1874, and “foundations,” which another George, the Englishman George Boole, split off from classical logic in 1854, and in which the logical underpinnings of all mathematical ideas are studied. The traditional categories have also been enlarged to include big new topics—geometry to include topology, algebra to take in game theory, and so on. Even before the early nineteenth century there was considerable seepage from one area into another. Trigonometry, for example, (the word was first used in 1595) contains elements of both geometry and algebra. Descartes had in fact arithmetized and algebraized a large part of geometry in the seventeenth century, though pure-geometric demonstrations in the style of Euclid were still popular—and still are— for their clarity, elegance, and ingenuity.
The fourfold division is still a good rough guide to finding your way around mathematics, though. It is a good guide, too, for understanding one of the greatest achievements of nineteenth-century math, what I shall later call “the great fusion”—the yoking of arithmetic to analysis to create an entirely new field of study, analytic number theory. Permit me to introduce the man who, with one single published paper of eight and a half pages, got analytic number theory off the ground and flying.
