Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (2003)

I. So far I have presented the deep background to the Riemann Hypothesis—to the Prime Number Theorem (PNT) and to Riemann’s 1859 paper on that topic, in which the Hypothesis was first stated. In this chapter I shall describe the immediate background to that paper. This is really two stories intertwined: the story of Bernhard Riemann and the story of Göttingen University in the 1850s, with brief side trips to Russia and New Jersey for some local color.

You should keep in mind a broad general picture of European intellectual life in the 1830s, 1840s, and 1850s. It was, of course, a time of great change. The upheavals of the Napoleonic wars had let loose new forces of nationalism and reform. The Industrial Revolution was on the march. The shifts in thought and feeling we customarily collect under the heading “the Romantic Movement” had seeped down to the general population everywhere. The 1830s, when spirits had revived after the exhaustion of the long wars, were an unsettled time, marked by the July revolution in France, a nationalist uprising in Poland (at that time part of the Russian empire³⁹), agitation among

the Germans for national unity, and the great Reform Bills in Britain. Alexis de Tocqueville visited the United States and wrote a penetrating analysis of that curious new experiment in popular government. In the following decade darker forces stirred, culminating in 1848, “the year of revolutions,” whose disturbances, as we saw in Chapter 2, penetrated for a moment even the deep reserve of Bernhard Riemann.

Göttingen was for all this period a provincial backwater illuminated mainly by the presence of Gauss. The university’s one moment of political prominence occurred in 1837 with the dismissal of the “Göttingen Seven” that I already mentioned, the main effect of which was to lower the prestige of the university. Paris remained the great center of mathematical research, with Berlin rising fast. In Paris Cauchy and Fourier had overhauled analysis, laying the foundations of the modern treatment of limits, continuity, and the calculus. In Berlin new advances were being made by Dirichlet in arithmetic, by Jacobi in algebra, by Steiner in geometry, and by Eisenstein in analysis. Anyone who wanted to do serious mathematics in the 1840s needed to be in Paris or Berlin. That is why young Bernhard Riemann, 20 years old in the spring of 1847, disappointed with the standard of instruction at Göttingen and very keen indeed to do serious mathematics, went to Berlin. He studied there for two years, during which the greatest influence on him was Lejeune Dirichlet, the man who had picked up the Golden Key in 1837. Dirichlet took a personal liking to the shy, poverty-stricken young Riemann, an attitude which Riemann, in the words of Heinrich Weber, “reciprocated with respectful gratitude.”

Returning to Göttingen after the Easter break in 1849, Riemann embarked upon his doctorate course, under the supervision of Gauss himself. Plainly, his hope was to become a lecturer at the university. That was a long road to travel, though. To lecture at Göttingen required not only a doctorate, but also a further qualification, the “habilitation,” a sort of second doctorate, with a thesis to be prepared and a trial lecture to be given. The whole thing, doctorate and habili-

tation, took Riemann more than five years—from age 22½ to nearly age 28—during which he had no income at all.

Right away, Riemann enrolled for some courses in physics and philosophy along with math. These were required subjects for those wishing to teach in the gymnasium high-school system, pretty much Riemann’s only career choice if he could not get a lecturing position. He might have been hedging his bets by taking these courses. He had, however, a deep interest in both subjects, so it is probable that pure personal inclination was at least as much of a factor in his enrolling for them. Standards at Göttingen had improved, too. The physicist Wilhelm Weber, one of the Göttingen Seven cashiered in 1837, had returned to the university to teach, the political climate having thawed considerably. An old friend and colleague of Gauss’s—the two of them had together invented the electric telegraph—Weber taught a course in experimental physics, which Riemann attended.⁴⁰

II. Those five years of unpaid research work must have been hard ones for Bernhard Riemann. He was far from home; it was 120 miles from Göttingen to Quickborn, a two-day journey in great discomfort, and expensive. He did, though, have some company. In 1850 Richard Dedekind arrived at the university. Dedekind was 19, five years younger than Riemann, and was also aiming for a doctorate. It is plain from Dedekind’s biographical note on Riemann in the Collected Works that he felt affection and sympathy for his older colleague, and great admiration for his mathematical abilities; it is more difficult to judge Riemann’s feelings in the matter.

The two men got their doctorates within a few months of each other, Riemann in December 1851, Dedekind the following year. Both were examined by Gauss, now in his mid-70s but keenly alert to exceptional mathematical talent. On the thesis submitted by young Dedekind, still not mathematically mature, Gauss’s report is little better than boilerplate approval. On Riemann’s, he gushed—and Gauss

was a man who rarely gushed. “A substantial and valuable work, which does not merely meet the standards required for a doctoral dissertation, but far exceeds them.”

Gauss was not mistaken. (About mathematics, I doubt he ever was.) Riemann’s doctoral dissertation is a key work in the history of complex function theory. I shall attempt an explanation of complex function theory in Chapter 13. For the time being, suffice it to say that it is a very deep, powerful, and beautiful branch of analysis. To this day, almost the first things you learn in a course on complex function theory are the Cauchy-Riemann equations for a function to be well behaved and worthy of further investigation. These equations first appear in their modern form in Riemann’s doctoral dissertation. The paper also contains the first sketches of the theory of Riemann surfaces, a fusion of function theory with topology—the latter topic so new at the time there was really no coherent body of knowledge about it, only some scattered results going back to Euler’s time.⁴¹ Riemann’s doctoral thesis is, in short, a masterpiece.

Both Riemann and Dedekind then embarked on the second leg of the academic marathon to which they had committed themselves, the habilitation thesis and trial lecture required for a teaching position at the university.

III. Let us leave Bernhard Riemann for a while, toiling away at that habilitation thesis in his room at Göttingen, and step a year or two back in time, and a thousand miles away in space, to St. Petersburg. Considerable water has flowed under the bridges of that city since last we were there, watching Leonhard Euler living contentedly and working productively, even though old and blind, under the rule of Catherine the Great. Euler died in 1783, the Empress herself in 1796. Catherine was succeeded by her eccentric and irresponsible son Paul. Four and a half years of Paul proved enough for the nobility, who staged a coup, garroted Paul, and replaced him with his son Alexander.

The nation was then soon absorbed in the conflict with Napoleon, and her French-speaking aristocracy in the glittering social scenes drawn by Tolstoy in War and Peace. After a postwar spell of managerial despotism under Alexander, and in spite of the failed revolt of the liberalizing faction known as Decembrists, the throne passed in 1825 to the more old-fashioned absolutism of Nicholas I.

However, the reassertion, and re-reassertion, of the absolutist principle had not prevented great social changes, most memorably the first great flowering of modern Russian literature under Pushkin, Lermontov, and Gogol.⁴² The university at St. Petersburg, now a separate institution from the Academy, had grown and flourished, and new universities had been established in Moscow, Kharkov, and Kazan. In Kazan, the university boasted the presence of the great mathematician Nikolai Lobachevsky, who served as Rector until his dismissal in 1846. Lobachevsky was the inventor of non-Euclidean geometry, of which I shall have more to say shortly.⁴³

And now, in 1849–1850, 25 years into the reign of Nicholas I, intellectual life in Russia was enduring another spell of repression, as Nicholas reacted to the 1848 revolutions in Europe. University enrolments were slashed and Russians studying abroad were ordered home. This was the environment in which a young lecturer at the university of St. Petersburg produced two remarkable papers on the PNT.

The first thing to be said about Pafnuty Lvovich Chebyshev is that his last name is a data-retrieval nightmare. Researching for this book, I turned up 32 different transcriptions of the name: Cebysev, Cebyshev, Chebichev, Chebycheff, Chebychev, etc., etc.

And if that unusual first name, Pafnuty, caught your eye, you are not alone. It caught the eye of mathematician Philip J. Davis around 1971. Davis embarked on a quest to find the origins of “Pafnuty,” and wrote an extremely funny book about his researches, The Thread (1983). In very brief, the name “Pafnuty” is Coptic in origin (Papnute = “the man of God”), entered Europe via Egyptian Christianity, and was the name of a minor Church Father in the fourth century. Present at the Synod of Nicea, Bishop Paphnutius (as he is

usually spelled) argued against priestly celibacy. A later Pafnuty noted by Davis en passant was St. Pafnuty of Borovsk, the son of a Tartar noble, who entered a monastery at age 20 and stayed there until he died, aged 94, in 1478. Says the hagiographer of this Pafnuty: “He was a virgin and an ascetic, and, because of this, a great wonderworker and seer.” (In the middle of writing this chapter I got an e-mail from a reader of my web column asking me to suggest a name for her new dog. There is now a Pafnuty chasing squirrels somewhere in the Midwest.)

Our own Pafnuty was something of a wonder-worker himself. To him belongs the honor of having accomplished the only real advances toward a proof of the PNT in between Dirichlet’s picking up the Golden Key in 1837 and Riemann’s turning it in 1859. The curious thing is that his most original work did not flow into the mainstream of researches on the PNT, but started a lesser branch of the stream, which went underground, to emerge only 100 years later.

Chebyshev actually wrote two papers on the PNT. The first, dated 1849, is titled “On the Function that Determines the Totality of Prime Numbers Less Than a Given Limit”; notice the similarity to the title of Riemann’s paper of 10 years later. In this paper Chebyshev picked up Euler’s Golden Key, fiddled with it a little in much the way Dirichlet had 12 years before, and produced the following interesting result.

Chebyshev’s First Result

If 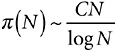for some fixed number C, then C must be equal to 1.

The problem, of course, was with that “if.” Chebyshev could not get past it, and neither, for half a century, could anyone else.

Chebyshev’s second paper, dated 1850, is much more curious. Instead of using the Golden Key, it began from a formula proved by

the Scottish mathematician James Stirling in 1730 to get approximate values of the factorial function for large numbers. (The factorial of N is 1 × 2 × 3 × 4 × … × N. The factorial of 5, for example, is 120:1 × 2 × 3 × 4 × 5 = 120. The usual symbol for the factorial of N is “N !” Stirling’s formula says that for large values of N, the factorial of N is about .) Chebyshev converted this into a different formula involving a step function—that is, a function that has the same value across a range of arguments, then jumps to another value.

With just these tools, and some very elementary calculus, Chebyshev got two important results. The first was a proof of “Bertrand’s postulate,” suggested in 1845 by the French mathematician Joseph Bertrand. The postulate states that between any number and its double (for example, between 42 and 84) there is always a prime to be found. The second was the one shown here.

Chebyshev’s Second Result

π (N) cannot differ from 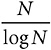by more than about ten percent up or down.

This second paper was important in two ways. First, its use of a step function might have inspired Riemann’s use of a similar function in his 1859 paper, which I shall show in detail later. It is certain that Riemann knew of Chebyshev’s work; the Russian mathematician’s name appears in Riemann’s notes (spelled “Tschebyschev”).

It is Chebyshev’s line of approach in that second paper that is more noteworthy, though. He got his results without using any complex function theory. Mathematicians have a shorthand way of expressing this fact. They say that Chebyshev’s methods were “elementary.” Riemann, in his 1859 paper, did not use elementary methods. He brought the full power of complex function theory to bear on the issue he was investigating. The results he got were so striking that other mathematicians followed him, and the PNT was proved at last using Riemann’s non-elementary methods.

That it might be possible to prove the PNT by elementary methods remained an open issue, but by the time several decades had passed, the general opinion was that no such proof was possible. Thus, in Albert Ingham’s 1932 text The Distribution of Prime Numbers, the author says in a footnote “[A] ‘real variable’ proof of the prime number theorem, that is to say a proof not involving explicitly or implicitly the notion of an analytic function of a complex variable, has never been discovered, and we can now understand why this should be so….”

Then, to everybody’s astonishment, such a proof was discovered in 1949 by Atle Selberg, a Norwegian mathematician working at the Institute for Advanced Study in Princeton, New Jersey.⁴⁴ There was much controversy over the result, because Selberg had communicated some of his preliminary ideas to the eccentric Hungarian mathematician Paul Erdős, who used them to create a proof of his own at the same time. Two popular biographies of Erdős were produced after his death in 1996, and the curious reader can find a full account of the controversy in either. The proof is called the Erdős-Selberg proof in Hungary, and the Selberg proof elsewhere.

In addition to his research, Chebyshev was a great teacher and proselytizer for his subject. His disciples took his ideas and methods to other Russian universities, inspiring interest and raising standards everywhere. Active into his 70s, Chebyshev was also a keen inventor, who built a series of calculating machines still preserved at museums in Moscow and Paris. A lunar crater is named after him; it is at about 135°W 30°S.⁴⁵

IV. I cannot leave Chebyshev without at least a passing mention of his famous bias—famous among number theorists, I mean.

If you divide a prime number (other than 2) by 4, the remainder must be either 1 or 3. Do the primes show any preference? Yes, they do: up to p = 101, there are 12 remainder-1 primes and 13 remainder-3’s.

Up to p = 1,009, the tallies are 81 and 87. Up to p = 10,007, they are 609 and 620. Clearly, the remainder-3’s have a small but persistent edge over the remainder-1’s. This is an example of a Chebyshev bias, first remarked on by Chebyshev in a letter dated 1853. This particular bias is eventually violated at p = 26,861, when remainder-1’s snatch a momentary lead. Even that is only a one-time aberration, though: the first real zone of violation is the 11 primes from p = 616,877 to 617,011. Remainder-1’s hold the lead at only 1,939 of the first 5.8 million primes, which is as far as I checked. They don’t hold it once in the last 4,988,472 of those primes.

With divisor 3, the bias is even more dramatic. Here, the remainder (once you get past p = 3) can be either 1 or 2, and the bias is to 2. This bias is not violated until p = 608,981,813,029. Now that is a bias! This violation was tracked down in 1978, by Carter Bays and Richard Hudson. I shall have occasion to mention the Chebyshev bias again, in Chapter 14.

V. In the fall of 1852, the first year of work on his habilitation thesis, Riemann met Dirichlet again. The whole episode is rather touching, and I transcribe it here from the biography by Dedekind.

That last remark shows the demands Riemann placed on himself, his powerful sense of duty, and his determination to justify every minute of his time at Göttingen to himself, to his father (who, after all, was supporting him), and to God.

The procedure for habilitating was that Riemann should first submit a written thesis, then prepare a trial lecture to be delivered before the faculty. The thesis itself—it is titled “On the representability of a function by a trigonometric series”—is a landmark paper, giving the world the Riemann integral, now taught as a fundamental concept in higher calculus courses. The habilitation lecture, however, far surpassed the thesis.

Riemann was supposed to offer three lecture titles from which Gauss, his supervisor, would pick one to be delivered. Riemann’s three offerings were of two topics in mathematical physics and one in geometry. Gauss picked the lecture titled “On the Hypotheses that Lie at the Foundations of Geometry,” and Riemann delivered it to the assembled faculty on June 10, 1854.

This is one of the top 10 mathematical papers ever delivered anywhere, a sensational achievement. Its reading was, declares Hans Freudenthal in the Dictionary of Scientific Biography, “one of the highlights in the history of mathematics.” The ideas contained in this paper were so advanced that it was decades before they became fully

accepted, and 60 years before they found their natural physical application, as the mathematical framework for Einstein’s General Theory of Relativity. James R. Newman, in The World of Mathematics, refers to the paper as “epoch-making” and “imperishable” (but fails to include it in his huge anthology of classic mathematical texts). And the astonishing thing is that the paper contains almost no mathematical symbolism. Leafing through it, I see five equals signs, three square root signs and four Σ signs—an average of fewer than one symbol per page! There is just one real formula. The whole thing was written to be understood—or perhaps (see below) misunderstood—by the average faculty member of a middling provincial university.

Riemann’s starting point was some ideas Gauss had put forward in an 1827 paper titled “A General Investigation into Curved Surfaces.” Gauss had been employed for the previous few years in carrying out a detailed topographical survey of the Kingdom of Bavaria (during which, by the way, he invented the heliotrope, a device for making long-distance observations by reflecting flashes of sunlight from an arrangement of mirrors). Gauss’s stupendous mind had abstracted from the material he was dealing with some ideas about the properties of two-dimensional surfaces, and the way those properties might be described mathematically. Gauss’s paper is generally regarded as the starting point for the subject named “differential geometry.”

Riemann, in his habilitation lecture, took up these ideas and generalized them to spaces of any number of dimensions. More significantly, he brought in quite a new way of looking at the topic. Gauss saw it all, in his imagination, in terms of curved two-dimensional sheets embedded in ordinary three-dimensional space from which they could be viewed—the natural abstraction from his experiences as a land surveyor. Riemann shifted the point of view to one that was interior to the space under consideration.

I imagine you are familiar with the idea contained in Einstein’s General Theory of Relativity, that the three dimensions of space and one of time can be dealt with mathematically as a four-dimensional

space-time, and that this four-dimensional continuum is warped and puckered by the presence of mass and energy. From the Gaussian point of view, the geometry of this space-time would have been developed by imagining it imbedded in a five-dimensional continuum, in the way that Gauss thought of his two-dimensional surfaces as embedded in ordinary three-dimensional space. That modern physicists do not think of space-time in this way is due to Riemann. In fact, if you were to go down to your local university and sign up for a course in the General Theory of Relativity, these would be the topic headings you might cover, in order:

• The metric tensor

• The Riemann tensor

• The Ricci tensor

• The Einstein tensor

• The stress-energy tensor

• Einstein’s equation G = 8πT

You would then have mastered the essentials of the General Theory.

Though I am concerned in this book to describe Riemann’s discoveries in arithmetic and the great Hypothesis that sprang from them, these geometrical researches of his are not entirely off the topic. Riemann’s general cast of mind, and all his best mathematical work, arose from a tension between two contrary sets of ideas. On the one hand he was a great globalist, whose tendency was always to see things in the large. A function was not, for Riemann, a mere set of points; still less was it any of its pictorial representations as a graph or a table; and still less a collection of expressions involving algebraic formulas. (In one of his few recorded negative comments about anyone at all, Riemann noted that the Berlin mathematician Gotthold Eisenstein “stopped at formal computation.”) What, then, was a function? It was an object, from which none of its attributes could properly be detached. Riemann saw a function the way chess grandmasters are said to see a game, all at once, as a unified whole, a Gestalt.

Yet in tension with this was an opposing tendency, also very marked in Riemann’s work—the tendency to reduce every mathematical topic to analysis. “Riemann … always thought in analytic terms,” says Laugwitz. The writer is thinking here of the infinitesimal aspect of analysis; of limits, continuity, smoothness—of the local properties of numbers, functions, and spaces. It is, when you think about it, very odd that inquiries about the infinitesimal neighborhoods of points and numbers should give us the power to explain the large global properties of functions and spaces. This is especially apparent in General Relativity theory, where you start off by analyzing microscopic regions of space-time and end by contemplating the shape of the universe and the death throes of galaxies. That we are able to think in this extraordinary way, in both pure and applied mathematics, is mainly due to the mathematicians of the early nineteenth century, and most of all to Bernhard Riemann.

That great habilitation lecture is, in fact, as much a philosophical document as a mathematical one. In this respect the much-remarked obscurity of some of its passages might have been deliberate on Riemann’s part. (Though see Freudenthal’s remark below.) What he was speaking about at its most fundamental was the nature of space. Now, to the average complacent elderly academic of the time—the kind of person who would have been among the Göttingen faculty listening to Riemann’s lecture that June day—the nature of space was a settled matter. It had been settled 70 years earlier by Immanuel Kant in The Critique of Pure Reason. Space is a pre-existing part of our mental equipment, with which we organize our sense impressions, and it is necessarily Euclidean—that is, flat, with a straight line being the shortest distance between two points, and the angles of a triangle adding up to 180 degrees.

The non-Euclidean geometry described by Lobachevsky in the 1830s was, seen from this point of view, a philosophical heresy. Riemann’s paper was an enlargement of that heresy; and this might be why he presented his ideas at such a very general level that their connection with non-Euclidean geometry would have escaped all but

the most mathematically adept in his audience. (But not, of course, Gauss. Gauss had in fact invented non-Euclidean geometry for himself, but had not published his findings, “for fear,” as he wrote in a letter to a friend, “of the hue and cry of the blockheads.” Nineteenth-century Germans took their philosophy seriously.)

Hans Freudenthal, in the Dictionary of Scientific Biography note mentioned above, has the following to say about Riemann’s philosophical abilities.

I am not qualified to judge whether this is true. I can, however, give wholehearted assent to another remark of Freudenthal’s: “Riemann’s style, influenced by philosophical reading, exhibits the worst aspects of German syntax; it must be a mystery to anyone who has not mastered German.” I confess that, though I possess a copy of Riemann’s collected works in the original German—it is a single volume of 690 pages—and have done my best with his actual words, where he departs from straightforward mathematical exposition— as, for example, in the habilitation lecture—I have approached his tremendous thoughts mainly through translations and secondary sources.⁴⁶

VI. Dedekind habilitated shortly after Riemann, and both mathematicians began lecturing in the fall-winter term of 1854, Riemann now 28, Dedekind 23. For the first time in his life, Riemann had a salary. It can’t have been much of a salary, though. Ordinary lecturers were paid by the students who attended their lectures (technically by the university, which forwarded the students’ fees to the lecturers).

There were few students of mathematics at Göttingen at this time— Riemann’s first lecture drew eight—and lectures were frequently canceled because nobody enrolled for them. Riemann and Dedekind seem to have attended each other’s lectures, though whether they paid each other the requisite fees, I have not been able to discover.

There was further the problem that Riemann seems to have been a poor lecturer. Dedekind is frank about this.

Dedekind, ever sympathetic to his subject, goes on to claim that Riemann’s lecturing style improved over the years. This might be true; but surviving letters by Riemann’s students suggest that as late as 1861 “His thoughts frequently failed him and he was unable to explain the simplest things.” Riemann’s own take on the matter is, as usual, rather touching. Writing to his father after his first lecture, which was on October 5, 1854, he says “I hope that in half a year I shall feel easier about my lectures, and the thought of them will not spoil my stay in Quickborn and my being together with you, as last time.” This was a desperately shy man.

VII. The great event of that fall-winter term was the death of Gauss on February 23, 1855, at the age of 77. Though not in good health

toward the end, he died quickly, of a heart attack, while sitting in his favorite chair in his beloved observatory.⁴⁷

Gauss’s professorship was immediately offered to Dirichlet, who accepted, arriving in Göttingen a few weeks later. Recalling how generously Dirichlet had treated him in Berlin, and their bonding during the older man’s visit to Göttingen in 1852, Riemann must have been pleased. Gauss’s brain, meanwhile, was pickled and stored in the university’s physiology department, where it remains to this day.

Dirichlet was pleased, too; he had been seriously overworked in Berlin. Whether his wife was pleased is not so certain. Accustomed to the high society of Berlin, Rebecca Dirichlet, née Mendelssohn, must have thought Göttingen very dull and provincial. She did her best with the place, organizing balls—Dedekind mentions one attended by 60 or 70 people—and musical soirées in the Berlin style. Dedekind himself thrived in this environment, being sociable and musical. Riemann was, of course, a different case, and if his friend ever persuaded him to attend one of these functions, poor Riemann must have endured it in an agony of self-consciousness.

He experienced much deeper agony in October of that year, 1855, when his father died, followed very shortly by his younger sister Clara. Now the cherished link with Quickborn was broken. Riemann’s brother had a position as postal clerk in Bremen and Riemann’s three remaining sisters, having no other means of support, nor even accommodation (since the vicarage at Quickborn was taken over by the new pastor), went to live with him there.

Poor Riemann must have been devastated. He threw himself into work, and in 1857 produced the landmark paper on function theory that I mentioned in Chapter 1, the paper that made his name known. The effort, however, combined with grief, precipitated a nervous breakdown. Dedekind’s family had a summer home in the Harz mountains a few miles west of Göttingen. He persuaded Riemann to spend a few weeks there and joined him briefly, going for walks with him.

After Riemann’s return to Göttingen in November, he was appointed Assistant Professor at the university, with a modest salary of 300 thalers a year. But now calamities came thick and fast. His brother Wilhelm died in Bremen that same month, then, early the following year, his sister Marie. The family that Riemann adored, and that was the entire focus of his emotional life, was disappearing before his eyes. He brought the two surviving sisters to stay with him at Göttingen.

In the summer of 1858 Dirichlet suffered a heart attack while lecturing in Switzerland and was brought back to Göttingen only with much difficulty. While he was lying gravely ill, his wife died suddenly of a stroke. Dirichlet himself followed her the next May. (His brain joined Gauss’s in the department of physiology.) Gauss’s chair was now empty.

VIII. From the death of Gauss to the death of Dirichlet was four years, two months, and twelve days. In that span, Riemann lost not only the two colleagues he had esteemed above all other mathematicians, but also his father, his brother, two of his sisters, and the vicarage at Quickborn—the one place that had been a home and refuge to him since his infancy.

While his emotional life had been visited by these traumas, Riemann’s star in the world of mathematics had been rising. By the end of the 1850s, the brilliance and originality of his work were known, at some level, to mathematicians all over Europe. The painfully shy young student who had shown up to begin his doctoral studies 10 years earlier was now a mathematician of note, and Göttingen, which had entered the 1850s as the home of Gauss, was beginning to be spoken of as the home of Gauss, Dirichlet, and Riemann. (Though not of Dedekind, whose best work was still in front of him. Dedekind had, in fact, left Göttingen to take up a post in Zürich in the fall of 1858.)

It was, therefore, not very surprising that the authorities selected Riemann as the second successor of Gauss. On July 30, 1859, he was given a full professorship, an assured livelihood, and—probably as an acknowledgment of his need to support his two surviving sisters— Gauss’s apartments at the observatory. Other honors soon followed. The first came on August 11, when he was appointed a corresponding member of the Berlin Academy. Riemann returned to Berlin a little more than 10 years after he had left, but now he came with a modest set of laurels on his brow, to be received with honor by the great names of German mathematics: Kummer, Kronecker, Weierstrass, Borchardt.

To crown his triumph, Riemann gave the Academy his paper on “the number of primes less than a given quantity.” In the paper’s first sentence he acknowledged the two men, both now dead, with whose aid—though given much more willingly in Dirichlet’s case than in Gauss’s—he had scaled the heights. In the second sentence he showed the Golden Key. In the third he named the zeta function. Here, in fact, are the first three sentences of Riemann’s 1859 paper.

The Riemann Hypothesis, which appears on the fourth page of that paper, asserts a certain fact about the zeta function. To advance in our understanding of the Hypothesis, we must now go deeper into the zeta function.