Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (2003)

I. There should actually be a lot of algebra in this book, much more than I have been able to present. My focus has been on Bernhard Riemann and his work on prime numbers and the zeta function. That work was in number theory and analysis, and so my narrative has been dominated by those topics. However, modern math is, as I have already noted, very algebraic. This chapter fills in the algebraic background you need to understand two important approaches to the Riemann Hypothesis.

Like Chapters 7 and 15, this is a twofer chapter. Sections II and III give the basics of field theory; the remainder of the chapter discusses operator theory. Field theory is important because it has allowed something very much like the Riemann Hypothesis to actually be proved. Many researchers believe that field theory offers the most promising line of attack on the original, classical Riemann Hypothesis.⁹⁹ Operator theory became important following the remarkable and rather romantic developments I shall describe in the next chapter. First, though, field theory.

II. “Field” has a very particular meaning to mathematicians. A set of elements forms a field if the elements can be added, subtracted, multiplied, and divided, according to the ordinary rules of arithmetic—for example, the rule that a × (b + c) = ab + ac. The results of all these operations must stay within the field.

For example, is not a field. If you try to subtract 12 from 7, you get a result that is not in . Similarly with . If you divide 12 by 7, the answer is not in . These are not fields.

However, , , and are all fields. If you add, subtract, multiply, or divide two rational numbers, you get another rational number. Likewise with real and complex numbers. These are three examples of fields. Each has an infinite number of elements, of course.

Other infinite fields are easy to construct. Consider the family of all numbers with the form , where a and b are rational numbers. Either b is zero, or it isn’t. If b is not zero, since is not a rational number, is not a rational number either. This family therefore includes all the rationals (b zero) as well as a host of very particular irrationals. It is a field. Adding to gives , subtracting gives , multiplying gives and dividing, using a trick similar to the one for complex numbers, gives . Since a and b can be any rational numbers at all, the field has infinitely many members.

Fields do not have to be infinite. Here is the simplest of all fields, with only two elements, 0 and 1. The rules for addition are: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 0. The rules for subtraction are: 0 – 0 = 0, 0 – 1 = 1, 1 – 0 = 1, 1 – 1 = 0. (Notice that these results are the same as for addition. In this field, any minus sign can be freely replaced by a plus sign!) The rules for multiplication are: 0 × 0 = 0, 0 × 1 = 0, 1 × 0 = 0, 1 × 1 = 1. The rules for division are: 0 ÷ 1 = 0, 1 ÷ 1 = 1, and division by zero is not allowed. (Division by zero is never allowed.) That is a perfectly sound field, and by no means trivial; I shall make good use of it in a moment. Mathematicians call it “F₂.”

You can, in fact, construct a finite field for any prime number p, and even for any power of any prime number. If p is a prime number, there is a finite field with p members, one with p² members, one with p³ members, and so on. Furthermore, these are all the possible finite fields. You can list them: F₂, F₄, F₈, …, F₃, F₉, F₂₇, …, F₅, F₂₅, F₁₂₅, …, …; and when you have done so, you have listed all possibilities for finite fields.

It is a mistake to think, as beginners often do, that finite fields are just a restatement of the clock arithmetic I described in Chapter 6.viii. This is true only for fields with a prime number of members. For other finite fields, the arithmetic is more subtle. Figure 17-1, for example, shows the clock arithmetic—addition and multiplication— for a clock with four hours marked (i.e., 0, 1, 2, and 3).

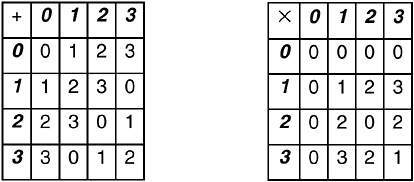
FIGURE 17-1 Addition and multiplication on a 4-hour clock. (That is, carrying out addition and multiplication in the usual way, then taking remainders after division by 4.)

This system of numbers and rules is interesting and useful, but it is not a field, because you can’t divide 1 or 3 by 2. (If you could divide 1 by 2, then the equation 1 = 2 × x would have a solution. It doesn’t.) Mathematicians call it a ring—not unreasonably, since we are talking about clocks. In a ring, you can add, subtract, and multiply, but not necessarily divide.

The particular ring shown in Figure 17-1 has the official symbol /4. I confess I have never liked this style of symbolism though, so I

am going to exercise author’s privilege and create a symbol of my own for it: ₄. Plainly, you can create such a ring for any natural number N. In my symbols, that ring would be called _N.

You can’t create a field F_N for every number N, only for primes and prime powers. For a pure prime p, F_p looks just like _p— same addition table, same multiplication table. For a power of a prime, however, things get trickier. Figure 17-2 shows addition and multiplication (from which, of course, you can deduce subtraction and division) in F₄. Notice that F₄ is different from ₄.

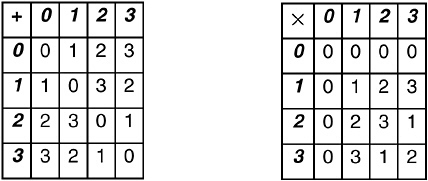
FIGURE 17-2 Addition and multiplication in the finite field F₄.

Every field, finite or infinite, has an important property called the characteristic. The characteristic of a field tells you how many times you have to add 1 to itself to get zero. If 1 + 1 + 1 + 1 + … (N times) = 0, then the characteristic is N. Obviously the characteristic of F₂ is 2. Less obviously, but you will see it if you check the addition table in Figure 17-2, the characteristic of F₄ is also 2. Fields like , , and , in which no amount of adding 1 to itself will ever produce zero, are said to have characteristic zero. (You might think that characteristic infinity would be more logical, and you might be right, but there are good reasons for choosing zero instead.) It can be proved that every field has characteristic either zero or a prime number.

Since this is algebra, the elements of a field need not be numbers. Algebra can deal with any kind of mathematical object. Consider all polynomials of any degree, that is, all expressions like axⁿ + bx^n–1 + cx^n–2 + …, where a, b, c, and so on are integers. Now form the set of all

rational functions—that is, any function that is the ratio of two polynomials. That is a field. Here is an example of an addition sum in the field.

(This is the kind of thing that high school algebra classes used to be devoted to.)

The coefficients of the polynomials in that field don’t have to be integers. You can have some fun, in fact, by making them members of a finite field, like the F₂ I defined above. Here is an example of the kind of addition sum you would then get

(Remember if you check this out, that in the F₂ field, 1 + 1 = 0; therefore, x + x = 0, x² + x² = 0, and so on.) That field would be called “the field of rational functions over F₂.” It has, of course, infinitely many members; only the coefficients are restricted to a finite field. Thus, you can use a finite field to build up an infinite field. Notice also that since 1 + 1 = 0, this field has characteristic 2. Thus an infinite field can have a finite characteristic.

It is not very helpful to ask what x represents in these last two examples. It is a symbol, for the manipulation of which we have watertight rules. From the algebraic point of view, that is the main thing. As a matter of fact, the answer to the question is almost certainly “x represents a number.” However, the algebraist is much more interested in what kind of number—to what families, what groups, what fields the number belongs, and what rules of manipulation it obeys. To the analyst, my number is not very interesting. “It is just a real number,” the analyst will say—“all right, an algebraic number” (Chapter 11.ii), if pressed. To the algebraist, though, it is exquisitely interesting, because it represents a field. For the most part, analysts

and algebraists are not really discussing different things; they are just interested in different aspects of those things.¹⁰⁰

III. That glimpse of the scope, power, and beauty of algebraic field theory is all I have space for here, though I shall revisit these topics briefly, from a different angle, in Chapter 20.v. I have given some coverage of these ideas because in 1921 the Austrian mathematician Emil Artin, in his Ph.D. thesis at the University of Leipzig, used field theory to open up a new approach to the Riemann Hypothesis. The math here is deep, and I can give only a sketch.

I mentioned in the previous section that there is a finite field for any prime power p^N. I also showed how a finite field can be used as a basis for building other fields, including even infinite ones. It turns out that if you start from a finite field, there is a way to construct one of these “extension” fields in such a way that a zeta function can be associated with it. By “a zeta function,” I mean a function of a complex argument, defined over the field of complex numbers, that bears an uncanny resemblance, in its broad properties, to Riemann’s zeta function. For example, these analogues to the Riemann zeta function come with their own Golden Keys, their own Euler products (see Note 36), and their own Riemann Hypotheses.

In 1933 Helmut Hasse, working at the University of Marburg in Germany, was actually able to prove a result analogous to the Riemann Hypothesis for a certain category of those base fields. In 1942 André Weil¹⁰¹ extended this proof to a much wider class of objects and conjectured that similar results would apply to yet wider classes— these were the famous three “Weil Conjectures.” In 1973 the Belgian mathematician Pierre Deligne, in a sensational achievement that won him a Fields Medal, proved the Weil Conjectures, essentially completing the program initiated by Artin.

Whether the techniques developed to prove these analogues of the Riemann Hypothesis for these very abstruse fields can be used to

solve the classical Hypothesis is not known. A great many people think they can, and this remains a very active area of Riemann Hypothesis studies.

Are these researchers on to something? It is not clear—not, at any rate, to me. For the crux of the matter, go back to the second paragraph in this section, where I said that one of these analogue zeta functions is associated with a certain kind of field. For the classical zeta function, the one to which the original Riemann Hypothesis applies—the one this book is mainly about—the equivalent associated field is , the field of ordinary rational numbers. As investigations have proceeded through these past few decades, it has become apparent that this elementary rational number field is in some sense deeper and more intractable than the subtle, artificial fields to which the results of Artin, Weil, and Deligne apply. On the other side of the argument, though, the techniques developed for the manipulation of those artificial fields have considerable power—Andrew Wiles used them to prove Fermat’s Last Theorem!

IV. The physical thread of Riemann Hypothesis studies, whose genesis I shall describe in Section VI, and which has opened up wide new territories for exploration, depends on some understanding of a different algebraic topic, operator theory. I have, therefore, given over this section and the next to an account of operators, approaching them by way of the related theory of matrices.

Matrices are all over the place in modern math and physics, and the ability to manipulate them is a fundamental modern mathematical skill. Since my space is limited, I am going to simplify the whole business, giving just the bare essentials. In particular, I am going to ignore the entire issue of singular matrices, as if no such things existed. This is perhaps the most brazen act of simplification in the book, and I apologize to mathematically fastidious readers.

A matrix is a square array of numbers, like this, 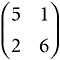. I am using just whole numbers for simplicity. The numbers in a matrix can be rational, real, or even complex. That particular matrix is a 2 × 2. A matrix can be any size, though: 3 × 3, 4 × 4, 120 × 120, and so on. It can even be infinite in size, though the rules change slightly for infinite matrices. An important part of every matrix is the lead diagonal, the one that runs from top left to bottom right. In my example, the lead diagonal has elements 5 and 6.

Given two matrices of the same size, you can add, subtract, multiply, and divide them. The rules for doing this are not straightforward; for example, if A and B are matrices of the same size, it is not generally true that A × B = B × A. You can find the rules for manipulating matrices in any decent algebra textbook, and I don’t need to go into them here. Suffice it to say that they exist and that there is an arithmetic of matrices, rather like the arithmetic of ordinary numbers, only trickier.

The important thing about matrices for us here is this. From any N × N matrix you can extract a polynomial of the N-th degree—that is, a function made up of various powers of x, up to the N-th power. I’m afraid I can’t explain just how you find the characteristic polynomial of a given matrix. You must trust me, it’s there, and there is a way to find it. This polynomial is called the characteristic polynomial of the matrix.

The characteristic polynomial of my example 2 × 2 matrix is x² – 11x + 28. For what values of x is this polynomial equal to zero? This is the same as asking, what are the solutions of the quadratic equation x² – 11x + 28 = 0? By the well-known formula (or, as my own schoolmaster used to say optimistically, “by inspection”) the solutions are 4 and 7. And sure enough, if you substitute 4 for x, the polynomial has value 16 – 44 + 28, which is indeed zero. Same with 7:49 – 77 + 28 is zero, too.

All this illustrates a general truth. Any N × N matrix has a characteristic polynomial of degree N, and that polynomial has N zeros.¹⁰²

The zeros of a matrix’s characteristic polynomial are tremendously important. They are called the eigenvalues of the matrix. Notice another thing. If you add up the numbers in the lead diagonal of my sample 2 × 2 matrix, you get 11 (because 5 + 6 = 11). That is also the sum of the eigenvalues (7 + 4 = 11); and it is the negative of the first number that appears in the characteristic polynomial (the negative of –11 is 11). This is a very important number, called the trace of the matrix.

Characteristic polynomial; eigenvalues; trace—what’s this all about? You see, the importance of matrices is not in themselves, but in what they represent. Matrix arithmetic, once you get the hang of it, is a merely mechanical skill, like ordinary arithmetic. But just as ordinary numbers can be used to represent much deeper, more fundamental things, so can matrices. It takes me 12 minutes to walk from my house to Huntington village; the distance is about 0.8 miles. If, starting tomorrow, the United States were to switch to the metric system, I should have to say “about 1.3 kilometers” instead of “about 0.8 miles.” The distance, however, would not have changed; only the numbers used to represent it would have changed. It would still take me 12 minutes to walk it (until we switch to a metric clock).

To take another example, the calendar on my wall is a way of representing, in numbers, the motions of the sun and moon. Mainly of the sun, since we Americans have a solar calendar, whose months are out of sync with the motions of the moon. My calendar, however, was given to us by a local Chinese restaurant. If I look at it closely, I can see the months and days of the traditional Chinese lunar calendar marked, each month beginning with a new moon. The numbers are all different from the solar numbers, but they represent the same celestial events, the same passage of time, the same actual days.

Just so with matrices. The great importance of matrices is that they can be used to represent, to quantify, certain deeper and more fundamental things. What are those things? They are operators. The notion of an operator is one of the most important in twentieth-century math, and also in physics. I don’t want to go into detail about

what operators are, not until Chapter 20 at any rate. The important thing to grasp is that they are lurking underneath all this business of matrices, and it is their properties that matrices allow us to measure and study numerically.

That is why the characteristic polynomial, the eigenvalues, and the trace are such key concepts. They are properties of the underlying operator, not just of the matrix that represents it. An operator can, in fact, be represented by many matrices, all having the same eigenvalues, and so on. My sample 2 × 2 matrix represents a certain operator, the matrix 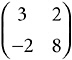represents the same operator. So does 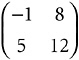, so does . All these matrices—and an infinity of others, too—have the characteristic polynomial x² – 11x + 28, the eigenvalues 4 and 7, and trace 11. That is because the underlying operator has those properties.

All of this applies to matrices of any size. Here is a 4 × 4 matrix.

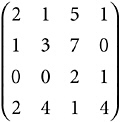
Its characteristic polynomial is x⁴ – 11x³ + 40x² – 97x + 83. (Notice that this matrix, like the other one, has trace 11. This is just coincidence; they are otherwise unrelated.) That polynomial has a full set of four zeros. To five decimal places, they are: 1.38087, 7.03608, 1.29152 – 2.62195i, and 1.29152 + 2.62195i. Those are, of course, the eigenvalues of the matrix. Two of them, as you can see, are complex numbers. (And complex conjugates of each other—which is always the case for a polynomial with real coefficients.) That is quite normal, even when, as here, all the numbers in the home matrix are real num-

bers. If you add up the four eigenvalues, you get 11; the imaginary components cancel out on addition.

V. By the time mathematicians had studied matrices for a few decades, they had classified them into different types. They had developed, so to speak, a taxonomy of matrices, in which the entire family of N × N matrices—referred to by mathematicians as “the general linear group for N,” and symbolized by “GL_N”—was organized into species and genera.

I am going to pluck just one species out of that great matrix zoo, the Hermitian matrix, named after the great French mathematician Charles Hermite, whom we met briefly in Chapter 10.v. The numbers in a Hermitian matrix are complex numbers and they have the following pattern; if the number in the m-th row of the n-th column is a + bi, then the number in the n-th row of the m-th column is a – bi. In other words, every element of the matrix is the complex conjugate (Chapter 11.v) of its reflection in the lead diagonal. An example will, I hope, make this clear. Here is a 4 × 4 Hermitian matrix.

You see how the element in the third row, first column is the complex conjugate of the one in the first row, third column? That’s a Hermitian matrix. Note that it follows from the definition that all the numbers in the lead diagonal must be real, because the definition requires each number in the diagonal to be its own complex conjugate, and only a real number can be its own complex conjugate: a + bi = a – bi if and only if b is zero.

Now, there is a famous theorem about Hermitian matrices, which says that all the eigenvalues of a Hermitian matrix are real. This is pretty surprising, when you think about it. Even if all the elements of a matrix are real, the eigenvalues can still be complex, as I showed with my first 4 × 4 matrix example. That a matrix with complex elements should nonetheless have real eigenvalues is remarkable. Well, if the matrix is Hermitian, it does. The eigenvalues of that matrix I just showed are (approximately): 4.8573, 12.9535, –16.553, and –3.2578. All real (and adding up to –2, the trace).

This theorem, by the way, implies that all the coefficients of the characteristic polynomial of a Hermitian matrix are real. This follows from the fact that the eigenvalues of any matrix are, by definition, the zeros of the matrix’s characteristic polynomial. If a polynomial has zeros a, b, c, …, then it can be factorized as (x – a)(x – b)(x – c)…. You can just multiply out all the parentheses to get back to the usual form of the polynomial. Well, if a, b, c, … are all real numbers, then multiplying out those parentheses gives you an expression with real-number coefficients. Since I have already stated the eigenvalues of the 4 × 4 Hermitian matrix above, we know that the characteristic polynomial is (x – 4.8573)(x – 12.9535)(x + 16.553)(x + 3.2578). If you multiply out all the parentheses, you get the following as the characteristic polynomial: x⁴ + 2x³ – 236x² + 286x + 3393.

VI. This was all known 100 years ago … at the time, that is, when David Hilbert was just embarking on his investigation of integral equations, in which the study of operators played a key role. Other mathematicians—some independently, some inspired by Hilbert’s work—also spent the early years of the twentieth century absorbed in the study of operators. It was in the air. The Riemann Hypothesis was not nearly so much in the air at this point; although following Hilbert’s 1900 address and the publication of Landau’s book in 1909, a lot of the best minds were beginning to think hard about it.

It is, therefore, not altogether surprising that the two things came together in two of the most brilliant and wide-ranging intellects of the time. One of those intellects was Hilbert’s, the other was George Pólya’s, and they seem to have reached the same insight independently. Their thought processes probably went something like this.

Mathematicians of the 1910s would actually have said “operator,” not “matrix.” Matrices, though they had been lying around since Arthur Cayley invented them in 1856, did not become common currency until quantum mechanics took off around 1925. Still, you can see the rough analogy here. With both the eigenvalues of a Hermitian matrix and the non-trivial zeta zeros, we have a list of unexpectedly real numbers emerging from the key property of an essentially complex object. Hence,

The Hilbert-Pólya Conjecture

The non-trivial zeros of the Riemann zeta function correspond to the eigenvalues of some Hermitian operator.

The origins of the Conjecture are rather murky. Both Hilbert and Pólya are supposed to have mentioned the possibility of some such equivalence in lectures or conversations, at some time in the years 1910–1920. However, neither, so far as I have been able to discover, committed the thought to paper for publication. So far as I know—

FIGURE 17-3 Part of George Pólya’s letter to Andrew Odlyzko.

and, says Peter Sarnak, so far as he knows—the only written evidence for the Hilbert-Pólya Conjecture having been conjectured consists of a letter Pólya wrote to Andrew Odlyzko 60 years later, part of which is shown in Figure 17-3. In it, Pólya said that he had been asked the following question by Edmund Landau: “Can you think of any physical reason why the Riemann Hypothesis might be true?” Of Hilbert’s own conjecturing, there is no material evidence at all that I am aware of.

It must be remembered, though, that Hilbert was a figure of towering stature in early twentieth-century mathematics; and also that he lived and worked in the atmosphere of German academia, where university professors were looked up to by their students and subordinates as remote and omniscient gods, to be approached only with the utmost deference. Not only was a professor not ever to be addressed as anything less elevated than “Herr Professor,” even his wife became “Frau Professor.” For the very grandest of these Olympians, indeed, even “Herr Professor” was inadequate. The most exceptional individuals were awarded the title “Geheimrat” by the German government—a rank roughly equivalent to a British knighthood. The correct form of address was then “Herr Geheimrat,” though Hilbert himself did not care for this level of formality.

Given all of this, it is not surprising that if by good fortune you got sufficiently close to one of these deities to hear him speak, you would not soon forget his words. It is also the case, to be sure, that such giants caused a certain amount of unverifiable apocrypha to be generated about them. Still, I think the balance of the evidence, circumstantial though it be, leads one to believe that Hilbert did, indeed, at some point utter the Hilbert-Pólya Conjecture, or something equivalent to it. (To simply say “the Pólya Conjecture” would be confusing, by the way, as there is another, different conjecture known by that name.)