Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (2003)

I. Well, how many primes are there less than a given quantity? I’m going to tell you very soon, but first, the five-minute refresher course on prime numbers.

Take a positive whole number—I’ll take 28 as an example. What numbers divide exactly into it? The answer is: 1, 2, 4, 7, 14, and 28. These are the factors of 28. We say: “28 has six factors.”

Now, every number has 1 as a factor; and every number has itself as a factor. These are not very interesting factors. They are, to use a word mathematicians rather like, “trivial” factors. The interesting factors are the others: 2, 4, 7, and 14. These are called the proper factors.

The number 28, therefore, has four proper factors. The number 29, however, has no proper factors. Nothing divides into 29 exactly, except, of course, 1 and 29. It is a prime number. A prime number is one with no proper factors.

Here are all the prime numbers up to 1,000.

As you can see, there are 168 of them. At this point, someone usually objects that 1 is not included in this or any other list of primes. It fits the definition, doesn’t it? Well, yes, strictly speaking, it does, and if you want to be a barrack-room lawyer about it, you can write in a “1” at the start of the list for your own satisfaction. Including 1 in the primes, however, is a major nuisance, and modern mathematicians just don’t, by common agreement. (The last mathematician of any importance who did seems to have been Henri Lebesgue, in 1899.) Even including 2 is a nuisance, actually. Countless theorems begin with, “Let p be any odd prime.…” However, 2 pays its way on balance; 1 doesn’t, so we just leave it out.

If you look closely at the list of primes, you’ll see that they thin out as you go along. Between 1 and 100 there are 25 primes; between 401 and 500, 17; and between 901 and 1,000, only 14. The number of primes in any block of 100 whole numbers seems to decline. If I continued the list to show all the primes up to a million, you would see that there are only eight primes in the last hundred-block (i.e., from 999,901 to 1,000,000). If I took it to a trillion, there would be just four in the last hundred-block. (Here they are: 999,999,999,937; 999,999,999,959; 999,999,999,961; and 999,999,999,989.)

II. The question naturally arises, Do the primes eventually thin out to nothing? If I continued the list into the trillions of trillions, and trillions of trillions of trillions of trillions, would I eventually reach a point beyond which there are no more primes, so that the last prime on my list would be the last prime, the biggest prime?

The answer to that was found by Euclid around 300 B.C.E. No, the primes never thin out to nothing. There are always more. There is no biggest prime. However big a prime you find, there is always a bigger one yet to be found. The primes go on forever. Proof: Suppose N is a prime. Form this number: (1 × 2 × 3 × … × N) + 1. This number doesn’t divide exactly by any number from 1 to N—you always get remainder 1. So either it doesn’t have any proper factors—and therefore is itself a prime bigger than N—or its smallest proper factor is some number bigger than N. Since any number’s smallest proper factor is bound to be a prime—if it wasn’t, it could be factored down into something smaller—this proves the result. If N is 5, for example, then 1 × 2 × 3 × 4 × 5 + 1 is 121, whose smallest prime factor is 11. Whichever prime you start with, you end up with a bigger one. (I shall give another proof of the infinity of primes in Chapter 7.iv, after showing you the “Golden Key.”)

Having had that point settled so early in the history of mathematics, the next thing mathematicians were naturally curious about was: Can we find a rule, a law, to describe the thinning-out? There are 25 primes up to 100. If primes were distributed perfectly evenly, there would of course be 10 times that many—250—up to 1,000. In fact there are only 168 primes up to 1,000, because of the thinning out. Why 168? Why not 158, or 178, or some other number? Is there a rule, a formula, to tell me how many primes there are less than a given number?

And there we are, back with the question that I, and Bernhard Riemann, started with: how many primes are there less than a given quantity?

III. Let’s do a little reverse engineering. I actually know the answer to that last question for quite impressively large numbers. Table 3-1 shows some.

That’s nice, but not actually terribly informative. Yes, the primes sure do thin out. If they kept up the pace set in the first 1,000, where there are 168 primes, there would be 168,000,000,000,000,000 or so in that last box. In fact there are only one-seventh that number.

In a moment I am going to perform a trick that will send a flash of light through this rather murky situation. First, though, a word about functions.

IV. A two-column table like Table 3-1 is an illustration of a function. “Function” is one of the most important concepts in all of math, the second or third most important, I should think, after “number” and possibly “set.” The main idea of a function is that some number (the one in the right-hand column) depends on some other number (the one in the left-hand column) according to some fixed rule or procedure. In the case of Table 3-1, the procedure is, “Count how many primes there are up to the number in the left-hand column.”

Another way to say the same thing is: a function is a way to turn (mathematicians say “map”) a number into another number. The function in Table 3-1 turns, or maps, the number 1,000 into the number 168—again, by way of some definite procedure.

Terms of art: Because “the number in the left-hand column” and “the number in the right-hand column” are awfully tedious things to have to keep saying, mathematicians refer to them as the “argument” and the “value” (or the “function value”) respectively. So the essence of a function is that you get a value by applying some rule or procedure to an argument.

One more key term of art. The rule that stands at the heart of a function might apply to some numbers, or some kinds of numbers, but not others. The rule, “subtract the argument from 1 and take the reciprocal,” for example, defines a perfectly respectable function— the function a mathematician would call 1 / (1 – x), which we shall look at more closely in Chapter 9.iii—but it can’t be applied to the argument “1,” since that would involve dividing by zero, which mathematics doesn’t allow. (No use to ask “What happens if I do?” You can’t. It’s against the rules. If you try, the game stops and everyone goes back to his last legal position.)

For another example, consider the function whose rule is “count the number of factors the argument has.” You find that 28 has six factors (I’m including trivial factors here), while 29 has only two. So this function turns 28 into 6; it turns 29 (or any other prime number) into 2. This is another useful and respectable function, usually written “d(N).” However, this function has a meaning only for whole numbers—really has any point only for positive whole numbers. How many factors does have? How many factors does π have? Beats me. That’s not what this function is for.

The term of art here is “domain.” The domain of a function is the numbers it can have as arguments. The function 1 / (1 – x) can have any number except 1 as an argument; its domain is all numbers except 1. The function d(N) can have any positive whole number as its

argument; that’s its domain. The domain of the function is all non-negative numbers, since negative numbers don’t have square roots (though I reserve the right to change my mind about this later in the book).

Some functions allow all numbers as their domain. The squaring function x², for example, works for any number. Any number can be squared (i.e., multiplied by itself). The same applies to any polynomial function—that is, a function whose value is got by adding and subtracting powers of the argument. Here is an example of a polynomial function: 3x⁵ + 11x³ – 35x² – 7x + 4. The domain of a polynomial is all numbers. This fact will be important in Chapter 21.iii. Most interesting functions, however, have some limits on their domain. Either there are some arguments for which the rule doesn’t work, usually because you would have to divide by zero, or else the rule only applies to certain kinds of numbers.

It’s important to understand that a table like Table 3-1 is only a sample of its function. How many primes are there less than 30,000? Less than seven million? Less than 31,556,926? Well, I could tell you by putting more rows into the table; but given that I’m trying to hold this book to a reasonable number of pages, there is obviously a limit to how much of that I can do. This table is just a sample of the function, a snapshot, with arguments I have chosen for a very deliberate purpose.

In the case of most functions, there is in fact no good way to show a function in all its glory. A graph is sometimes helpful to illustrate some particular feature of a function, but in this case a graph is pretty useless. If you try plotting Table 3-1 as a graph, you will see what I mean. My efforts to provide you with a graph of the zeta function in Chapter 9.iv will drive the point home. Mathematicians generally get a feel for a particular function by working intimately with it for a long time, observing all its features and peculiarities. A table or a graph rarely encompasses the whole thing.

V. Another thing to be noted about functions is that the important ones have names; and the really important ones have special symbols to denote them. The function I’ve sampled in Table 3-1 has the name “The Prime Counting Function” and the symbol π (N), which is pronounced “pi of N.”

Yes, I know, this is confusing. Isn’t π the ratio of a circle’s circumference to its diameter, the ineffable

3.14159265358979323846264…?

It is indeed, and this new use of the symbol π is nothing whatever to do with that. The Greek alphabet has only 24 letters and by the time mathematicians got round to giving this function a symbol (the person responsible in this case is Edmund Landau, in 1909—see Chapter 14.iv), all 24 had been pretty much used up and they had to start recycling them. I am sorry about this; it’s not my fault; the notation is now perfectly standard; you’ll just have to put up with it.

(If you have ever done any serious computer programming, you will be familiar with the concept of overloading a symbol. This use of π for two utterly different purposes is a sort of overloading of the π symbol.)

So π (N) is defined to be the number of primes up to N (inclusive, though it rarely matters, and I shall be sloppy about saying “less than” when I should say “less than or equal to”). Back to our main question: Is there some rule, some neat formula, that will give me π (N) without putting me to the trouble of counting?

Allow me to perform a small trick on Table 3-1. I am going to divide the first column by the second, the arguments by the values. I’m not aiming for terrific precision. In fact, I shall use the $6 pocket calculator I take to the supermarket. Here goes. 1,000 divided by 168 gives 5.9524; 1,000,000 divided by 78,498 gives 12.7392. Four more similar calculations give me Table 3-2.

Look closely at the values here. They go up by 7 each time. Or rather, by a number that wobbles between 6.8 and 7.0. This might not strike you as very wonderful, but a large light bulb goes on over a mathematician’s head when he sees a table like that, and a particular word comes into his mind. Let me explain.

VI. There is a certain family of functions that is terrifically important in math, the exponential functions. Chances are you know something about them. The word “exponential” is one of those that has escaped from math into ordinary language. We all hope our mutual funds will grow exponentially—that is, faster and faster.

From the point of view I have adopted here—functions illustrated by two-column tables, like Table 3-1—I can give you a loose definition of an exponential function as follows. If you pick your arguments so that they go up by regular addition from row to row, and then apply the function rule to them, and if it turns out that the resulting values go up by regular multiplication from row to row, you are looking at an exponential function. “Regular” here means that the same number is being added, or multiplied, each time.

Here’s an example, for which the rule is “Work out 5 × 5 × 5 …, where there are N fives in the expression.”

See how the arguments go up by addition of 1 each time while the values go up by a multiple of 5 each time? That’s an exponential function. The arguments go up by addition while the values go up by multiplication.

I chose the arguments to go up by adding 1 each time and shall continue to do that, just for convenience. In this particular function, this makes the values multiply by 5. Of course, there is nothing special about 5. I could pick on a function with 2 as a multiplier, or 22, or 761, or 1.05 (which would give a table showing the accumulation of compound interest at five percent), or even 0.5. Each gives me an exponential function. That’s why I started by saying “a family of functions.”

Here’s another term mathematicians are fond of: “canonical form.” When you have a situation like this, in which a certain phenomenon (in this case an exponential function) can show up in many different ways, there is generally one way mathematicians prefer to represent the whole phenomenon. So it is here. There is one exponential function mathematicians prefer above all others. If you were to take a guess at it, you might suppose it is the one in which the multiplier is 2—the simplest number to multiply by, after all. Nope. The canonical form of the exponential function has multiplier 2.718281828459045235360287…. This is another of those magic numbers, like π , that turn up all over the place in math.¹⁰ It has already turned up in this book (Chapter 1.vii). It’s irrational,¹¹ so the decimal never repeats itself, and can’t be rewritten as a fraction. The symbol for it is e, named for Leonhard Euler, of whom much more in the next chapter.

Why this number? Isn’t it an awfully clumsy number to take for your canonical form? Wouldn’t 2 be much simpler? Well, yes, it probably would, for these purposes. I can’t explain the importance of e without going into calculus, though, and I have sworn a solemn oath to explain the Riemann Hypothesis with the utter minimum of calculus. I am, therefore, just going to beg you to take on faith that e is a really, really important number, and that no other exponential function can hold a candle to this one, the function e^N.

(To 12 places of decimals.) The main principle remains, of course. The left-hand columns—the arguments—go up by adding 1 each time. As they do so, the right-hand columns—the values—are multiplied by e each time.

VII. What about the contrary situation? Suppose I find myself looking at a function whose rule is: when the arguments go up by multiplication, the values go up by addition? What kind of function is that?

Here we have entered the realm of inverse functions. Mathematicians are very keen on inverting things—turning them inside out. If y is 8 times x, what is x in terms of y? It’s y / 8, of course. Division is the inverse of multiplication. There’s a thing you like to do called squaring numbers, where you multiply a number by itself? OK, what is the inverse? If y = x², what is x equal to, in terms of y? Well, it’s the square root of y. If you know a bit of calculus, you know there’s a process called “differentiation,” that you can use to turn a function f into an-

other function g that will tell you the instantaneous rate of change of f at any argument. What’s the inverse? It’s integration. And so on. Inversion is going to be a key topic later, when I get deep into Riemann’s 1859 paper.

From the point of view of my approach here, showing a function as a table, inversion just means flipping the table round, right to left, left to right. This is actually a quick way to make trouble for yourself. Take the squaring function—probably the first non-trivial function you learned in high school. To square a number, you multiply it by itself.

(I’m assuming you remember the rule of signs¹² here, so that –3 times –3 is 9, not –9.) Now, if you flip columns, you get the inverse function.

N
9	–3
4	–2
1	–1
0	0
1	1
4	2
9	3

But hold on here. What’s the function value for argument 9? Is it –3 or 3? Couldn’t this function be rewritten like this.

N
0	0
1	1, or maybe –1
4	2, or just possibly –2
9	3, or can it also be –3?

This won’t do at all—too messy. Well … as a matter of fact, there is a mathematical theory of many-valued functions. Bernhard Riemann was a master of that theory and I shall offer a glimpse of his ideas about it in Chapter 13.v. This is not the time or the place, though, and I’m not going to have any truck with such things here. As far as I am concerned, the iron rule is, one argument, at most one value (no value at all, of course, when the argument isn’t in the function’s domain). The square root of 1 is 1; the square root of 4 is 2; the square root of 9 is 3. Does this mean I don’t acknowledge that –3 times –3 is 9? Sure I acknowledge it. I just don’t include it in my definition of the term “square root.” Here, for the time being at any rate, is my definition of a square root. The square root of N is the single non-negative number (if any) which, when multiplied by itself, gives N.

VIII. Fortunately the exponential function doesn’t give any of these problems. You can cheerfully invert it to give you a function that, when you pick arguments going up by multiplication, gives you values going up by addition. Of course, as with exponential functions, there is a whole family of inverse functions, depending on the multiplier; and as with the exponential function, mathematicians much, much prefer the one that goes up in additions of 1 when the arguments go up in multiples of e. The function you have then is called

the log function, and “log” is the word that came into the mathematician’s mind, under the illumination of the light bulb, when he saw Table 3-2. If y = e^x, then x = log y. (From which it follows, by way of straightforward substitution, that for any positive number y, y = e^{log y}, a fact I’ll pick up on later, a lot.)

In the mathematical topics relevant to this book—relevant, that is, to the Riemann Hypothesis—the log function is everywhere. I shall have much more to say about it in Chapters 5 and 7, and it will play a starring role when I actually turn the Golden Key in Chapter 19. For the time being, just take it on faith that it is a function in the sense I have just described, a really important function, and the inverse of the exponential function: If y = e^x, then x = log y.

I’m going to cut right to the chase at this point and show you the log function, but instead of going up in multiples of e, I shall let the arguments go up in multiples of 1,000. As I said, when showing a function as a table, I get to pick the arguments (and also the number of decimal places, in this case four). It’s still the same function, I swear. To help you see what’s happening, I have tacked two extra columns on at the right, the first just the right-hand column from Table 3-2, the second giving column 2’s percentage difference from column 3. The result is Table 3-3.

The following statement seems reasonable: N / π (N) is close to log N; and the larger N gets, the closer (proportionally) it gets.

Mathematicians have a special way to write this: N / π (N) ~ log N. (Pronounced “N over pi of N tends asymptotically to log N.” That wavy line is properly called a “tilde,” pronounced “til-duh.” However, in my experience, mathematicians more often refer to it as a “twiddle” sign.¹³)

If you just rearrange this according to the ordinary rules of algebra, you get:

The Prime Number Theorem

Of course, I haven’t proved this, I have just shown that it’s plausible. It is a very important result; so important that it is called “the Prime Number Theorem.” Not “a prime number theorem.” This is “the Prime Number Theorem.” Note the capital letters, which I shall use when referring to the theorem. Very often, in fact, when the context is sufficiently plain, number theorists simply write “PNT,” a practice I shall follow in this book.

IX. Finally, two consequences of the PNT, supposing it is true. To derive those consequences, let me point out that there is a sense—a logarithmic sense!—in which, when dealing with all the numbers up to some large N, most of those numbers resemble N in size. Of all the numbers from 1 to 1 trillion, for example, over 90 percent have 12 or more digits, and in that respect resemble 1 trillion (which has 13 digits) more than they resemble, say, 1,000 (which has only 4 digits).

If there are N / log N primes from 1 to N, the average density of primes in that range is 1 / log N; and since most numbers in that range are like N in size—in the very rough sense that I just described—it is fair to conclude that around N, the density of primes is 1 / log N. So it is. At the end of the first section in this chapter I counted primes in the last block of 100 numbers before 100, 500, 1,000, 1 million and 1 trillion. The counts were: 25, 17, 14, 8, and 4. The corresponding values of 100 / log N (i.e., for N = 100, 500, etc.) are, to the nearest whole numbers: 22, 16, 14, 7, and 4. Another way to say this is that in the neighborhood of a big number N, the probability of a number being prime is ~1 / log N.

By the same rough logic, we can estimate the size of the N-th prime. Consider a range of numbers from 1 to K, for some big number K. If the count of primes in that range is C, then on average we should expect to find the first of those numbers at K ÷ C, the second at 2K ÷ C, the third at 3K ÷ C, and so on. The N-th will be around NK ÷ C, and the C-th, which is to say the last in this range, will be around CK ÷ C, which means, of course, K. Now, if the PNT is true, then the count C is actually K /logK, so that the N-th prime is actually around NK ÷ (K / log K), which is to say, around N log K. Since most numbers in this range resemble K in size, I can take K and N to be interchangeable, and the N-th prime is ~ N log N. I know it looks fishy, but in fact this is not a bad estimate, and gets proportionately better and better on the twiddle principle. It predicts, for example, that the trillionth prime will be 27,631,021,115,929; in fact, the trillionth prime is 30,019,171,804,121, an 8 percent error. Percent errors at a thousand, a million, and a billion are 13, 10, and 9.

Consequences of the PNT

The probability that N is prime is ~ .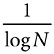

The N-th prime number is ~ N log N.

Not only are these consequences of the PNT; it is also a consequence of them. If you could mathematically prove the truth of either, the PNT would follow. Each of these results is equiponderant with (i.e., has the same weight as) the PNT, and can be considered just an alternative way of stating it. In Chapter 7.viii I shall show another, more important way to express the PNT.