Numerical Calculations of Ship Stern Flows at Full-Scale Reynolds Numbers
L.Eça (Instituto Superior Técnico, Portugal) M.Hoekstra (Maritime Research Institute, The Netherlands)
Abstract
This paper investigates the numerical calculation of ship stern flows at full scale Reynolds numbers, avoiding the use of wall-functions for the description of the near-wall flow behaviour. The calculation method is based on the Reduced Navier-Stokes equations, which allow the use of large numbers of grid nodes even with modest computer resources. The grid dependency studies show that it is possible to obtain grid independent solutions in the flow around the HSVA tanker. The comparison of the solutions at model scale and full scale Reynolds numbers for the flows around the HSVA tanker and the Mystery tanker show a strong dependence of the flowfield on the Reynolds number.
Nomenclature
1
Introduction
One of the most challenging tasks of numerical Ship Hydrodynamics is the calculation of ship stern flows. The quality assessment of the hull form and the design of the propeller will benefit from such calculations if they have sufficient predictive capability. The major part of the work on numerical stern flow prediction has been focused on the flow at model scale Reynolds numbers, 106<Re<107. The results of the Workshops of Göteborg, [1], and Tokyo, [2], give a good impression of the achievements.
Attempts to predict a stern flow at full scale Reynolds number have undoubtedly been made by several of those having successfully completed a similar calculation at model scale; but only a few have been reported. Three participants of the Göteborg Workshop of 1990, [1], and one participant of the Tokyo 1994 Workshop, [2], presented results of full scale Reynolds numbers calculations. One of the major difficulties of these calculations is to maintain stability of the numerical solution in the near-wall region. Resolution requirements impose a highly stretched grid, implying extreme grid cell aspect ratios. As a result the performance of a numerical method can deteriorate dramatically.
Ju and Patel in [3] used a two-point wall function approach to avoid the direct solution of the flow in the sublayer and buffer regions. Understandably, this alleviates the numerical difficulties considerably. However, the performance of the wall-function approach was evaluated by them on the flow around an axisymmetric body. In a complicated three-dimensional flow like a ship stern flow the restrictions of the wall function descrip-
tion are much more severe and in our opinion unacceptable in the end.
The present work investigates therefore the feasibility of performing full scale Reynolds number calculations without the use of wall functions. The numerical method is the present version of the computer code PARNASSOS, [4] to [7], which has been originally developed at MARIN and more recently extended and improved in cooperation with IST, [8]. The method is based on the reduced form of the Reynolds-averaged Navier Stokes, (RANS) equations, [9]. An eddy-viscosity algebraic turbulence model based on the formulation of Cebeci and Smith, [10], completes the mathematical model. The reduced form of the RANS equations allows the use of large numbers of grid nodes even with modest computer resources, both in memory and c.p.u.
The direct application of the no-slip condition at the wall and the use of the reduced form of the RANS equations make grid generation one of the major difficulties of full scale Reynolds number calculations. The present grid generation procedure combines elliptic and algebraic grid generation techniques. A large number of grid nodes is required in the hull-normal direction. It is important to investigate the sensitivity of the solution to the grid and to verify the grid requirements in the near-wall region.
The present paper presents the main features of the numerical method in section 2. The grid generation methodology is described in section 3. The grid dependency studies and an investigation of the influence of the distance of the first grid node to the wall in the direct application of the no-slip condition follow in section 4. Also included in section 4 is a comparison between numerical predictions at full scale and model scale Reynolds numbers for the two test cases of the Tokyo Workshop, [2]: the HSVA tanker and the Mystery tanker. The conclusions of the paper are summarized in section 5.
2
Computational Method
2.1
Mathematical Formulation
The Reynolds-averaged Navier-Stokes equations for steady flow of an incompressible fluid consist of equations expressing mass and momentum conservation, supplemented with a turbulence model. The conservation equations are written here for a general curvilinear coordinate system ξi (alternatively denoted as the ξ, η, ζ system) in contravariant form with the cartesian velocity components, Ui, as the dependent variables:
(1)
(2)
with
(3)
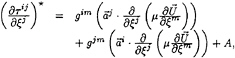
(4)
and
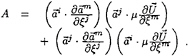
(5)
The tensorial summation convention applies; ![]() are the contravariant base vectors:
are the contravariant base vectors:
p is the pressure, ρ the fluid mass density, µ the fluid effective viscosity, ![]() is the Jacobian of the transformation between the two systems and gij is the contravariant metric tensor. A partial parabolisation is obtained by choosing ξ1 as the main-stream direction and by neglecting diffusion in that direction, i. e. the terms with j=1 in the viscous terms of momentum equations (2). The elliptic character of the equations is retained in the pressure field. All diffusion terms are dropped in the momentum equation in the normal direction. The present set of equations is classified by Rubin et al. in [9] as the Reduced Navier-Stokes (RNS) equations.
is the Jacobian of the transformation between the two systems and gij is the contravariant metric tensor. A partial parabolisation is obtained by choosing ξ1 as the main-stream direction and by neglecting diffusion in that direction, i. e. the terms with j=1 in the viscous terms of momentum equations (2). The elliptic character of the equations is retained in the pressure field. All diffusion terms are dropped in the momentum equation in the normal direction. The present set of equations is classified by Rubin et al. in [9] as the Reduced Navier-Stokes (RNS) equations.
The fluid effective viscosity, µ, is obtained with an isotropic eddy-viscosity algebraic turbulence model, [10].
The use of the RNS equations implies that a physical meaning is attached to the grid, since diffusion is neglected in the streamwise direction, while that direction is determined by the grid. To take advantage of the roughly flow-conforming
coordinate system ξ, η, ζ, the grid-aligned physical components of the velocity vector, V(i), are chosen as the velocity dependent variables. These are defined by
(6)
where
(7)
The fourth dependent variable is the pressure, used without geometrical scaling.
The conversion from the cartesian to the grid-aligned physical velocity components is achieved with the following relations:
(8)
But the form of the equations as written in (2) is maintained as the basis for the discretization. This procedure ensures that the discrete equations can reproduce a uniform flow exactly, [11].
The flow solution is obtained by solving the continuity and momentum equations with the appropriate boundary conditions. In matrix notation the velocity component in the normal direction, V(2), is associated with the continuity equation and the pressure with the ξ2 momentum equation. This is an alternative for the replacement of the continuity equation by a Poisson equation for the pressure or for the introduction of artificial compressibility. The coupling of the equations is maintained in the solution process.
2.1.1
Boundary Conditions
The flow around a ship hull has six boundaries. The inlet station, the outlet station, the free-surface, the symmetry plane of the ship, the ship surface and the external boundary. In the present calculations, the three velocity components at the inlet station were prescribed with standard boundary layer profiles, based on given momentum thickness and wall friction coefficient [12]. The streamwise pressure gradient was set equal to zero at the outlet boundary. Symmetry boundary conditions are applied at the symmetry plane of the ship but also at the free-surface. The latter means that the formation of gravity waves is left out of account. On the ship surface the three velocity components are set equal to zero and the flow is calculated down to the surface, without wall-functions. At the external boundary the tangential components of the velocity and the pressure are prescribed by a potential flow calculation, [13].
2.1.2
Grid Singularities
At a grid singularity, (![]() or
or ![]() ), the metric relations of the coordinate transformation are not applicable. This means that the solution at grid singularities cannot be obtained with the same procedure as used for non-singular points. In the present approach, grid singularities are dealt with explicitly. The cartesian velocity components and the pressure at a grid singularity are calculated with a different system of equations and substituted in the discretized equations as known values. The cartesian velocity components and the pressure at the singular node are obtained by a weighted1 mean of the surrounding nodes in a previous iteration2.
), the metric relations of the coordinate transformation are not applicable. This means that the solution at grid singularities cannot be obtained with the same procedure as used for non-singular points. In the present approach, grid singularities are dealt with explicitly. The cartesian velocity components and the pressure at a grid singularity are calculated with a different system of equations and substituted in the discretized equations as known values. The cartesian velocity components and the pressure at the singular node are obtained by a weighted1 mean of the surrounding nodes in a previous iteration2.
2.2
Numerical Solution
2.2.1
Discretization
The continuity and contravariant momentum equations, (1) and (2), after replacement of the cartesian velocity components by the grid-aligned physical velocity components with the relations (8), are discretized in a single-block regular grid by a finite-difference approximation. The discretization procedure is the same as the one used in the original code PARNASSOS, [4] to [7]. The main characteristics of this procedure are summarized below:
-
All the variables are defined on the grid nodes, (i,j,k)3; grid staggering is not used.
-
Newton linearization is applied to the convective terms.
-
The streamwise convective terms are dropped at points where the streamwise velocity is negative.
-
The momentum equation in the ξ and ζ directions are discretized at the nodal points (i,j,k).
|
1 |
The weights are calculated from the distance to the singularity of the nodes involved. |
|
2 |
The solution procedure has to be iterative due to the non-linearity of the equations. |
|
3 |
The indices refer to the ξ, η and ζ direction, respectively. |
-
The momentum equation in the normal direction, η, is discretized at
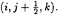
-
The continuity equation is discretized at
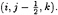
A detailed description of the implementation of the finite-difference approximations can be found in [8].
2.2.2
Iterative Procedure
The solution is obtained iteratively by a space-marching process. Two iteration cycles can be distinguished: the local and the global iteration process.
The local iteration process refers to the solution of the flow at a streamwise station where all the grid nodes have the same main-stream coordinate ξ. The solution is obtained simultaneously for all the variables with a Coupled Strongly Implicit Procedure (CSIP) [14]. The non-linearity of the differential equations and the incomplete factorization of the CSIP require an iterative solution.
The discretized equations at a streamwise station where all the grid nodes have the same main-stream coordinate ξ, include the pressure field at the downstream station. This implies that in order to obtain the solution by a space-marching process in the main-stream direction, the pressure field at the downstream stations has to be taken from a previous sweep. The downstream marching process has to be repeated until the changes in the pressure field between consecutive sweeps are negligible. Thus the global iteration process involves the evaluation of the solution in repeated sweeps from the inlet to the outlet boundary of the computational domain. To increase the convergence rate of this process each downstream sweep is followed by an upstream sweep to update the pressure field. The two sweeps form a predictor-corrector method for the pressure, which is constructed by adding a quasi-time derivative to the momentum equations, [7].
2.2.3
Grid Sequencing
Streamwise Direction
To improve the pressure field convergence a multiple stepsize is used in the initial global iteration sweeps to allow a rapid approach of the correct pressure level, [6]. In the initial sweep only every 8th grid node4 of each ξ line is used. The multiple stepsize is subsequently reduced to 4, 2 and finally 1. The changes in the multiple stepsize are controlled by the maximum pressure coefficient difference between consecutive sweeps, (ΔCp)max, with
ΔCp=Cpn–Cpn–1, (9)
where the superscript n indicates the number of the sweep of the global iteration process and
(10)
Girthwise Direction
The technique used for the girthwise direction is similar to the one used in the streamwise direction and has the same purpose. The use of a grid sequencing technique in the girthwise direction also increases the convergence rate of the CSIP in the initial global iteration sweeps, when the initial approximation at each streamwise station is still too far from the final solution. The reduction of the stepsize in girthwise and streamwise directions is simultaneous.
Normal Direction
The grid sequencing technique applied in the streamwise and transverse directions is related to the global iteration process. A different grid sequencing technique is applied in the normal direction. Grid sequencing in the normal direction is mainly required by the clustering of grid lines close to the symmetry plane of the wake, imposed by the application of the no-slip condition at the ship surface. Therefore, the grid sequencing technique in the normal direction is related to the local iteration process.
The CSIP is applied at a streamwise station where all the grid nodes have the same ξ-coordinate. The boundary conditions at the ζ-line η=0 (j=1) may include the following situations :
-
Wake station. The nodes are all on the symmetry plane of the wake and symmetry conditions apply to all the nodes.
-
Ship station. The nodes are all on the ship surface and the no-slip condition applies to all the nodes.
|
4 |
This implies that the total number of nodes in the streamwise direction has to be a multiple of 8 plus 1. |
-
Mixed station. The no-slip condition applies to part of the nodes and symmetry conditions apply to the others.
In a wake station, the essential parameter to control the convergence rate of the CSIP close to the symmetry plane of the wake is the distance between the grid nodes. In this case, the use of a multiple stepsize is not a good option. For it would mean that the multiple stepsize required for grid distance enlargement close to the symmetry plane yields an unacceptably large distance between grid nodes close to the outer boundary.
The present approach is to perform an initial calculation of the CSIP in a coarser grid where the distance between grid nodes in a given η line is larger than a specified distance. When the calculation process proceeds to the fine grid, the initial approximation for the solution on the fine grid is obtained by linear interpolation of the solution on the coarse grid. There are no restrictions on the number of grid nodes to be used in the normal direction with this grid sequencing technique.
In the ship stations grid sequencing is not applied because a solution on a coarse grid does not yield a good initial approximation for the solution on the fine grid, due to the no-slip boundary condition.
A compromise has to be made at a streamwise station where the ship surface and the wake symmetry plane coexist. Grid sequencing is required by the wake boundary condition but it is undesirable at η lines where the no-slip boundary condition applies. In these mixed stations, we apply a grid sequencing technique as for wake stations. However, the specified minimum distance between grid nodes is chosen one order of magnitude smaller than in the wake stations. Furthermore, we do not apply grid sequencing in the global iteration sweeps performed with multiple stepsize factors 8 and 4.
3
Grid Generation
If the RNS equations are chosen as the basis for a numerical simulation of ship stern flows the computational grid must be roughly flow conforming. For a simulation at full scale Reynolds numbers the distance between grid lines close to the ship surface may be of the order of 10–9 of the ship length L. Furthermore, the grid lines should be nearly orthogonal to the ship surface in the near-wall region, which may be troublesome in ship stern cross-sections including both concave and convex regions. All these requirements together mean that grid generation in such a numerical calculation is a complex problem, but at the same time a crucial factor for its success.
In order to be able to deal with all the requirements of an acceptable grid, the present grids are generated in two steps:
-
Generate a basis grid using a 3D elliptic grid generator.
-
Apply grid line stretching along the normal, η, grid lines with an algebraic technique.
The present 3D grid generator, [15], is based on the elliptic generating system incorporated in the EAGLE code, [16]. The method allows the specification of the coordinates of all the boundary nodes and the grid line pattern is defined by the so-called control functions, which are calculated iteratively to obtain the following properties:
-
Orthogonality at the boundaries.
-
A specified distance of the first grid node to the boundary.
-
An interior grid line spacing that reflects the boundary point distribution.
The present elliptic generating system follows Thompson's description, [17], of the so-called GRAPE approach, [18].
The non-linear terms of the control function that guarantee grid line orthogonality at the boundaries are inversely proportional to the grid line spacing. This means that it is extremely difficult, if not impossible, to compute an acceptable grid if the desired near-wall grid line distance is imposed directly on the 3D elliptic grid generator. Therefore, we generate a basis grid using moderate grid line stretching in the normal direction.
The final grids are obtained by carrying out step 2: stretching of the basis grid with an algebraic interpolation technique. The interpolation is performed along the η lines using three cubic splines, one for each cartesian coordinate of the grid nodes involved. The stretching functions proposed by Vinokur in [19] are used. For all η lines in a grid plane ξ=constant the same stretching is applied so that the deviations from orthogonality of the final grid are similar to the ones of the basis grid. It has been found that the number of grid nodes of the basis grid in the vicinity of the boundaries η=0 and η=1 must be sufficient to avoid oscillations in the spline representation of the η grid lines.
4
Results
4.1
General
The flow around the sterns of the HSVA tanker and of the Mystery tanker were selected for the present studies. These two sterns are the test cases of the Göteborg and Tokyo Workshops, [1] and [2]. The calculations were performed at full scale Reynolds number, 2.0×109, and at model scale Reynolds number, 5.0×106. The Reynolds number is defined by
where U∞ is the undisturbed flow velocity, L is the ship length, and v is the kinematic viscosity of the fluid.
A cartesian coordinate system is introduced with the x axis along the undisturbed stream, the z axis vertical positive pointing upwards and y completing a right-hand system. The origin of the coordinate system is located on the foreword perpendicular at the ship symmetry plane on the free surface. All the variables presented in the results are made non-dimensional using U∞ and L as the velocity and length reference scales.
The convergence criterion used in the global iteration process of all the calculations performed was a minimum pressure coefficient difference, (ΔCp)max, between consecutive sweeps of 5.0× 10–3. In the local iteration process, CSIP, the convergence criteria was a maximum difference between physical components of the contravariant velocity components of 1.0×10–4U∞ and a maximum Cp difference between iterations of 2.0×10–5. The maximum number of iterations allowed for the CSIP at each streamwise station was 51.
In the present calculations the boundaries of the computational domain are located as follows:
-
The inlet boundary is a x=constant plane at x=0.65.
-
The outlet boundary is a x=constant plane at x=1.20.
-
The external boundary is an elliptic surface with y and z axis of approximately 0.19 and 0.15.
-
The remaining boundaries are the free surface, plane z=0, the symmetry plane of the ship, plane y=0, and the ship surface.
The results of the present calculations are plotted at x=constant planes and on the ship surface. The local values of all the variables at the x constant planes, which do not coincide with grid nodes, are calculated by linear interpolation along the streamwise grid lines. The limiting streamlines are obtained by a predictor-corrector integration of the wall shear-stress.
All the calculations were performed on a DEC Alpha 7620 with 64 bytes precision. The program requires 65 Mbytes of RAM and with the present convergence criteria the c.p.u. time is approximately 0.05 seconds per grid node.
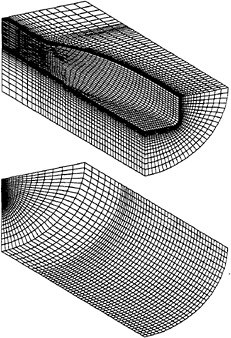
Figure 1: Illustration of the grid for the calculation of the flow around the HSVA tanker.
4.2
Grid Dependency Studies
A limited number of grid dependency studies was performed for the flow around the HSVA tanker. A reference grid was adopted which has 97×149×57 grid nodes. The streamwise step size in the stern region is approximately equal to 0.005L. In the wake region the streamwise stepsize is increased up to 0.014L. The grid has an
equally spaced boundary point distribution in the girthwise direction.
The near-wall grid density is monitored by the maximum y+ distance of the first grid node to the wall,
where uτ is the skin friction velocity. The ![]() can not be known a priori, because it depends on the flow solution. This means that the stretching required to obtain a given value of
can not be known a priori, because it depends on the flow solution. This means that the stretching required to obtain a given value of ![]() is estimated from a previous calculation. The reference grid has
is estimated from a previous calculation. The reference grid has ![]() which corresponds to a minimum grid node distance of 10–9 L.
which corresponds to a minimum grid node distance of 10–9 L.
The grid boundary point distribution of the reference grid is illustrated in figure 1, where only half of the grid nodes in each direction are plotted.
The grid dependency studies concerned variations of the number of grid nodes in the normal direction. On the one hand this number was changed, keeping approximately the same near-wall spacing; on the other hand, the near-wall grid node density was systematically changed, keeping the discretization in the outer region equal.
4.2.1
Outer region grid refinement
Calculations were performed with three different numbers of grid nodes in the normal direction, nη, 105, 125, and 149, keeping approximately the same value of ![]() in all the grids.
in all the grids.
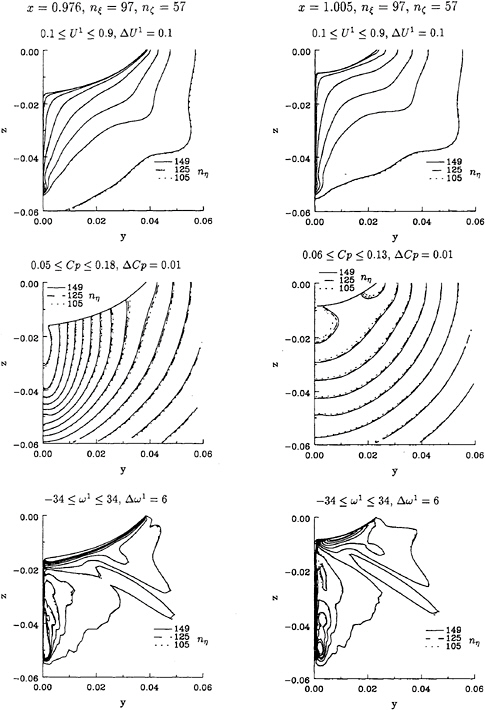
The surface pressure distribution and the limiting streamlines of the three calculations are plotted in figure 2. The surface isobars and limiting streamlines are graphically almost coincident. Only the solution with nη=105 grid nodes shows some small deviations at the end of the stern.
Figure 3 presents the comparison of the isolines of axial velocity, U1, pressure coefficient, Cp, and axial vorticity, ω1, at x=0.976 and x=1.005. The isolines of axial velocity of the three calculations are almost undistinguishable; there are insignificant differences between the solutions in the outer region only. The differences between the three solutions are better visible in the isobars, where in particular the solution obtained with nη=105 deviates; the differences between the solutions with nη=125 and nη=149 are small. The axial vorticity isolines of the three calculations are almost identical. Bearing in mind that the axial vorticity is computed by numerical differentiation in grids with different grid nodes location, the differences between the axial vorticity isolines are not significant. The transverse velocity fields of the three calculations at these two planes are identical and the maximum transverse velocities of the three calculations differ less than 0.1% of U∞.
It should be mentioned that the performance of the CSIP is getting worse with the increase of the number of grid nodes per streamwise station. This deterioration becomes rather serious for discretizations finer than a critical value. A test run made with nη=175 showed that 51 iterations of the CSIP are not sufficient to satisfy the present convergence criteria, which means that a larger number of iterations must be used in the CSIP to obtain the same precision. Therefore, the c.p.u. per grid node with nη=175 is much larger than the one obtained for nη=105, nη=125 and nη=149. However, the present results suggest that there is no need to increase the number of grid nodes in the normal direction beyond 149.
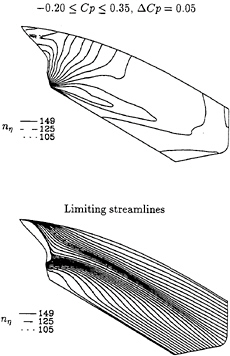
Figure 2: HSVA tanker, Re=2.0×109. Comparison of surface pressure distribution and limiting streamlines obtained with different numbers of grid nodes in the normal direction.
4.2.2
Near-Wall Discretization
The required grid node density in the near-wall region to obtain a grid independent solution was investigated keeping an approximately constant grid node density in the outer region. Three calculations were performed with the following grids: nη=139 and ![]() nη=149 and
nη=149 and ![]() and nη=159 and
and nη=159 and ![]()
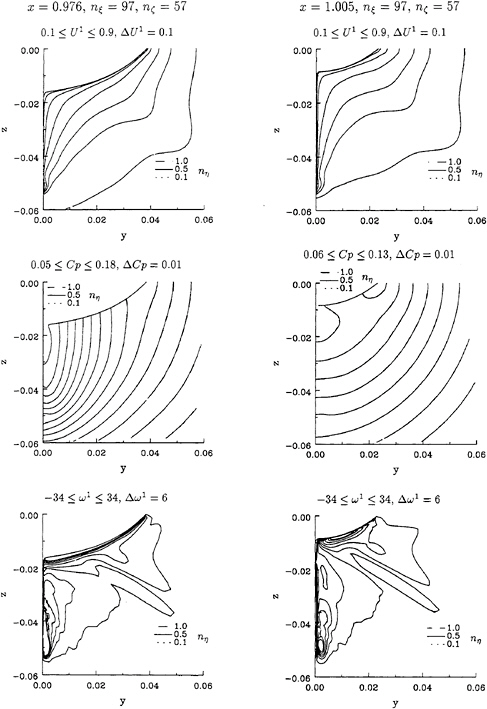
The surface pressure distribution and the limiting streamlines of the three calculation are plotted in figure 4. The surface isobars and limiting streamlines are graphically coincident.
Figure 5 presents the comparison of the isolines of axial velocity, U1, pressure coefficient, Cp, and axial vorticity, ω1, at x=0.976 and x=1.005. The three solutions are graphically coincident. Only the axial vorticity isolines show some very small differences, which are not significant. The transverse velocity fields of the three calculations at these two planes are also identical and the maximum transverse velocities of the three calculations differ less than 0.05% of U∞, which is of the order of magnitude of the present convergence criteria.
These results suggests that it is possible to obtain a grid independent solution of the near-wall region in a ship stern flow at full scale Reynolds number.
4.3
Comparison of Solutions at Full Scale and Model Scale Reynolds Numbers
The flow around the HSVA tanker and the Mystery tanker were calculated at full scale and model scale Reynolds numbers, 2.0×109 and 5.0×106, respectively. The calculations at Re=2.0×109 were performed on grids with 97×149×57 grid nodes. The grids of the model scale calculations have 97×105×57 grid nodes.
4.3.1
HSVA tanker
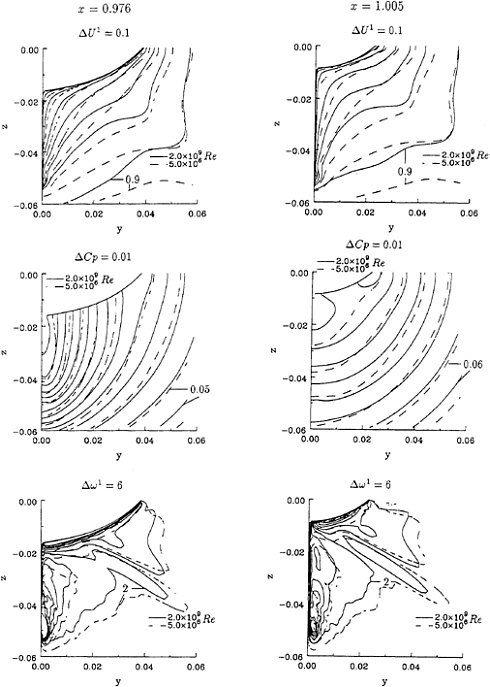
The isolines of U1, Cp and ω1 of the two calculations are plotted in figure 6. Not surprisingly, the isolines of axial velocity show a strong reduction of the thickness of the boundary layer region when the Reynolds number is increased. In the present calculation the typical ‘hook' shape of the U1 contours is not reproduced, which was to be expected with the present turbulence model. The maximum pressure at the stern increases with Reynolds number and so does the axial vorticity.
Figure 7 presents the transverse velocity fields at x=0.976 and x=1.005. The core position of the bilge vortex moves to the symmetry plane with increasing Re. The cross-stream velocities at Re=2.0×109 are larger than at Re=5.0×106.
The surface pressure distribution of the two flows is compared in figure 8. In general the pressure distribution becomes less smooth with higher Re; peaks are higher, troughs deeper. Figure 9 presents the limiting streamlines of the two calculations. Most striking are the difference in the location where a confluence of limiting streamlines occurs, that is the location from which the bilge vortex originates. It has been found from additional calculations at intermediate Reynolds numbers that this upward shift of the line of confluence is systematic. There is also a slight delay of streamwise flow separation at high Re.
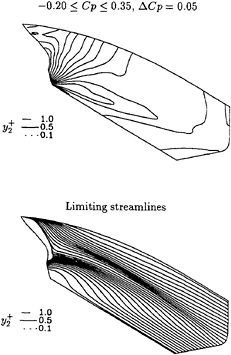
Figure 4: HSVA tanker, Re=2.0×109. Comparison of surface pressure distribution and limiting streamlines obtained with different near-wall grid nodes density.
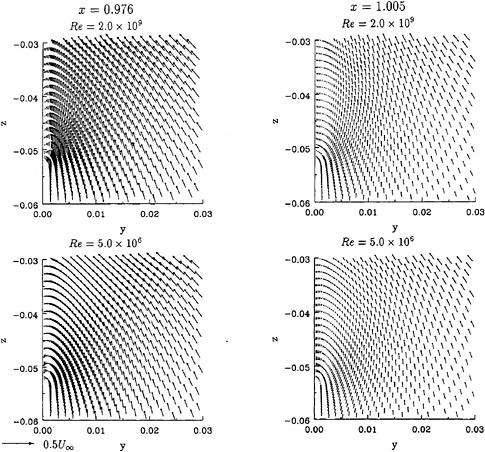
Figure 7: HSVA tanker. Transverse velocity fields of calculations performed at full scale and model scale Reynolds numbers.
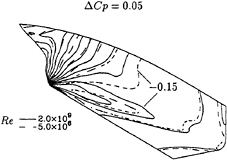
Figure 8: HSVA tanker. Comparison of surface pressure distribution for calculations performed at full scale and model scale Reynolds numbers.
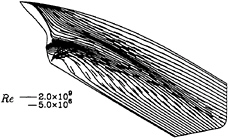
Figure 9: HSVA tanker, Re=2.0×109. Comparison of limiting streamlines for calculations performed at full scale and model scale Reynolds numbers.
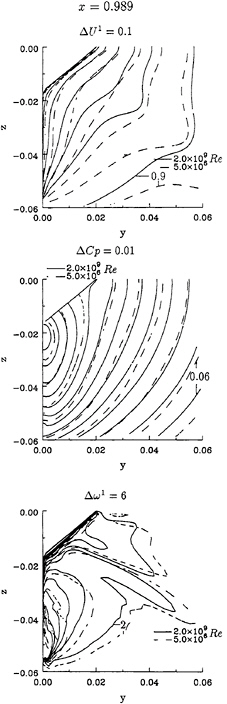
Figure 10: Mystery tanker. Comparison of calculations performed at full scale and model scale Reynolds numbers.
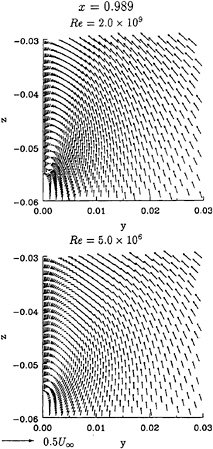
Figure 11: Mystery tanker. Transverse velocity fields of calculations performed at full scale and model scale Reynolds numbers.
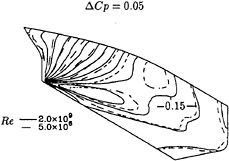
Figure 12: Mystery tanker. Comparison of surface pressure distribution for calculations performed at full scale and model scale Reynolds numbers.
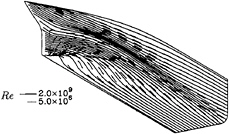
Figure 13: Mystery tanker, Re=2.0×109. Comparison of limiting streamlines for calculations performed at full scale and model scale Reynolds numbers.
4.3.2
Mystery tanker
The comparison between results at model scale and full scale Reynolds numbers is presented in figures 10 to 13. In general, the comparison of results at model and full scale Reynolds numbers is similar to the one obtained for the HSVA tanker.
The isolines of U1, Cp and ω1 are plotted in figure 10, where the decrease of the boundary layer thickness with the increase of Reynolds number is clear. The transverse velocity fields at x=0.989 are presented in figure 11. The bilge vortex location of the two calculations is not equal and the cross-stream velocities are larger at Re=2.0×109 than at 5.0×106. The isobars on the ship surface of the two calculations are compared in figure 12. The effect of the Reynolds number in the surface pressure distribution is evident.
The limiting streamlines of the two calculations are plotted in figure 13. There is a significant difference between the two flows. At model scale, a small streamwise flow separation region is predicted at the end of the stern close to the free surface. No streamwise flow separation is predicted at full scale Reynolds number.
5
Conclusions
The feasibility of the calculation of ship stern flows at full scale Reynolds numbers with direct application of the no-slip condition at the hull surface has been proven. The numerical method with which this result has been obtained is based on the Reduced form of Reynolds averaged Navier-Stokes equations, which allows the use of large numbers of grid nodes, required by the calculation of the near-wall region, at acceptable computing time.
The grid dependency studies performed for the flow around the HSVA tanker suggest that it is possible to obtain a grid-independent solution without the use of wall-functions. The number of grid nodes required in the normal direction is within the acceptable limits of the present method. This is fortunate because further increase of the number of grid nodes per streamwise station may require a more robust—but also more expensive—solver.
In the present calculations for the HSVA tanker, it was found that the solution was independent of the near-wall grid density for distances of the first grid node to the wall smaller than ![]()
The comparison of full scale and model scale Reynolds numbers calculations for the HSVA tanker and the Mystery tanker confirmed a strong dependence of the flow field at the end of the stern on the Reynolds number. The limiting streamlines showed a systematic change in position of the confluence of limiting streamlines with increasing Reynolds number. On the two test ships streamwise flow separation was delayed at high Re.
References
[1] Larsson L., Patel V.C., Dyne G. (eds.)— Ship Viscous Flow.—Proceedings of 1990 SSPA-CTH-IIHR Workshop, Flowtech International AB, Research Report No 2, Gothenburg, June 1991.
[2] Proceedings of CFD Workshop Tokyo 1994, Ship Research Institute Tokyo , March 1994.
[3] Ju S., Patel V.C.—Stern Flows at Full-Scale Reynolds Numbers.—Journal of Ship Research, Vol. 35, No 2, June 1991, pp. 101–103.
[4] Raven H.C., Hoekstra M.—A Parabolised Navier-Stokes Solution Method for Ship Stern Flow Calculations.—2th International Symposium on Ship Viscous Resistance, Göteborg Sweden, March 1985.
[5] Hoekstra M., Raven H.C.—Application of a Parabolised Navier-Stokes Solution System to Ship Stern Flow Computation .—Osaka International Colloquium on Ship Viscous Flow, Osaka Japan, October 1985.
[6] Hoekstra M., Raven H.C.—Ship Boundary Layer and Wake Calculation with a Parabolised Navier-Stokes Solution System. —4th International Conference on Numerical Ship Hydrodynamics”, Washington D.C., 1985.
[7] Hoekstra M.—Recent Developments in a Ship Stern Flow Prediction Code.— 5th International Conference on Numerical Ship Hydrodynamics, Hiroshima, September 1989.
[8] Eça L.—Numerical Solution of the Parabolised Navier-Stokes Equations for Incompressible Tip Vortex Flows .—PhD Thesis, Instituto Superior Técnico, Lisbon, March 1993.
[9] Rubin S.G., Tannehill J.C.—Parabolized/Reduced Navier-Stokes Computational Techniques.—Annual Review of Fluid Mechanics, Vol. 24, 1992, pp. 117–144.
[10] Cebeci T., Smith A.M.O.—Analysis of Turbulent Boundary Layers.—Academic Press. November 1984.
[11] Eça L, Hoekstra M.—Discretization of the Parabolised Navier-Stokes Equations.— First European Computational Fluid Dynamics Conference, Brussels, September 1992.
[12] Hoekstra M.—Generation of Initial Velocity Profiles for Boundary Layer Calculations— Marin Report No 50028–1-SR, March 1980.
[13] Raven H.C.—Berekening van de potentiaal-stroming rond draagvlakken met het programma DAWSON—Marin Report No 50501–1-RD, May 1985.
[14] Rubin S.G.—Incompressible Navier-Stokes and Parabolised Navier-Stokes Formulations and Computational Techniques .— Computational Methods in Viscous Flow, Vol. 3 in the series Recent Advances in Numerical Methods in Fluids (ed. Habashi) Pineridge Press, 1984.
[15] Eça L.—Grid Generation with Systems of Partial Differential Equations (in Portuguese), IV National Meeting of Computational Mechanics, Lisbon, April 1995.
[16] Thompson J.F.—Composite Grid Generation Code for General 3-D Regions—the EAGLE code—AIAA Journal, Vol. 26, March 1988, pp. 271–272.
[17] Thompson J.F.—A General Three-Dimensional Elliptic Grid Generation System on a Composite Block Structure.— Computer Methods in Applied Mechanics and Engineering, Vol. 64, 1987, pp. 377–411.
[18] Sörenson R.L.—Grid Generation by Elliptic Partial Differential Equations for a Tri-Element Augmentor-Wing Airfoil —Numerical Grid Generation, ed. Thompson J.F., North-Holland, 1982.
[19] Vinokur M.—On One-Dimensional Stretching Functions for Finite-Difference Calculations.—Journal of Computational Physics, Vol. 50, 1983, pp. 215–234.