Spray Formation at the Free Surface of Turbulent Bow Sheets
Z.Dai, L.-P.Hsiang, G.Faeth (University of Michigan, USA)
ABSTRACT
An experimental study of transitions at the free surface of turbulent liquid wall jets in still air at normal temperature and pressure is described. Measurements involved initially nonturbulent annular wall jets with the growth of a turbulent boundary layer along the wall initiated by a trip wire. Pulsed photography, shadowgraphy and holography were used to observe the location of the onset of roughened liquid surfaces, the location of the onset of turbulent primary breakup, and drop sizes at the onset of turbulent primary breakup, along the free surface of the liquid wall jets. Test conditions included several liquids (water, ethyl alcohol and various glycerol mixtures), liquid gas density ratios of 680–980, wall jet Reynolds numbers of 10,000 –600,000 and Weber numbers of 4,000–53,000, at conditions where direct effects of liquid viscosity on turbulent primary breakup were small. It was found that transitions to roughened liquid surfaces and turbulent primary breakup were caused by turbulence originating in the liquid phase, while direct effects of aerodynamic forces at the liquid surface were small. Transition to a roughened liquid surface could be correlated by associating the thickness of the growing turbulent boundary layer along the wall with the thickness of the wall jet. Drop sizes at the onset of turbulent primary breakup could be correlated by equating the surface energy required to form a drop to the kinetic energy of an eddy of corresponding size. Finally, the location of the onset of turbulent primary breakup could be correlated in terms of the distance convected at the mean velocity of the wall jet for a time needed to initiate the Rayleigh breakup of the ligaments protruding from the liquid surface that produce drops at the onset of turbulent primary breakup.
NOMENCLATURE
|
b |
annulus width |
|
Cr |
empirical constant for roughened liquid surface |
|
Csi |
empirical constant for SMD at onset of breakup |
|
d |
round jet diameter |
|
drod |
diameter of center rod of annulus |
|
D |
hydraulic diameter of wall jet, 4b(1+b/drod) |
|
ep |
volume-averaged ellipticity |
|
k |
trip wire height |
|
ℓ |
characteristic eddy size |
|
ℓK |
Kolmogorov length scale |
|
L |
passage length, Rayleigh breakup length |
|
OhD |
Ohnesorge number, µf/(ρfDσ)1/2 |
|
ReD |
wall jet Reynolds number, uoD/vf |
|
Rex |
boundary layer Reynolds number, uox/vf |
|
SMD |
Sauter mean diameter |
|
u |
streamwise velocity |
|
u* |
friction velocity, (τw/ρf)1/2 |
|
v |
radial velocity |
|
vℓ |
radial velocity associated with eddy of size ℓ |
|
WefΛ |
Weber number, ρfuoΛ/σ |
|
x |
streamwise distance |
|
δ |
boundary layer thickness |
|
Λ |
radial integral length scale |
|
µ |
molecular viscosity |
|
v |
kinematic viscosity |
|
σ |
surface tension |
|
τi |
characteristic drop formation time |
|
τw |
wall shear stress |
|
Subscripts |
|
|
f |
liquid-phase property |
|
g |
gas-phase property |
|
i |
at point of breakup initiation |
|
k |
at the location of trip wire |
|
r |
at the point of rough surface initiation |
|
t |
transition from laminar to turbulent boundary layer |
|
w |
wall condition |
|
o |
jet exit condition |
|
Superscripts |
|
|
(ˉ) |
time-averaged mean property |
|
(ˉ)′ |
time-averaged rms fluctuating property |
INTRODUCTION
An experimental investigation concerning aspects of the generation of sprays by the bow waves (or bow sheets) of ships is described. This flow is important as a representative spray formation process of the marine environment, which contributes to the structure of ship-generated waves and the electromagnetic scattering properties (e.g., the photographic and radar signatures) of vessels. The overall objectives of the investigation were to make new measurements of several properties associated with the sprays produced by bow sheets, emphasizing transitions at the free surface of attached turbulent bow sheets (or turbulent wall jets). This work included measurements of the onset location of roughened liquid surfaces, and the properties (drop sizes and location) of the onset of primary drop breakup (turbulent primary breakup) along the liquid surface. Finally, the new measurements were interpreted and correlated using phenomenological theories.
Bow sheet/spray flows are complex and involve a number of turbulence/surface interactions and spray formation mechanisms. This complexity has prevented complete understanding of bow sheet/spray flows; nevertheless, there is general agreement about the qualitative features and spray forming mechanisms of bow sheets (1–3). In particular, flows associated with chutes, spillways, plunge pools, hydraulic jumps, open water waves and jets exhibit similar features of spray formation. In general, the mechanism appears to involve the propagation of vorticity (especially turbulence) to the liquid surface, or its development along the surface, with the subsequent appearance of a turbulence-wrinkled interface between the liquid and gas and eventually the formation of drops due to turbulent primary breakup at the liquid surface.
An important issue concerning the transitions of turbulent bow sheets is the origin of the turbulence near the liquid surface, e.g., whether this turbulence mainly is caused by motion along the bow surface or whether it mainly results from aerodynamic forces at the liquid surface. This issue was partly addressed during the present study by observing round water jets injected into still air at normal temperature and pressure (NTP), with large jet Reynolds numbers (ReD >120,000) and a variety of passage configurations. In all cases, a large contraction (roughly 100:1 and shaped according to Smith and Wang (4)) followed by boundary layer removal, was used to generate a uniform nonturbulent flow. This flow then entered round constant diameter passages having various lengths in order to study the effect of turbulence developed in the passage on liquid jet properties. Some typical pulsed shadowgraphs of the flow near the jet exit for short and long passages are illustrated in Fig.1. For the short passage, L/d=0.15, the flow remains essentially uniform and nonturbulent at the jet exit; this

Fig. 1. Pulsed shadowgraphs of round nonturbulent and turbulent liquid jets in still air.
yields a liquid jet that has a smooth surface with no tendency to break up into drops over the range of jet lengths that could be observed In contrast, for L/d=41, the passage is sufficiently long to obtain fully-developed turbulent paper flow at the exit (5,6); this immediately yields a liquid jet that has a roughened liquid surface. These results provide rather strong evidence that turbulence generated by motion along solid surfaces, rather than by relative motion at the gas/liquid interface, causes liquid surface roughness and primary breakup with drops at liquid surfaces in air at NTP when the liquid has similar relative velocities with respect to both the solid surface and the air.
Based on the notion that turbulence causing liquid surface roughness and primary breakup along liquid surfaces in bow sheets originates from liquid motion along the bow surface, the resulting spray formation processes typical of most bow sheets are sketched in Fig.2. The reference frame used in this figure involves an observer on the ship so that the bow sheet moves over the surface as a plane wall jet before detaching at some point into a plane free jet. Notably, the air adjacent to the liquid surface generally is moving at nearly the same velocity as the liquid, which further reduces the potential for significant aerodynamic effects at the liquid surface, compared to the conditions illustrated in Fig.1. The liquid flow along the surface then involves a relatively inconsequential laminar boundary layer, followed by a growing turbulent boundary layer. The onset of liquid surface roughness
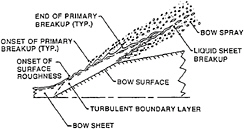
Fig. 2. Sketch of bow-sheet and bow-spray transitions.
is thought to correspond to conditions where the outer boundary of the turbulent boundary layer reaches the liquid surface, however, existing studies (1–3) have not yet quantified this condition in terms of boundary layer properties. Subsequently, primary breakup can begin along the surface of the turbulent liquid and can continue in the free jet region, ultimately causing the bow sheet to break up as a whole. Past work treating such turbulent primary breakup processes will be considered next.
The existence of turbulent primary breakup has been recognized for some time (1–3). Round turbulent liquid jets injected into still gases, or liquid free jets, generally have been used to study turbulent primary breakup. The early studies of DeJuhasz et al. (7) and Lee and Spencer (8,9) showed that liquid turbulence properties at the jet exit affected the atomization, breakup and mixing properties of liquid jets in still gases at NTP. Next, Grant and Middleman (10), Phinney (11) and McCarthy and Malloy (12) observed that jet stability and the onset of breakup were affected by turbulence at the jet exit as well. Finally, in a series of experiments involving coflowing and counterflowing gas/liquid round jets at NTP, Hoyt and Taylor (13–15) provided substantial evidence that aerodynamic effects did not have a large influence on turbulent primary breakup, as discussed in connection with Fig.1.
Several recent studies of the properties of turbulent primary breakup were completed in this laboratory, based on observations of round liquid jets injected into still gases with fully-developed turbulent pipe flow at the jet exit (16–25). These studies involved pulsed shadowgraphy and holography to find the properties of turbulent primary breakup. The results showed that drop properties were related to the properties of the turbulence near the liquid surface and yielded correlations based on phenomenological theories for the onset and end of drop formation along the liquid surface, the evolution of drop size and velocity distributions with distance along the surface and the conditions required for breakup of the liquid column as a whole. It was also found
that aerodynamic effects did not influence the properties of turbulent primary breakup for liquid/gas density ratios greater than 500, providing a substantial data base confirming the negligible role of aerodynamic effects for water/air breakup processes at NTP discussed in connection with Fig.1.
Although the earlier studies of round free turbulent jets have been helpful, a round free turbulent jet where the turbulence decays with increasing streamwise distance is fundamentally different from the attached portion of the turbulent bow sheet illustrated in Fig.1 where the turbulence approximates a stationary wall jet (issues of round as opposed to plane geometry differences aside). Thus, the present investigation was undertaken to consider the properties of transitions for turbulent wall jets and to compare these findings with the earlier findings for turbulent free jets. The present measurements considered the onset conditions for a roughened liquid surface, the location of the onset of turbulent primary breakup along the surface, and the drop sizes produced at the onset of turbulent primary breakup. The experiments involved various liquids injected as wall jets into still air at NTP, with the flows observed using pulsed photography, shadowgraphy and holography. Phenomenological analysis was used to help correlate and interpret the measurements.
EXPERIMENTAL METHODS
Apparatus
The turbulent wall jet apparatus is illustrated in Fig.3. The test liquid was placed within a test chamber that has a round, sharp-edged nozzle at its bottom. Combined with a rod passing down the axis of the test chamber and the nozzle, this configuration provided an initially nonturbulent annular wall jet flow along the rod. Premature liquid outflow was prevented by placing an annular cork in the nozzle exit. The liquid was then forced through the nozzle, ejecting the cork down the rod at the start of the flow, by admitting high-pressure air to the top of the test chamber through a solenoid-actuated
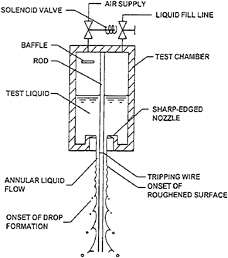
Fig. 3. Sketch of bow-sheet test apparatus.
valve. A baffle near the air inlet to the test chamber reduced mixing between the air and the test liquid. The solenoid was closed at the end of liquid delivery, allowing the test chamber to vent to the ambient pressure. The annular cork was then replaced in the nozzle exit so that the system could be resupplied with liquid through the liquid fill-vent line for the next test.
The high-pressure air was obtained from the laboratory air supply system (dew point<240 K) and stored in an air accumulator at the upstream side of the solenoid valve. The air accumulator had a volume of 0.25 m3 and provided air at pressures up to 1.3 MPa. The test chamber had an inside diameter of 50 mm and a length of 195 mm while the rod diameter was 6.4 mm. Two different nozzle diameters were used to provide annulus heights of 2.3 and 4.3 mm. Injection was vertically downward with the liquid captured in a baffled tub. Instrumentation was mounted rigidly; therefore, various positions in the flow were observed by moving the entire test chamber assembly using vertical and horizontal traversing systems.
Tripping wires were positioned near the exit of the nozzle in order to initiate growth of a turbulent boundary layer along the rod at a well-defined location. The tripping wires had diameters in the range 0.1–0.4 mm and were designed so that k/b< 15%, and with the laminar boundary layer thickness at the location of the tripping wire less than 15% of the annulus thickness, in order to avoid separation of the annular flow from the rod due to the presence of the tripping wire. It was also necessary to provide large enough values of u*k/vf to insure that transition actually occurred at the tripping wire; this issue will be discussed in more detail later.
Total times of injection were 250–1250 ms. These relatively short times were not a problem, however, because flow development times were short for the present wall jets, roughly 10–80 ms. Additionally, measurements were made using pulsed photography, shadowgraphy and holography, which required times less than 100 µs for triggering and data accumulation. Jet velocities were calibrated in terms of the test chamber pressure and liquid type using a short center rod (extending only to the underside of the test chamber) in conjunction with an impact plate.
Instrumentation
Instrumentation consisted of pulsed photography, shadowgraphy and holography, using arrangements and methods similar to (16–25). Pulsed direct photography was used for flow visualization based on a flashlamp (Xenon Corp. Micropulse, Model 457A) depositing 50 mJ in roughly 5 µs. The flow was observed using roughly a 100×125 mm film format at a magnification of 1.1, focused at the median plane of the annular wall jet. These photographs were obtained with an opened camera shutter under darkroom conditions with the flash duration controlling the exposure time.
Pulsed shadowgraph photography was used to measure turbulent primary breakup properties near the onset of breakup as well as the streamwise location of the onset of breakup. The holocamera was used for this purpose with the reference beam blocked to yield a shadowgraph rather than a hologram. The light source was a Spectra Physics GCR-130 pulsed YAG laser, depositing up to 200 mJ of optical energy in roughly 7 ns. This laser beam was expanded to a 46 mm diameter collimated beam for the purpose of flash photography. The shadowgraph image was obtained using the same camera system as the flash photography, with magnifications of 2.0 and 4.5. Data was found by observing the photographs using the same optical arrangement as the hologram construction system. The photographs were mounted on a computer controlled x-y traversing system (having 1 µm resolution) and observed with an MTI Model 65 video camera with optics to provide fields of view of roughly 1.0 ×1.2 mm and 2.5×3.0 mm that could be traversed in the z direction (with 5 µm resolution). The video image was analyzed using Image-Pro Plus software.
Drops and more-or-less ellipsoidal-shaped objects were sized from the shadowgraphs by measuring their maximum and minimum diameters through the centroid of the image. Then assuming that the liquid element was ellipsoidal, its diameter was taken to be the diameter of a sphere having the same volume. This approach is not adequate for elongated objects which were analyzed by measuring the perimeter and cross-sectional area of the image and then defining the size of the object as before, based on an ellipsoid having the same properties.
The holocamera was similar to past work (17–25) except that the YAG laser mentioned earlier was used instead of a ruby laser. An off-axis holographic arrangement was used. The optical penetration properties of the holocamera were improved for use in dense sprays by reducing the diameter of the object beam through the flow and subsequently expanding it (3:1) back to the same size as the reference beam (85 mm) when the two beams were optically mixed to form a hologram. The high power and short duration of the laser pulse allowed the motion
of even small drops to be stopped so that drops as small as 2 µm in diameter could be observed and drops as small as 5 µm in diameter could be measured. The holograms were reconstructed using a 15 mW HeNe laser with the laser beam collimated at a 60 mm diameter and passed through the hologram to provide a real image of the spray in front of the hologram. Analysis of the reconstructed images was the same as the shadowgraphs with x and y traversing of the hologram and z traversing of the video camera.
Experimental uncertainties (95% confidence) of the location of the onset of breakup were less than 30%, similar to past work (21–25), which is relatively large due to the angular variation of ligaments protruding from the surface, the randomness of drop separation from the tips of ligaments and the fact that only one measurement of onset location was made for each test which limited statistics. Measurements of drop properties consisted of the Sauter mean diameter (SMD) by summing over roughly 50 objects at each condition to obtain experimental uncertainties (95% confidence) less than 20%, mainly dominated by sampling limitations.
Test Conditions
Test liquids included water, ethyl alcohol and various glycerol mixtures (21, 42 and 63% glycerol), annulus widths of 2.3 and 4.3 mm, and mean annulus velocities of 15–38 m/s. These conditions yield ranges of experimental parameters, as follows: ρf/ρg= 680–980, ReD=10,000–600,000, WefΛ= 4,000–53,000 and OhD=0.0008–0.0121.
RESULTS AND DISCUSSION
Flow Visualization
Flash photographs of annular wall jet flow, with growth of a turbulent boundary layer initiated by a tripping wire, appear in Fig. 4. This experiment involved water flow with an annulus height of 2.3 mm and mean liquid velocity of 31.1 m/s. The tripping wire can be seen near the top of the left-most photograph, with progressively increasing

Fig. 4. Pulsed photographs of a bow-sheet of water.
distance from the tripping wire proceeding from top to bottom and left-to-right. The capability of the sharp-edged nozzle to generate a turbulence-free initial flow is evident from the smooth surface of the flow prior to reaching the tripping wire. For these conditions, the boundary layer along the wall is laminar prior to reaching the tripping wire as well, with growth of a turbulent boundary layer beginning along the wall at the location of the tripping wire.
Both transitions of interest during the present investigation—onset of a roughened liquid surface and onset of turbulent primary breakup—can be seen in the flash photographs of Fig.4. The surface of the wall jet remains smooth for some distance past the tripping wire. Once surface roughness begins, both the degree of surface roughness and the size of surface roughness elements increase with increasing distance from the tripping wire. The roughness elements become surprisingly long as ligaments protruding from the samples, and eventually begin to form drops by breakup of these tips at the onset of turbulent primary breakup.
It is of interest to compare present visualizations of wall jets with earlier visualizations of round turbulent free jets (13– 15,16–25). First of all, there is no counterpart to the onset of a roughened
surface seen in the present wall jets with a comparable transition in the turbulent free jets. In particular, turbulence penetrates very rapidly to the liquid surface after the exit of the turbulent free jet from the passage and the distance of this transition has not been resolved during previous work (16–25). The process leading to the onset of turbulent primary breakup, however, is rather similar for both flows: the scale of surface distortion and the length of ligaments protruding from the surface both progressively increase, until turbulent primary breakup begins by drop formation at the tips of the ligaments. These similarities will be exploited later to develop correlations for the properties of the onset of turbulent primary breakup for wall jets.
The qualitative behavior of the onset of a roughened liquid surface, the subsequent development of liquid surface distortions, and the properties of the onset of turbulent primary breakup, can be seen rather clearly from pulsed shadowgraph photographs— particularly for the glycerol mixtures. A typical example, for a 62% glycerol mixture with an annulus height of 2.3 mm and a mean liquid velocity of 17.3 m/s, appears in Fig.5. In this case, the tripping wire was located slightly above the top of the left-most shadowgraph, with progressively increasing distance from the tripping wire proceeding from top-to-bottom and left-to-right. Similar to the wall jet illustrated in Fig.4, the initial flow is nonturbulent and the wall boundary layer remains laminar up to the tripping wire, while a turbulent boundary layer begins to develop along the wall beginning at the location of the tripping wire.

Fig. 5. Pulsed shadowgraphs of a bow-sheet of 63% glycerol.
Analogous to the discussion in connection with Fig.2, the shadowgraphs of Fig.5 show that the liquid surface remains smooth for a time as distance increases past the location of the tripping wire. The onset of surface roughness is finally observed, however, toward the bottom of the left-most shadowgraph. Subsequent increases of distance are accompanied by progressively increasing surface roughness and size of roughness elements. The ligaments projecting from the liquid surface become long with increasing distance as well, and eventually break up at their tips, causing the onset of turbulent primary breakup. Further increases of distance into the turbulent primary breakup region yields progressively increasing ligament diameters, ligament lengths, and drop sizes after primary breakup. Taken together, these trends are very similar to past observations of turbulent primary breakup in instances where aerodynamic effects are small (22–25).
Onset of a Roughened Surface
As discussed in connection with Fig. 2 , the onset of surface roughness is thought to occur when the growing boundary layer along the surface attains a thickness comparable to the thickness of the wall jet. This hypothesis will be explored in the following, considering three cases: (1) untripped laminar boundary layer reaches the surface first, (2) untripped laminar boundary layer makes the transition to a turbulent boundary layer which subsequently reaches the surface, and (3) tripped turbulent boundary layer reaches the surface first. Boundary layer development within the wall layer will be simplified considerably for present analysis of this problem, as follows: effects of the free surface on boundary layer growth will be ignored; variation of wall jet mean velocity and thickness will be ignored because values of x/b are modest for both present test conditions and most practical bow sheets (x/b<100); aerodynamic effects will be ignored as discussed earlier, the wall surface will be assumed to be smooth; and liquid properties will be assumed to be constant.
Consider the interaction between the laminar boundary layer and the surface first. Under the present assumptions, the well-known expression for the variation of the thickness of a laminar boundary layer developing along the wall is (4):
δ/x=5.0/Rex1/2 (1)
where x is the streamwise distance from the onset of boundary layer growth and δ represents the distance normal to the wall where the streamwise velocity reaches 99% of ūo. Then, the condition where the outer edge of the laminar boundary layer begins to interact with the surface of the wall jet (although whether this would lead to a roughened surface for a laminar boundary layer is debatable) is given by b=Crδ at x= xr, where Cr is an empirical constant. Then, introducing the hydraulic diameter of the wall jet for present experimental conditions:
D/b=4(1+b/drod) (2)
the expression for xr becomes:
xr/D=(b/(5CrD))2ReD (3)
This untripped laminar regime will continue until the boundary layer becomes turbulent before its outer edge reaches the surface, which will be defined in the following as the condition where Rext=3.2×105, see (4).
Turbulent boundary layer growth must be considered when ![]() The following discussion of this regime is based on Schlichting (4) assuming a 1/7th power law velocity distribution, which is reasonable for the present Reynolds number range, and considering the same definition of boundary layer thickness, δ, as before. Then the expression for the streamwise distance where the turbulent boundary layer begins to interact with the surface becomes:
The following discussion of this regime is based on Schlichting (4) assuming a 1/7th power law velocity distribution, which is reasonable for the present Reynolds number range, and considering the same definition of boundary layer thickness, δ, as before. Then the expression for the streamwise distance where the turbulent boundary layer begins to interact with the surface becomes:
(xr-xt)/D=3.46[(Crb/D)5/4 –(δr/D)5/4]ReD1/4 (4)
where Cr is an empirical constant appropriate for turbulent boundary layer conditions.
The third situation involves a tripped boundary layer at x=0 so that xt=δt=0 in equation (4). As a result, the distance to onset of a roughened liquid surface for a tripped turbulent boundary layer becomes:
xr/D=3.46(Crb/D)5/4ReD1/4 (5)
where Cr is an empirical constant and b/D is given by equation (2).
Experimental evaluation of the ideas expressed by equations (1)–(5) proceeded in two stages, involving consideration of the variation of xr with ReD, and evaluation of the variation of xr with tripping wire properties. The latter considerations showed that the onset of liquid surface roughness due to a turbulent boundary layer along the wall was not significantly affected by tripping wire properties as long as u*k/vf>50 so that the disturbance due to the wire was sufficiently strong. Thus, effects of ReD will be considered first for this strong tripping wire disturbance limit
Present measurements of xr are plotted as suggested by equation (5) in Fig. 6 , considering results for various test liquids over the present range of test conditions. Results shown on the figure include the measurements using the tripped turbulent boundary layer expression of equation (5), and three so-called theoretical results based on equation (3) for an untripped turbulent boundary layer/surface interaction, on equation (4) for an untripped turbulent boundary layer/surface interaction, and on equation (5) for a the tripped turbulent boundary layer/surface interaction. For these “theoretical” results, the plane wall layer approximation has been made, i.e., D/b=4 from equation (2), and C r=1; these selections are not critical because the results that follow are mainly for illustrative purposes.
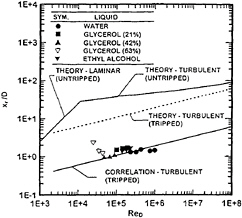
Fig. 6 Influence of Reynolds number on the onset of a roughened surface for bow sheets.
The untripped laminar and turbulent boundary layer predictions meet where Rex= Rext. For the same criteria, the tripped turbulent boundary layer predictions yield generally smaller values of xr/D than the untripped predictions, due to the faster mixing rates of the turbulent boundary layer. Except for low values of ReD, where poorly developed turbulence in the boundary layer probably retards the appearance of a wrinkled liquid surface (24), a correlation based on tripped turbulent boundary layer predictions of equation (5) is seen to provide an excellent fit of the data, as follows:
xr/D=0.061 ReD1/4, ReD>30,000 (6)
where the criterion ReD>30,000 for onset of effects associated with turbulent wall jets is very similar to the analogous criterion found by Wu et al. (24) for turbulent free jets. Based on equation (5), the coefficient obtained from the fit of equation (6) implies Cr=0.2, which is a reasonable value in view of the present rather arbitrary, and conservative, estimate of boundary layer thickness.
The height of the tripping wire influenced the onset of a roughened liquid surface. This effect was correlated in terms of a Reynolds number based on the wire diameter and the friction velocity, where (4):
(7)
and
(8)
where xk denotes the streamwise position of the tripping wire measured from the nozzle.
Present measurements of the effect of tripping wire Reynolds number on xr are plotted in Fig.7. The coordinates of this plot have been selected based on equation (6), where ![]() should be a constant based on the growth of a tripped turbulent boundary layer developing along the wall of the turbulent wall jet; this correlation from equation (6) also is illustrated on the figure.
should be a constant based on the growth of a tripped turbulent boundary layer developing along the wall of the turbulent wall jet; this correlation from equation (6) also is illustrated on the figure.
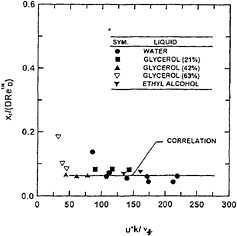
Fig. 7. Influence of tripping wire properties on the onset of a roughened surface for bow sheets.
Aside from a possible outlier for a water wall jet at the lowest tripping wire Reynolds number considered for this liquid, the results show little effect of tripping wire properties for ![]() Below these limits, xr progressively increases with decreasing
Below these limits, xr progressively increases with decreasing
![]() This behavior follows because the tripping wire disturbance is too weak to initiate a fully turbulent wall boundary layer for these conditions. In this weak tripping wire regime, behavior tends toward delayed onset of a roughened liquid surface, analogous to the differences between the untripped and tripped “theoretical” estimates of xr/D illustrated in Fig.6.
This behavior follows because the tripping wire disturbance is too weak to initiate a fully turbulent wall boundary layer for these conditions. In this weak tripping wire regime, behavior tends toward delayed onset of a roughened liquid surface, analogous to the differences between the untripped and tripped “theoretical” estimates of xr/D illustrated in Fig.6.
Onset of Primary Breakup
Approximate analysis to find properties at the onset of turbulent primary breakup was carried out for the turbulent wall jets, using methods analogous to earlier considerations of properties at the onset of turbulent primary breakup for round free turbulent jets (22). This analysis is based on the flow configuration illustrated in Fig.8. The process involves the formation of a drop from a turbulent eddy having a characteristic size, ℓ, and a characteristic cross-stream velocity relative to the surrounding liquid of ![]() The eddy, is shown with a somewhat elongated shape because length scales in the streamwise direction are generally larger than in the cross-stream direction for typical jet-like flows, e.g., values of the ellipticity, ep, up to roughly 2 have been observed for turbulent primary breakup of round free turbulent jets (22). Onset of turbulent primary breakup occurs after the onset of a
The eddy, is shown with a somewhat elongated shape because length scales in the streamwise direction are generally larger than in the cross-stream direction for typical jet-like flows, e.g., values of the ellipticity, ep, up to roughly 2 have been observed for turbulent primary breakup of round free turbulent jets (22). Onset of turbulent primary breakup occurs after the onset of a
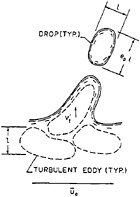
Fig. 8. Sketch of turbulent primary breakup at the liquid surface.
wrinkled liquid surface. This suggested that the wall jet is reasonably turbulent at the onset of turbulent primary breakup so that the turbulence properties of the wall jet can be taken to be the same as a fully-developed turbulent pipe flow for the same hydraulic diameter ReD (5,6). Other assumptions were the same as analysis of the onset of a wrinkled liquid surface: values of the mean velocity and the thickness of the wall jet were assumed to be constant at ūo and b, other physical properties were assumed to be constant, and aerodynamic effects were assumed to be small. Thus, the eddy was assumed to convect in the streamwise direction at the local mean velocity, uo, while the drop formed by the eddy was assumed to have a diameter comparable to ℓ.
Based on both shadowgraph observations and time scale considerations, the drops at the onset of turbulent primary breakup are the smallest drops that can be formed by this mechanism. For turbulence, however, the the smallest drops that can be formed are either comparable to the smallest scale of the turbulence, the Kolmogorov microscale, or to the smallest eddy that has sufficient kinetic energy relative to its immediate surroundings to provide the surface energy needed to form a drop, whichever is larger. For fully-developed turbulent pipe flow, the Kolmogorov length scale can be estimated as follows (26):
(9)
where the streamwise integral length scale has been taken to be equal to 4Λ based on Laufer's measurements for fully-developed turbulent pipe flow (6). For present conditions, values of ℓK are less than 10 µm, which is much smaller than the smallest drop size observed experimentally at the onset of turbulent primary breakup for the present conditions; therefore, only energy requirements will be considered to find drop properties at the onset of turbulent primary breakup in the following.
The energy criterion for the smallest drop that can be formed is found by equating the kinetic energy of an eddy of characteristic
size ℓi, relative to its surroundings, to the surface energy required to form a drop, as follows:
(10)
where only crude proportionality is implied, due to effects of ellipticity, nonuniform velocities within the eddy and the efficiency of the conversion of kinetic energy into surface energy. The largest eddy length scales are comparable to Λ while ℓK<ℓi as just discussed. Then it is reasonable to assume that ℓi is within the inertial range of the turbulence spectrum, where ℓi and vℓi are related as follows (26):
(11)
while variations of turbulence properties within the liquid have been ignored, similar to earlier considerations of turbulent primary breakup for round turbulent free jets (22). Combining equations (10) and (11), setting SMDi ~ ℓi and assuming that turbulence properties within the liquid can be approximated by the properties of fully-developed turbulent pipe flow for a velocity, diameter and Reynolds number of uO, D and ReD, the expression for SMDi becomes:
(12)
where Csi is an empirical constant involving the various proportionality constants. For fully-developed turbulent pipe flow, ![]() is a constant (5,6); therefore, SMDi/Λ should only be a function of WefΛ for present test conditions. Finally, analogous to the earlier studies of turbulent primary breakup for round turbulent free jets (22,23), the radial integral length scale was taken to be D/8, based on the measurements of Laufer for fully-developed turbulent pipe flow (6).
is a constant (5,6); therefore, SMDi/Λ should only be a function of WefΛ for present test conditions. Finally, analogous to the earlier studies of turbulent primary breakup for round turbulent free jets (22,23), the radial integral length scale was taken to be D/8, based on the measurements of Laufer for fully-developed turbulent pipe flow (6).
The present measurements for SMDi for turbulent wall jets are plotted in terms or the variables of equation (12) in Fig.9, along with the earlier correlation found by Wu et al. (22) for round turbulent free jets. The
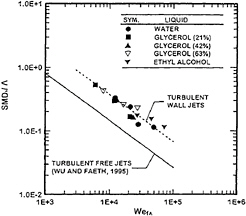
Fig. 9. SMD at the onset of turbulent primary breakup as a function of bow sheet Weber number.
correlation of the present measurements in these coordinates is similar to the earlier free jet result and is well within the scatter anticipated based on experimental uncertainties. The power of WefΛ for the correlation of present measurements is not -3/5, as suggested by equation (12); instead, the power was not statistically different from the earlier round jet results. Thus, the present correlation of SMDi for the turbulent wall jets adopts the same power as the round turbulent free jets, yielding the following empirical fit that is shown on the plot:
(13)
The standard deviations of the coefficient and power of equation (13) are 10 and 8%, respectively, while the correlation coefficient of the fit is 0.96; these parameters are similar the round jet results (22). The reduction of the power from –3/5 in equation (12) to –0.74 in equation (13) is statistically significant but is not large in view of the crude approximations of the present phenomenological analysis. The coefficient of equation (13) is relatively large but this can be anticipated from equation (12) because ![]() is relatively large; thus, Csi is of order unity as anticipated for an empirical
is relatively large; thus, Csi is of order unity as anticipated for an empirical
parameter of this type. The present correlation for turbulent wall jets gives values of SMDi that are somewhat larger than the earlier results for turbulent free jets at the same value of WefΛ, e.g., the constants on the right-hand sides (RHS) of the two correlations are 340 and 133, respectively. This difference is not large in view of the crudeness of the present analysis. In particular, differences of this magnitude might be anticipated when concepts of hydraulic diameter are used to estimate the integral scales of turbulence and to compare findings for turbulent round free jets and wall jets.
Similar to past studies of turbulent round free jets (22,23), it is assumed that the eddy initially forming drops at the onset of turbulent primary breakup convects along the liquid surface with a streamwise velocity uo for the time τi required for an eddy having characteristic size ℓi to form a drop. There are several characteristic breakup times that can be used to estimate τi, discussed by Wu and coworkers (22,23); based on these considerations, the Rayleigh breakup time was chosen for the present analysis. Thus ignoring effects of liquid viscosity on the Rayleigh breakup time, discussed by Weber (27), the expression for τi becomes (22):
(14)
which is independent of vℓi. The distance required for the onset of turbulent primary breakup is then obtained relative to the first appearance of significant effects of turbulence at the liquid surface, as follows:
xi–xr ~ ūoτi (15)
An expression for xi–xr is subsequently found by substituting equation (14) into equation (15) and letting SMDi ~ ℓi, as before:
(16)
Finally, eliminating SMDi from equation (16), using equation (12), yields the following expression for the location of the onset of turbulent primary breakup for wall jets:
(17)
where Cxi is a constant of proportionality and ![]() is a constant for a fully-developed turbulent wall jets.
is a constant for a fully-developed turbulent wall jets.
Present measurements of xi–xr are plotted in terms of the variables of equation (17) in Fig.10, along with the earlier correlation for xi/Λ found by Wu et al. (22)
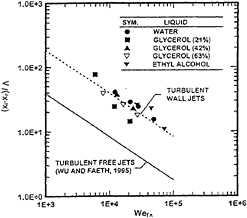
Fig. 10. Length to initiate turbulent primary breakup as a function of bow sheet Weber number.
for round turbulent free jets. The correlation of the present measurements in these coordinates is similar to the earlier free jet results and is well within the scatter anticipated based on experimental uncertainties. As before, however, the power of WefΛ for the present data correlation is not -0.4, as suggested by equation (17), but can be represented better by the following empirical fit that is shown on the plot:
(18)
where the present power of WefΛ was not statistically different from the findings for round turbulent free jets and has been taken to be the same to simplify comparisons
between turbulent round free and wall jet results. The standard deviations of the coefficient and power of equation (18) are 12 and 14%, respectively, and the correlation coefficient of the fit is 0.92. The large value of the coefficient on the RHS of equation (18) can be anticipated from equation (12) because ![]() is quite large for typical turbulent pipe or channel flow. The correlation for the turbulent wall jets is above the correlation for the round turbulent free jets, which is consistent with the relative positions of the SMDi for these two flows seen in Fig.9, and the fact that larger distances to the onset of breakup are required when drop sizes at the onset of breakup becomes large. Finally, the differences between the constants on the RHS of correlations for turbulent wall jets and for round turbulent free jets, 18,800 and 3980, respectively, are reasonable in view of the limitations of estimates of scales from hydraulic diameters, as discussed earlier.
is quite large for typical turbulent pipe or channel flow. The correlation for the turbulent wall jets is above the correlation for the round turbulent free jets, which is consistent with the relative positions of the SMDi for these two flows seen in Fig.9, and the fact that larger distances to the onset of breakup are required when drop sizes at the onset of breakup becomes large. Finally, the differences between the constants on the RHS of correlations for turbulent wall jets and for round turbulent free jets, 18,800 and 3980, respectively, are reasonable in view of the limitations of estimates of scales from hydraulic diameters, as discussed earlier.
CONCLUSIONS
Properties of transitions for the onset of roughened liquid surfaces and turbulent primary breakup for turbulent bow sheets were studied for liquid wall jets in still air at normal temperature and pressure. Experimental conditions involved water, ethyl alcohol and various glycerol mixtures as test liquids, with ρf/ρg=680–980, RefD= 10,000–600,000, WefΛ=4,000–53,000 and OhD=0.008–0.0121. The major conclusions of the study are as follows:
-
Roughness of the liquid surface, and primary breakup into drops along the liquid surface were caused by turbulence due to liquid motion past the wall surface, while direct effects of aerodynamic forces at the liquid surface were small, for present conditions
-
Transition to a roughened liquid surface occurred when the developing turbulent boundary layer along the wall surface reached a thickness that was comparable to the thickness of the wall jet itself. For present conditions, where turbulent boundary layer growth was initiated by a trip wire, distances to the onset of a roughened liquid surface could be correlated based on a turbulent boundary layer thickness expression, see equation (6).
-
Drop sizes at the onset of turbulent primary breakup along the liquid surface could be correlated by equating the surface energy required to form a drop to the kinetic energy of an eddy of corresponding size within the inertial region of the turbulence spectrum, see equation (13). This finding highlights the close correspondence between liquid turbulence properties and turbulent primary breakup properties for turbulent wall jets in still gases, yielding behavior that is similar to turbulent primary breakup of round turbulent free jets in still gases (19,20).
-
The onset of turbulent primary breakup occurs at some distance from the point of onset of liquid surface roughness, but tends to approach this position at WefΛ increases. The distance required for the onset of turbulent primary breakup along the surface could be correlated by considering the distance convected at the mean velocity of the wall jet for the residence time needed to initiate the Rayleigh breakup of ligaments protruding from the liquid surface that are associated with onset-sized drops, see equation (18).
Present results are limited to moderate Ohnesorge number conditions, where the SMD at the onset of turbulent primary breakup corresponds to eddy sizes in the inertial range of the turbulence, and where the relative velocities between the liquid and gas are comparable to the relative velocities between the liquid and the wall surface. Consideration of the Rayleigh breakup of ligaments protruding from the liquid surface, and past findings for round turbulent free jets (18–22), suggest potential effects of liquid viscosity at larger Ohnesorge numbers, difficulties with the present description of turbulent primary breakup as the limits of the inertial turbulent subrange are approached,
and potential aerodynamic effects due to enhancement of ligament motion and merging of turbulent primary and secondary breakup when ρf/ρg<500. Until these effects are better understood, the correlations reported here should not be used outside the present test range. In addition, the streamwise evolution of drop sizes and velocities produced by turbulent primary breakup, and the rate of liquid removal from the wall jet due to turbulent primary breakup, are issues that merit attention in the future.
ACKNOWLEDGMENTS
This research was sponsored by the Office of Naval Research Grant No. N00014–95–1–0234 under the technical management of E.P.Rood. Initial development of research facilities for this study was carried out under Air Force Office of Scientific Research Grant Nos. AFOSR F49620 –92-J-0399 and F49620–95–1–0364 under the technical management of J.M. Tishkoff.
REFERENCES
1. Gad-el-Hak, M., “Measurements of Turbulence and Wave Statistics in Wind-Waves,” International Symposium on Hydrodynamics in Ocean Engineering, The Norwegian Institute of Technology, Olso, Norway, 1981, pp. 403–417.
2. Townson, J.M., Free-Surface Hydraulics, 1st ed., Unwin Hyman, London, 1988, Chapt. 6.
3. Ervine, D.A., and Falvey, H.T., “Behavior of Turbulent Water Jets in the Atmosphere and in Plunge Pools,” Proc. Inst. Civ. Eng., Pt. 2, Vol. 83, Mar. 1987, pp. 295–314.
4. Smith, R.M., and Wang, C.-T., “Contracting Cones Giving Uniform Throat Speeds,” Journal of Aeronautical Sciences, Vol. 11, 1944, pp. 356–360.
5. Schlichting, H., Boundary Layer Theory, 7th ed., McGraw-Hill, New York, 1979, p. 599.
6. Hinze, J.O., Turbulence, 2nd ed., McGraw-Hill, New York, 1975, p. 427 and pp. 724–742.
7. De Juhasz, K.J., Zahm, O.F., Jr., and Schweitzer, P.H., “On the Formation and Dispersion of Oil Sprays,” Bulletin No. 40, Engineering Experiment Station, Pennsylvania State University, University Park, PA, 1932, pp. 63–68.
8. Lee, D.W., and Spencer, R.C., “Preliminary Photomicrographic Studies of Fuel Sprays,” NACA Technical Note 424, Washington, D.C., 1933.
9. Lee, D.W., and Spencer, R.C., “Photomicrographic Studies of Fuel Sprays,” NACA Tech. Note 454, Washington, D.C., 1933.
10. Grant, R.P., and Middleman, S., “Newtonian Jet Stability,” AIChE Journal, Vol. 12, No. 4, 1966, pp. 669–678.
11. Phinney, R.E., “The Breakup of a Turbulent Jet in a Gaseous Atmosphere,” Journal of Fluid Mechanics, Vol. 60, Pt. 4, 1973, pp. 689–701.
12. McCarthy, M.J., and Malloy, N.A., “Review of Stability of Liquid Jets and the Influence of Nozzle Design, ” Chemical Engineering Journal, Vol. 7, No. 1, 1974, pp. 1–20.
13. Hoyt, J.W., and Taylor, J.J., “Waves on Water Jets,” Journal of Fluid Mechanics, Vol. 88, Pt. 1, 1977, pp. 119– 123.
14. Hoyt, J.W., and Taylor, J.J., “Turbulence Structure in a Water Jet Discharging in Air,” Physics of Fluids, Vol. 20, Pt. II, No. 10, 1977, pp. S253–S257.
15. Hoyt, J.W., and Taylor, J.J., “Effect of Nozzle Boundary Layer on Water Jets Discharging in Air, ” Jets and Cavities (J.H. Kim, O.Furuya and B.R.Parkin, ed.) ASME-FED, Vol. 31, American Society of Mechanical Engineers, New York, 1985, pp. 93–100.
16. Ruff, G.A., Sagar, A.D., and Faeth, G.M., “Structure of the Near-Injector Region of Pressure-Atomized Sprays, ” AIAA Journal, Vol. 27, No. 7, 1989, pp. 901–908.
17. Ruff, G.A., Bernal, L.P., and Faeth, G.M., “Structure of the Near-Injector Region of Non-Evaporating Pressure-Atomized Sprays,” Journal of Propulsion and Power, Vol. 7, No. 2, 1991, pp. 221–230.
18. Ruff, G.A., Wu, P.-K., Bernal, L. P., and Faeth, G.M., “Continuous- and Dispersed-Phase Structure of Dense Non-Evaporating Pressure-Atomized Sprays,” Journal of Propulsion and Power, Vol. 8, No. 2, 1992, pp. 280–289.
19. Tseng, L.-K., Ruff, G.A., and Faeth, G.M., “Effects of Gas Density on the Structure of Liquid Jets in Still Gases, ” AIAA Journal, Vol. 30, No. 6, 1992, pp. 1537–1544.
20. Tseng, L.-K., Wu, P.-K., and Faeth, G.M., “Dispersed-Phase Structure of Pressure-Atomized Sprays at Various Gas Densities,” Journal of Propulsion and Power, Vol. 8, No. 6, 1992, pp. 1157–1166.
21. Wu, P.-K., Ruff, G.A., and Faeth, G.M., “Primary Breakup in Liquid/Gas Mixing Layers for Turbulent Liquids, ” Atomization and Sprays, Vol. 1, No. 4, 1991, pp. 421–440.
22. Wu, P.-K., Tseng, L.-K., and Faeth, G.M., “Primary Breakup in Gas/Liquid Mixing Layers for Turbulent Liquids, ” Atomization and Sprays, Vol. 2, No. 3 1992, pp. 295–317.
23. Wu, P.-K., and Faeth, G.M., “Aerodynamic Effects in Primary Breakup of Turbulent Liquids,” Atomization and Sprays, Vol. 3, No. 3, 1993, pp. 265–289.
24. Wu, P.-K., Miranda, R.F., and Faeth, G.M., “Effects of Initial Flow Conditions on Primary Breakup of Nonturbulent and Turbulent Round Liquid Jets,” Atomization and Sprays, Vol. 5, No. 2, 1995, pp. 175–196.
25. Wu, P.-K., and Faeth, G.M., “Onset and End of Drop Formation Along the Surface of Turbulent Liquid Jets in Still Gases,” Physics of Fluids A, Vol. 7, No. 11, 1995, pp. 2915–2917.
26. Tennekes, H., and Lumley, J.L., A First Course in Turbulence, MIT Press, Cambridge, MA, 1972 , pp. 248–286.
27. Weber, C., “Zum Zerfall eines Flussigkeitsstrahles,” Z. Angewesen. Math. Mech., Vol. 2, 1931, pp. 136–141.
DISCUSSION
D.Liepmann
University of California at Berkeley, USA
-
The results shown in Figure 9 and 10 and discussed in the text of the article indicate that both spray generation and initiation length for both turbulent free jets and turbulent wall jets have the same dependence on the Weber Number with just the constant of proportionality differing between the two cases. What is the physical significance of this? Does this imply that in your experiments the presence of a boundary layer has little fundamental effect on the spray dynamics?
-
In the analysis linking turbulent eddy size to droplet generation, an implicit assumption was made that the flow is homogeneous and isotropic. In our experiments at Berkeley (at much lower Reynolds numbers) we find that the droplet size is strongly influenced by instabilities that develop due to the flow geometry. In your paper there is some indication that “the roughness elements become surprisingly long as ligaments protruding from the samples.” Do you see any indication of this comparing droplet sizes from experiments with different sizes or locations of trip wires or, possibly, between the two geometries?
-
In the paper empirical models are presented for droplet generation at extremely high Reynolds Number, which are reasonable for full scale ships. What do the authors think are the next steps needed to (a) understand the fundamental physics of the flow and (b) provide input to numerical simulations or numerical design tools?
AUTHORS' REPLY
Our replies are numbered to correspond to Professor Liepmann's discussion:
-
The presence of a developing turbulent boundary layer along the surface of the wall jets is fundamentally important because the surface only becomes roughened (which is a prerequisite for turbulent primary breakup) when the outer edge of this boundary layer reaches the surface. Beyond this, however, properties at the onset of turbulent primary drop breakup are similar for both free and wall jets because they only depend on properties of turbulence spectra that are the same for both flows. Greater differences between the two flows are possible for the variation of drop properties after turbulent primary drop breakup as a function of distance along the surface but this remains to be seen.
-
The only assumptions made about the properties of the turbulence were that breakup was caused by eddies in the inertial range of the spectrum and that eddy sizes and velocities are related by equation (11); this does not entail an implicit assumption of homogeneous and isotropic turbulence. Without considering the details of Professor Liepmann's experiments, it is difficult to comment about his observations of drops sizes after primary breakup except to note that smaller inertial ranges of the turbulence spectrum at low Reynolds numbers would make large-scale features more important and that initial disturbances of wall jets can dominate the turbulent wall boundary layer phenomena emphasized during the present paper for some experimental configurations. Finally, effects of trip wire and flow properties on drop sizes for the present experiments were explained reasonably well by the phenomenological theories discussed here.
-
There are a number of issues that should be better understood in order to provide the technology base needed to address these flows, including the evolution of drop size/velocity distributions and the rate of production of dispersed liquid due to turbulent primary breakup as a function of distance along the surface. The mean and turbulent structure of the liquid wall jet, the drag and ligament properties at the gas/liquid interface and the structure of the dispersed multiphase flow region adjacent to the liquid wall jet, among others.
















