Hydrodynamic Forces on a Surface-Piercing Plate in Steady Maneuvering Motion
Z.-J.Zou (Wuhan Transportation University, China)
ABSTRACT
This paper describes a three dimensional numerical method for calculating the hydrodynamic forces acting on a surface-piercing vertical plate of small aspect ratio in steady maneuvering motion. Under the potential flow assumption and using a nonlinear vortex model, the disturbance velocity potential is represented by a Rankine source distribution on the free surface and a Rankine-type vortex distribution on the plate and on the vortex sheet in the wake. The vortex and source strengths are determined by satisfying the boundary conditions on the plate and on the free surface, whereas the Kutta condition at the trailing edge and the radiation condition at large distance from the plate are satisfied explicitly.
The proposed method is applied to flat plates of T/L=0.1 and 0.2 in oblique motion and turning motion up to moderate and large drift angle and yaw rate. Numerical results are compared with available experimental results which shows satisfying agreements.
NOMENCLATURE
|
ρ |
fluid density |
|
σ |
source strength |
|
|
disturbance velocity potential |
|
Φ |
disturbance velocity potential in double-body flow |
|
φ |
disturbance velocity potential due to free-surface effects |
1.
INTRODUCTION
For theoretical prediction of the hydrodynamic forces acting on a maneuvering ship, the ship's hull may be considered to be a lifting body of very small aspect ratio. Although a free surface is present, it may be replaced by a rigid horizontal plane in the range of low speeds. In such a case, the effective aspect ratio of the hull is twice its draft-to-length ratio, and the flow is equivalent to the so-called double-body flow to which various theoretical methods developed in aerodynamics may be applied directly. On the other hand, for ships at higher speeds, the free-surface displacement may have a significant influence on the hydrodynamic forces, thus the free-surface effects must be included in the theoretical analysis.
Since the maneuvering behavior of a ship is mainly determined by its lateral underwater profile, a vertical flat plate with the same draft and length may be a useful model for calculating the hydrodynamic forces acting on the ship. For a surface-piercing plate in maneuvering motion, a successful numerical method was proposed by Chapman (1), (2) under the slender-body assumption. Since the flow separation along the lower edge is neglected in this method, its applicability is confined to small lateral motions, and although the aspect ratio is assumed to be small, better agreements between numerical and experimental results were obtained for plates of larger aspect ratios.
Another important fact is that the wake influence is fully neglected in the slender-body theory. As we known, the aspect ratio is an important measure of the effects of three dimensionality and the trailing wake is an inevitable consequence of these effects. In the case of very large aspect ratio, the flow around a vertical plate may be viewed as two dimensional in the horizontal plane, whereas in the limiting case of zero aspect ratio the flow is essentially two dimensional cross flow in the lateral plane. On the other hand, for a plate with small but finite aspect ratio, three dimensional flow effects may be important, and the influence of trailing wake must be taken into account.
For a yawed surface-piercing flat plate, Maniar et al. (3) proposed a three-dimensional panel method using Kelvin singularities. In correspondence with the conventional linear lifting-surface theory, the normal dipole distribution on the plate and in the wake downstream of the trailing edge is put on the plane of the plate. Thus this method, just as Chapman's method, is only applicable to a plate of moderate or larger aspect ratio at small drift angle.
Recently, for a surface-piercing plate in steady turning motion, Landrini and Campana (4) presented a three dimensional numerical method using Rankine singularities. The Neumann-Kelvin boundary-value problem was solved by coupling a standard panel method on the free surface with a vortex lattice procedure on the body and wake surface, where corresponding to the nonlinear lifting-surface theory a nonlinear wake modeling was used.
In the present paper, a three-dimensional Rankine panel method for free-surface flow around a vertical plate of small aspect ratio in steady oblique motion and/or turning motion is presented. The flow is assumed to separate from the trailing edge and the lower edge. The wake is modeled by a nonlinear vortex sheet. The boundary condition on the free surface is linearized with respect to the double-body flow. To solve the linearized boundary-value problem, a source distribution on the free surface and a vortex distribution on the plate and in the wake are used, whereas the singularity strengths are determined by satisfying the corresponding boundary conditions.
Calculations were performed for rectangular flat plates of draft-to-length ratio 0.1 and 0.2. Numerical results were presented and compared with other theoretical, numerical and experimental results where available.
2.
MATHEMATICAL FORMULATION
We consider a vertical rectangular plate in steady maneuvering motion at the plane of the undisturbed free surface. The geometric aspect ratio, the draft-to-length ratio T/L, is assumed to be small.
We adopt a right-handed Cartesian coordinate system o-xyz which is fixed with respect to the moving plate, see Fig.1. The translation velocity of the plate in the horizontal plane is ![]() and the yaw rate about the vertical axis is r. The velocity components in the longitudinal and lateral directions are u=V0 cos β and v=–V0 sin β, respectively, where β is the drift angle and
and the yaw rate about the vertical axis is r. The velocity components in the longitudinal and lateral directions are u=V0 cos β and v=–V0 sin β, respectively, where β is the drift angle and ![]() .
.
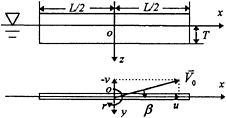
Fig. 1 Coordinate system
The fluid is assumed to be inviscid and imcompressible. The flow is assumed to be irrotational except in the wake which is to be modeled by a trailing vortex sheet. The disturbance velocity of the fluid can be expressed by the gradient of a velocity potential ![]() which satisfies the Laplace equation
which satisfies the Laplace equation
![]() 2
2![]() =0 (1)
=0 (1)
in the fluid domain and some boundary conditions.
On the plate which is located on the plane y=0, the boundary condition is given by
![]() y=v+rx (2)
y=v+rx (2)
On the free surface z=ζ(x,y) the velocity potential should satisfy a kinematic boundary condition and a dynamic boundary condition:
(3)
(4)
where ζ is the free-surface elevation, g is the gravitational acceleration and
Together with the boundary conditions on the free surface, a radiation condition must be imposed to ensure that there are no waves radiated upstream.
Moreover, the disturbance created by the motion of the plate should decay to zero at infinity:
(5)
where ![]()
The kinematic and dynamic boundary conditions (3) and (4) are combined to give a single boundary condition on the free surface:
(6)
This boundary condition is nonlinear and should be imposed on the exact free surface z=ζ which is not known in advance. To solve the boundary-value problem for the velocity potential ![]() , we decompose
, we decompose ![]() into a velocity potential for the double-body flow, Φ, and another one due to the free-surface effects, φ.
into a velocity potential for the double-body flow, Φ, and another one due to the free-surface effects, φ.
Assuming that ![]() on the undisturbed free surface z=0, we linearize the boundary conditions on the free surface about the double-body flow at z=0 in correspondence with Dawson's method (5).
on the undisturbed free surface z=0, we linearize the boundary conditions on the free surface about the double-body flow at z=0 in correspondence with Dawson's method (5).
Since Φz=0 and Φxz=Φyz=0 on z=0, it follows from (4) that
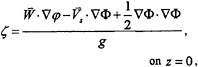
(7)
where ![]()
Similarly, since Φxxz=Φxyz=Φyyz=0 on z=0, we obtain from (6)
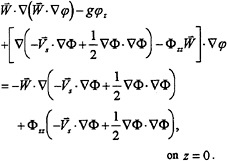
(8)
Correspondingly, the boundary condition (2) on the plate can be rewritten as
φy=–[Φy–(v+rx)]
Once the double-body flow is known, the linearized boundary-value problem for the velocity potential φ can be solved by distributing singularity elements with unknown strengths over the boundary surfaces. Considering a surface-piercing plate of zero thickness, we represent the flow around the plate by a Rankine source distribution on the free surface surrounding the plate and a Rankine-type vortex distribution on the plate and in the wake.
Corresponding to the vortex distribution, a Kutta condition should be imposed at the trailing edge (T.E.) to determine the circulation. This condition can be satisfied by requiring that the vortex strength along the trailing edge is zero, i.e.
γT.E.=0
Moreover, a dynamic boundary condition should be imposed on the trailing vortex sheet which states that there is no pressure difference across the vortex sheet in the wake. In principle, an iterative procedure is required to satisfy this condition, since the location of the trailing vortex sheet is not known in advance. However, for practical applications in engineering problem it is usually sufficient to assume the shape and location of the trailing vortex sheet in advance.
For a plate of small aspect ratio the flow may separate from the lower edge along the length even if the drift angle or yaw rate is small. Therefore, a nonlinear trailing vortex model is required. In the present paper, we use a nonlinear vortex model which is an extension of Bollay's nonlinear theory (6). It is assumed that the trailing vortices separate from the plate at the trailing edge and lower edge at some angle to the plane of the plate and extend to infinity downstream in some prescribed manner. The vertical plate is divided horizontally into lifting strips. On each lifting strip the vortex strength changes only in the longitudinal direction, whereas from one lifting strip to another the vortex strength changes its value in the vertical direction. For a plate of extremely small aspect ratio, one lifting strip is sufficient, and the proposed vortex model is consistent with Bollay's model. On the other hand, for a plate at extremely small drift angle or yaw rate the trailing vortices may be put on the plane of the plate, then the vortex model corresponds to the conventional linear lifting-surface theory.
With the shape and location of the trailing vortex sheet assumed in advance, the source and vortex
strengths can be determined by satisfying the boundary conditions on the free surface and on the plate. Then we can calculate the free-surface elevation by (7) and the hydrodynamic forces on the plate by integrating the fluid pressure over the plate.
In the body-fixed coordinate system the dynamic pressure in the fluid relative to the atmospheric pressure is given by
where ρ is the fluid density.
Since on the plate y=0 and
where the superscripts + and – denote the right and left sides of the plate, y=+0 and y=–0, respectively, the jump of dynamic pressure across the plate is
or with the relation ![]() where γ is the bound vortex strength, the vertical component of the vortex strength vector,
where γ is the bound vortex strength, the vertical component of the vortex strength vector,
p+–p–=–ρuγ (10)
Corresponding to the decomposition of ϕ, γ can be devided into a part in the double-body flow and a part due to the free-surface effects:
γ=γ0+γ1,
where,
![]()
Consequently, the lateral force and yaw moment acting on the plate are given by
(11)
(12)
which can be expressed in nondimensional form as
3.
NUMERICAL SOLUTION
A three-dimensional panel method is applied to solve the potential flow problem. In order to construct the numerical solution, the boundary surfaces and the singularity distributions are discretized.
The plate is discretized into panels. On each of the panels, a collocation point is selected to satisfy the boundary condition on the plate. Correspondingly, the vortex distribution on the plate and on the trailing vortex sheet is discretized and replaced by concentrated vortex elements. As conventional, the vortex strength vector is decomposed into a vertical component (bound vortex) and a horizontal component (free vortex). For steady flow considered here, it follows from the dynamic boundary condition on the trailing vortex sheet that the vertical component of the vortex strength vector is zero in the wake.
On the plate, the longitudinal and vertical locations of the line vortices and the collocation points are determined in a similar way as by the well-known quasi-continuous method (QCM), Lan (7). Assuming that on the plate there are NL panels and NZ panels in the longitudinal and vertical directions respectively, then for i=1,2,…, NL, and j=1,2,…, NZ the locations of the line vortices are given by
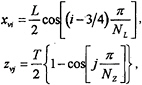
and the locations of the collocation points by
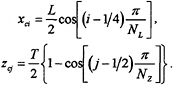
The line vortices separate from the plate at the trailing and lower edges and extend to infinity downstream, thus form a discrete vortex system with NP=NL×NZ unknown vortex strengths γk, k=1,2,…,Np.
Neglecting the free-surface effects, the vortex strengths γok corresponding to the double-body flow can be determined by satisfying the boundary condition on the plate, Φy=v+rx, at the collocation points (xci,0,zcj).
For the free-surface flow, besides the discretization of the plate and the vortex distribution the undisturbed free surface is discretized into quadrilateral panels whose langth is approximately constant. On each of these panels, a source distribution with constant strength is covered, and the “middle point” is selected as collocation point at which the boundary condition on the free surface is satisfied. Assuming that there are NF panels on the free surface, the source strength σj (j=1,2,…, NF) and the vortex strength γ1k (k=1,2,…,NP) are determined simultaneously by satisfying the boundary conditions (8) and (9) at the collocation points on the free surface and on the plate. On the other hand, the radiation condition is satisfied explicitly by the numerical technique of “staggered grids”, see e.g. Jensen et al. (8), where the source panels on the undisturbed free surface are shifted backwards by one panel length relative to the corresponding free surface panels.
4.
NUMERICAL RESULTS
The proposed numerical method was applied to flat plates of T/L=0.1 and 0.2 in oblique motion and in turning motion.
For a plate in oblique motion the local drift angle is constant and equal to the drift angle of the plate. Similarly to Bollay's vortex model we assume that the free vortices are straight line vortices which separate from the trailing edge and lower edge at an angle equal to half of the drift angle and extend to infinity downstream.
In order to verify the proposed method, calculations were first performed for a plate of T/L=0.1 in oblique motion in double-body flow. The corresponding effective aspect ratio is λe=0.2.
Fig.2 shows the numerical results obtained by the present method together with experimental results by Flachsbart, see (6), and theoretical results. The numerical results are obtained with NL×NZ=20×10 panels on the plate. The “theoretical” results are obtained by the following formula, see e.g. Thieme ( 9):
(13)
(14)
where r′=r L/u is the nondimensional yaw rate, and r′=0 in the present case.
As shown in Fig.2, the present results agree quite well with both the experimental and theoretical results. The nonlinear dependence of the lateral force on the drift angle is predicted very well by the present method.
The proposed method was then applied to surface-piercing plates. Fig.3 shows the numerical results for a plate of T/L=0.1 in oblique motion at Fn=0.30. The free-surface grid reaches about 0.25L upstream and 1.5L downstream of the plate, and 1.0L laterally. The panel length is about 0.05L which corresponds to approximately 12 panels per wave length. In Fig.3 numerical results obtained for the
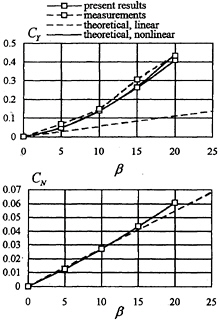
Fig. 2 Lateral-force and yaw-moment coefficients for a plate of λe=0.2 in oblique motion in double-body flow
plate in double-body flow are also shown for comparison. It can be seen that in this case the free-surface effects on the hydrodynamic forces can be neglected.
Fig.4 shows the calculated hydrodynamic coefficients versus nondimensional sway speed v′=–tan β for a plate of T/L=0.2 in double-body flow and in free-surface flow at Fn=0.32. The discretization of the plate and the free surface is the same as in the case of the plate of T/L=0.1. In Fig.4, the numerical results are compared with measurements by van den Brug et al. (10). Regarding the yaw-moment, the agreement of the numerical results with measurements is quite satisfactory. On the other hand, although the nonlinear dependence of the lateral force on drift angle is predicted by the present method, quantitatively, there is a discrepancy between
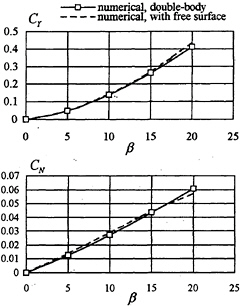
Fig.3 Lateral-force and yaw-moment coefficients for a plate of T/L=0.1 in oblique motion at Fn=0.30
the numerical results and measurements, especially at large drift angle. In addition, comparison between the numerical results obtained for double-body flow and free-surface flow shows that also in this case the free-surface effects are not significant.
For a plate in steady turning motion, the local drift angle at point (x,y,z) is given by
We assume that the free vortices leave the plate at the trailing and lower edges at an angle equal to half of the local drift angle and travel downstream along curved routes. The free vortices are discretized into straight vortex segments, the length of which is approximately equal to the length of free-surface
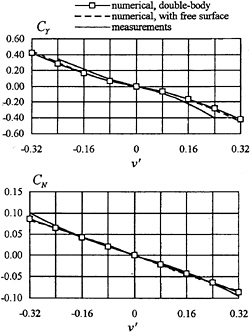
Fig.4 Comparison of the lateral-force and yaw-moment coefficients for a plate of T/L=0.2 in oblique motion at Fn=0.32
panels. Starting from the trailing edge or the lower edge, the free vortices in their ![]() discrete form go backwards at an angle equal to . At large distance from the plate, the free vortices are replaced by straight line vortices which extend to infinity downstream.
discrete form go backwards at an angle equal to . At large distance from the plate, the free vortices are replaced by straight line vortices which extend to infinity downstream.
Calculations were performed for surface-piercing plates of T/L=0.1 and 0.2 in steady turning motion at Fn=0.3 and 0.32, respectively.
The sizes of the free surface grid and free surface panels are approximately equal to those used for the plate in oblique motion, whereas the discretization of the plate is exactly the same.
In Fig.5 the calculated lateral-force and yaw-moment coefficients versus nondimensional yaw rate
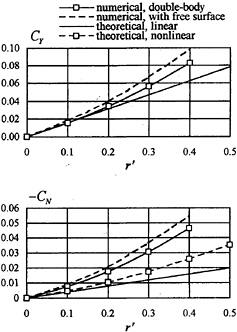
Fig. 5 Lateral-force and yaw-moment coefficients for a plate of T/L=0.1 in turning motion at Fn=0.30
r′ is shown together with theoretical results obtained by (13) and (14) for the plate of T/L=0.1 at Fn=0.30. In contrast to the theoretical prediction, the present results show a strong nonlinear dependence of the hydrodynamic force and moment on the yaw rate, especially for the yaw-moment. Moreover, comparison between the numerical results obtained for the plate in double-body flow and in free-surface flow indicates that the free-surface effects tend to increase the hydrodynamic force and moment, especially at large yaw rate, and thus should not be ignored in these cases.
Fig.6 shows the calculated lateral-force and yaw-moment coefficients for the plate of T/L=0.2 in turning motion at Fn=0.32 in double-body flow and in free-surface flow. It can be seen that the free
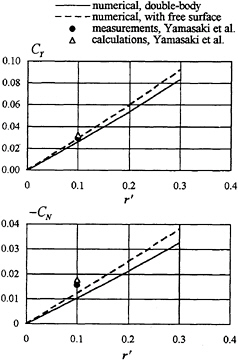
Fig. 6 Comparison of the lateral-force and yaw-moment coefficients for a plate of T/L=0.2 in turning motion at Fn=0.32
surface effects are remarkable in this case. In Fig.6 the measurements and numerical results by Yamasaki et al. (11) are also plotted for comparison, where the numerical results are obtained by an approach similar to Chapman's method. The lateral force calculated by the present method is in very good agreement with the measurement, whereas the yaw moment is underestimated by the present method in comparison with the measurement.
5.
CONCLUSIONS
A three-dimensional panel method using Rankine singularities and a nonlinear vortex model is developed for calculating the hydrodynamic forces acting on a vertical surface-piercing plate of small aspect ratio in steady oblique motion and turning motion. The numerical results are compared with other theoretical, numerical and experimental results which are available. It is shown that the present method can predict very well the free-surface effects on the hydrodynamic forces and the nonlinear dependence of the hydrodynamic forces on the drift angle and yaw rate.
For applications in ship maneuvering problem, the proposed method is to be extended to bodies including the effect of thickness.
ACKNOWLEDGEMENTS
The computations were performed at the Computer Center of Hamburg University during the author's stay in Hamburg. The author is grateful to Prof. Soeding for valuable discussions.
REFERENCES
1. Chapman, R.B., “Free-Surface Effects for Yawed Surface-Piercing Plates”, Journal of Ship Research, Vol. 20, No.3, 1976, pp. 125–136.
2. Chapman, R.B., “Prediction of Free-Surface Effects on Ship Manoeuvring”, Proceedings of the 11th Symposium on Naval Hydrodynamics, London, England, 1976, pp.533–543.
3. Maniar, H., Newman, J.N., and Xu, H., “Free-Surface Effects on a Yawed Surface-Piercing Plate”, Proceedings of the 18th Symposium on Naval Hydrodynamics, Ann Arbor, USA, 1990, pp.273–282.
4. Landrini, M., and Campana, E., “Wave and Forces about a Turning Flat Plate”, Proceedings of the 10th International Workshop on Water Waves and Floating Bodies , Oxford, UK., 1995, pp.141–144.
5. Dawson, C.W., “A Practical Computer Method for Solving Ship-Wave Problems”, Proceedings of the 2nd International Conference on Numerical Ship Hydrodynamics , Berkeley, USA, 1977, pp.30–38.
6. Bollay, W., “A Non-linear Wing Theory and its Application to Rectangular Wings of Small Aspect Ratio”, Z. angew. Math. Mech., Bd. 19, No.1, 1939, pp.21–35.
7. Lan, C.E., “A Quasi-Vortex-Lattice Method in Thin Wing Theory”, Journal of Aircraft, Vol. 11, No.9, 1974, pp.518–527.
8. Jensen, G., Soeding, H., and Mi, Z.-X., “Rankine Source Methods for Numerical Solutions of the Steady Wave Resistance Problem”, Proceedings of the 16th Symposium on Naval Hydrodynamics, Berkeley, USA, 1986, pp.575–581.
9. Thieme, H., “Ueber Stroemungstechnische Grundlagen zur Bestimmung von Steuereigen-schaften ”, Schiff und Hafen, H.9, 1954, pp.510– 518
10. Van den Brug, J.B., Beukelman, W., and Prins, G.J., “Hydrodynamic Forces on a Surface Piercing Flat Plate”, Report Nr.325, 1971, Shipbuilding Laboratory, Delft University of Technology.
11. Yamasaki, K., Fujino, M., and Kawamura, T., “Hydrodynamic Forces Acting on the Three Dimensional Body Advancing on the Free Surface” , Journal of the Society of Naval Architects of Japan, Vol. 154, 1983, pp.305–313.
DISCUSSION
E.F.Campana
INSEAN, Italy
As a general comment, the present results by Dr. Zou seem to confirm the main conclusions of the paper by Dr. Landrini and myself which was presented at the Workshop on Water Waves and Floating Bodies (10th WWWFB) held in Oxford last year. There and in a subsequent paper [1] we showed some results concerning the steady drift and turning motion of a surface-piercing flat plate described by a linearized free-surface problem according to the Dawson procedure. In particular, by adopting a simplified but still nonlinear wake model, the relevant role of the keel vortex in determining the force coefficients was there emphasized.
I have a few specific comments on the paper included in the proceedings:
-
Concerning both trailing edge and tip vortices, we had used an iterative solution to adjust the direction of the trailing vortices with the “local” velocity. Have you already tried to follow that procedure? If not, in what sense is the model you considered nonlinear?
-
Dealing with the double body linearization, we experienced very sharp gradients of the second derivatives of the double body solution near the intersection between the leading edge of the plate and the undisturbed water plane. Although not adopting a low-pass filter, as suggested by Nakos and Sclavounos [2], we obtain satisfactory values for the convergence. What is your experience on that problem?
-
In the computation, we have found it useful to neglect the influence of the (perturbation) trailing vortex nearest to the free surface. This is because that vortex may generate a jerky behavior of the solution, being too close to the free surface collocation points. How do you handle this problem?
-
In our computations, increasing discrepancies between experiments and numerics were observed in the higher Froude range (see, for example, figure 9 in [3]). Could you please comment on this?
REFERENCES
[1] M.Landrini, E.F.Campana, “Steady Waves and Forces About a Yawing Flat Plate,” Journal of Ship Research, 1996. In press.
[2] D.E.Nakos, P.D.Sclavounos, “Kelvin Wakes and Wave Resistance of Cruiser and Transom-Ships, Journal of Ship Research, Vol. 38 , No. 1, pp. 9–29, 1994.
[3] A.DiMascio, M.Landrini, E.F.Campana, “On the Modeling of the Flow past a Free-Surface Piercing Flat Plate, ” 21st Symposium on Naval Hydrodynamics, Trondheim, Norway, this volume.
AUTHOR'S REPLY
-
The vortex model used in the present work is an extension of Bolley 's model which is nonlinear in the sense that the trailing vortices leave the plate at some angle to the plane of the plate and thus form a vortex sheet which does not lie in that plane. As the numerical results indicated, this vortex model is efficient to predict the nonlinear dependance of the hydrodynamic forces on drift angle and yaw rate.
-
For the linearized boundary condition on the free surface, derivatives of the double-body velocity potential up to the second order need to be calculated. In my calculation, for each drift angle or yaw rate only one free-surface grid is used. The inmost collocation points on the free surface lie at a small distance away from the intersection of the plate and the undisturbed free surface. I did not investigate the details of the flow near the leading edge.
-
The vortex distribution on the plate is discretized by a quasi-continuous method, resulting in a system of horseshoe vortices. The uppermost horseshoe vortices are between the inmost collocation points on both sides of the free surface and are included in the calculation.
-
In a potential-flow method for lifting problem, a Kutta condition is imposed at the trailing edge to fix the value of lift force which is ultimately due to viscosity. For a surface-piercing plate, the experimentally observed jump in the free-surface elevation across the wake just behind the trailing edge above some critical Froude number is contrary to the Kutta condition of pressure continuity. There, it cannot be expected that the potential-flow method would predict correctly the lift force at range of higher Froude number.











