The Influence of a Bottom Mud Layer on the Steady-State Hydrodynamics of Marine Vehicles
L.Doctors (Australian Maritime Engineering Cooperative Research Center, Australia), G.Zilman, T.Miloh (Tel-Aviv University, Israel)
Abstract
The work to be presented here is an extension of previous research into the influence of a uniform layer of silt or mud with a specified density and viscoelastic properties on the resistance of a marine vehicle undergoing rectilinear motion at a constant speed in water of finite and constant depth. The theory is therefore applicable to the wave-resistance and other hydrodynamic aspects of monohull and catamaran ferries in use on rivers as well as to landing craft in coastal regions. In these calculations, it is necessary to take into account both the finite width and the finite depth of the waterway.
In such physical situations, there are additional questions about the influence of a soft underlying layer of mud on the river bed, apart from the usual concerns regarding errors resulting from the use of a linearized inviscid theory. This theory had previously been applied to the following three cases: (a) an air-cushion vehicle (ACV) traveling over water with a muddy bed, (b) an ACV traveling over a muddy layer alone, and (c) a displacement vessel traveling over water with a muddy bed.
A principal feature of the analytic solution is that the wave resistance can be presented as the double integral over the longitudinal- and transverse-wavenumber domain. This result contrasts with the classic case of a purely inviscid flow in which the wave resistance can be expressed as a single integral over the wavenumber space, because there is a unique relationship between the two abovementioned wavenumbers. In physical terms, this corresponds to the fact that the wave resistance can be connected by means of an energy argument to the downstream wave system, since no energy is dissipated by viscous means. One can no longer utilize this discussion when there is an underlying mud layer, because of the resulting viscous dissipation.
Although the integrand is rather poorly behaved, exhibiting the expected wave-like oscillations with respect to the two wavenumbers, one can perform the numerical integrations and predict some very interesting results, particularly when the water is relatively shallow. For example, the peak resistance, which traditionally occurs when the depth Froude number is unity, now occurs at some speed which is intermediate between the speeds corresponding to unit values of the depth Froude number based on the upper water layer alone and based on the total combined depth of mud and water. Indeed, the whole curve of wave resistance as a function of the speed is, in some general sense, an average between those two limiting extreme cases; however, one can only properly determine the precise influence of the mud layer by means of the detailed calculations required by the new theory, as described here.
In the current work, the theory has been extended to permit the computation of the hydro-
dynamic sinkage force and trimming moment on the vessel. Calculations have been completed for a standard Wigley hull. Once again, it is observed from the numerical results that the influence of the mud layer on these force components is such as to suggest that the equivalent overall water depth lies somewhere between that of the water layer alone and that of the total mud-water domain, depending on the physical properties of the mud.
1
Introduction
1.1
Previous Work
During the last few years, there has been a renewed effort to develop a better hydrodynamic understanding of marine vehicles in water of finite depth. Such cases of interest include coastal regions, harbors, rivers, lakes, and ocean inlets. A particular case of concern is the effect of the overlaying mud layer in rivers on the hydrodynamics of fast moving craft (that is, at a depth Froude number greater than unity). Such an example is that of Australian river catamarans with a low keel clearance traveling in rivers and narrow channels with a movable muddy bed, with an average (length) Froude number of 0.65, and reported by Doctors, Renilson, Parker, and Hornsby [1].
The new physical feature of this problem, the subject of this paper, is the important effect of the underlying movable muddy sea bottom on the ship hydrodynamics. An example of recent work is that of Zilman and Miloh [2], which is applicable to slow ships (that is, moving in restricted water with a relatively low Froude number). They found that the compliance of the sea bottom has a profound effect on the hydrodynamic performance of such vessels when navigating in shallow water. In that work, the zero-Froude-number approximation was made; this resulted in the sea-surface being simplified and replaced by a rigid surface. Of course, the waves generated on the mud-water interface were modeled appropriately.
In the approximation used in that research, the mud was treated as a Newtonian viscous fluid. This approach had also been applied by Zilman, Miloh, and Kagan [3] to calculate the effect of mud viscosity on the added-mass and damping coefficients of two-dimensional ship cross sections undergoing periodic oscillations in the upper fluid layer.
This theoretical work on ship hydrodynamics in a two-layer environment was an outgrowth of earlier research in which the viscosity was ignored in both layers, but the effects of different densities were included. The results of such calculations were reported by Miloh, Tulin, and Zilman [4], where wave-drag calculations in a laterally unbounded domain were done.
More recently, the theory has been developed to the stage, where it is now analogous to the classical work of Michell [5] for a thin ship traveling in deep and inviscid water and that of Sretensky [6] for steady motion in a channel. That is to say, the traditional linearized free-surface conditions were used on both the sea surface and the mud-water interface by Zilman, Doctors, and Miloh [7]. The mud was modeled as a linear viscoelastic substance. The numerical test cases presented in that publication were applicable to an air-cushion vehicle (ACV) traveling over the sea with a muddy bottom, an ACV traveling over mud alone, and a ship traveling in a sea with a muddy bottom. The computations demonstrated interesting effects of the compliance of the mud with anticipated results in limiting cases, such as when the mud had either extremely low or high viscosity or stiffness.
One of the outcomes of the current research, naturally, is an ability to predict the sinkage and trim of a vessel. In reference, firstly, to purely inviscid hydrodynamics, we should acknowledge the pioneering theoretical work of Tuck [8], in which the shallow-water approximation was employed, and Tuck [9], where the influence of the finite-width of the channel was included in the analysis. Other work, of an experimental or empirical nature, was reported by Tuck [10], Dand and Ferguson [11], Barrass [12 and 13], Ferguson, Seren, and McGregor [14], and Ferguson [15].
Returning more to the subject of the current investigation, the significance of a silt-covered sea bed on the maneuvering characteristics of large vessels has been demonstrated by Sellmeijer and Oortmerssen [16] in a towing tank. Further work on this subject was reported by Vantorre [17], while a survey paper by d'Angremond, Deelen, and Vantorre [18] also described a number of experiments in which the mud properties, such as density, viscosity, and its rheology in general, were shown to be important.
1.2
Present Work
In the current work, we take the developmental work of Zilman, Doctors, and Miloh [7] one stage further, by computing all three of the components of generalized force on the vessel—that is, the wave resistance, sinkage force, and the bow-up moment.
In order to have an amenable model of these phenomena, we consider an upper layer of inviscid water on top of a second, and lower, layer of viscoelastic mud lying on a rigid horizontal bottom as shown in Figure 1(a). The fluid domain is also bounded by two vertical straight walls on each side, representing the walls of a channel or a towing tank. The two fluids are assumed to be immiscible and to be separated by the distinct mud-water interface. The vessel is immersed only in the upper layer and does not plough the interface.
As in the previous work discussed above, it is assumed that the sea-water mud behaves like a viscoelastic substance. To keep the analysis tractable, we will use here only a linear viscoelastic model, in which the shear stress is related to the rate of strain by a convolution-type integral, with the relaxation function serving as a kernel. The strong similarity between the gravitational waves generated by a moving ship and progressive surface sea waves allows us to use such a linear viscoelastic rheological model, previously suggested, for example, by Gade [19], Dalrymple and Liu [20], MacPherson [21], Hsiao and Shemdin [22], and Maa and Mehta [23].
Although, not used in the current work, the interested reader is referred to the studies of Foda, Hunt, and Chou [24], where nonlinear rheological aspects of the mud were considered.
2
Development of the Theory
2.1
Basic Hydrodynamic Equations
The coordinate system is shown in Figure 1(a). Here, an inertial reference frame is oriented so that the x axis is directed forward, the y axis is to port, and the z axis is measured vertically upward from the mud-water interface. The water has a density ρ and a depth d. As usual, the water is assumed to be both inviscid and incompressible.
Hence, the flow in the water layer is irrotational, which implies that there exists a velocity potential ![]() which satisfies the Laplace equation:
which satisfies the Laplace equation:
![]() xx+
xx+![]() yy+
yy+![]() zz=0 for 0<z<d. (1)
zz=0 for 0<z<d. (1)
The mud has a thickness d′ and is considered to be an incompressible viscoelastic medium. The general linearized equations of fluid motion in the mud layer for –d′<z<0 are:
(2)
![]() ·U=0, (3)
·U=0, (3)
where U denotes the three-component velocity vector, ρ′ is the density of the mud, t is the time, p′ is the total pressure and τ is the stress tensor.
For a Newtonian fluid, the shear stress depends linearly on the rate-of-strain tensor:
(4)
with the proportionality parameter being simply the dynamic viscosity.
2.2
Boundary Conditions
The usual linearized combined free-surface condition on the sea surface pertains to the problem under study here. It is
![]() tt+g
tt+g![]() z=0 for z=d, (5)
z=0 for z=d, (5)
in which g is the acceleration due to gravity.
The linearized kinematic boundary condition on the mud-water interface requires only that there is continuity of the vertical component of velocity w, because the water is considered to be a perfect fluid. That is:
(6)
The introduction of the unknown interface elevation ζ′ requires an additional relationship in the form of a dynamic free-surface condition, the Bernoulli equation, whose linearized form is
ρ![]() t+ρgζ′+pI=0 for z=0, (7)
t+ρgζ′+pI=0 for z=0, (7)
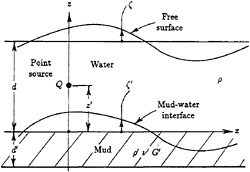
Figure 1: Problem Definition (a) Coordinate System
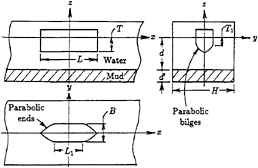
Figure 1: Problem Definition (b) Modified Wigley Hull
where pI(x,y) is the pressure acting at the interface. Zero shear stress in the two horizontal directions on the interface between the mud and the water requires the pair of conditions:
τyz=τxz=0 for z=0. (8)
It may also be noted that the three velocity components must vanish on the bottom of the mud layer. That is:
U(u,v,w)=0 for z=–d′. (9)
The assumption that the mud depth d′ is small compared with a typical horizontal length scale (such as the interfacial wave length) suggests, in general, that both u and v and their derivatives with respect to x and y can be considered large with respect to w and its corresponding derivatives. It also follows that the pressure variation within the mud layer is essentially hydrostatic. That is, the shallow-water approximation can be used:
p′(x,y,z)=ρ′g(ζ′–z)+pI(x,y). (10)
2.3
Solution for the Potential
The problem is now solved for the velocity potential ![]() for a point source of strength Q, located at the point (x′,y′,z′) in the water above the mud-water interface, as shown in Figure 1(a), in a frame of reference moving steadily in the positive x direction, with a constant velocity U. Due to the linearity of the problem, it is convenient to utilize a double Fourier transform, as explained by Zilman, Doctors, and Miloh [7]. The result of this analysis is:
for a point source of strength Q, located at the point (x′,y′,z′) in the water above the mud-water interface, as shown in Figure 1(a), in a frame of reference moving steadily in the positive x direction, with a constant velocity U. Due to the linearity of the problem, it is convenient to utilize a double Fourier transform, as explained by Zilman, Doctors, and Miloh [7]. The result of this analysis is:
(11)
where we have defined
(12)
(13)
and φ is regular and harmonic in the domain of interest (the upper inviscid fluid layer) and is given by the following set of formulas:
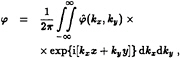
(14)
(15)
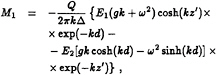
(16)
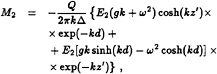
(17)
(18)
E1=1–![]() gd′k2δ/ω2, (19)
gd′k2δ/ω2, (19)
E2=(1–![]() )kd′δ, (20)
)kd′δ, (20)
and
δ≡1–tanh(γd′)/(γd′), (21)
(22)
![]() =1–ρ/ρ′, (23)
=1–ρ/ρ′, (23)
ω=Ukx, (24)
(25)
The “effective” or complex kinematic viscosity ![]() used in this analysis accounts for the viscoelastic nature of the mud; for the Kelvin-Voigt model employed in this work, we have
used in this analysis accounts for the viscoelastic nature of the mud; for the Kelvin-Voigt model employed in this work, we have
and this is equivalent to evaluating the shear stress according to the formula:
where e is the shear strain, the mud viscosity is µ′=ρ′v′, J=G′/ρ′, and G′ is the mud shear modulus.
2.4
Hydrodynamic Forces
The forces generated by the disturbance are defined as the relevant integrals of the normal stress over the surface area that characterizes the vehicle. For a displacement ship (that is, a body which is either partly or fully submerged), the required area is the area of the wetted surface.
The effect of the action of the vessel on the water can be reduced to the action of a source distribution with a density depending on the form of the vessel and the geometry of the channel. In the case of the classic thin ship, the source density has the interpretation of strength per unit area on the centerplane y=0 of the vessel. If the local beam of the vessel is b(x,z), the source density is given by Michell's form as
(26)
The wave resistance RW, the sinkage force SW, and the bow-up moment MW (the three components of the generalized force) will be denoted symbolically by the notation ![]() and are defined in the usual way:
and are defined in the usual way:
(27)
where S0 is the centerplane area and p is the pressure on the surface of the hull, given by the linearized Bernoulli equation:
p=ρU![]() x, (28)
x, (28)
in which the hydrostatic-pressure component is ignored. Finally, the generalized hull slope in Equation (27) is just
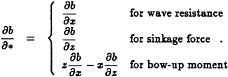
(29)
We are now in a position to collect the above formulas in the traditional manner needed for a wave-resistance calculation. The generalized force is given by Equation (27), into which the pressure from Equation (28) and the gradients from Equation (29) are substituted. It is also necessary to utilize the potential for a point source in Equation (11) and its associated equations, together with the source strength in Equation (26). For this purpose, it is necessary to keep in mind that Equation (11) applies to a point source located directly above the origin, so that a simple translation of the frame of reference for the source is also required.
After the usual manipulations, one can obtain the following formula for the induced generalized forces on the vessel:
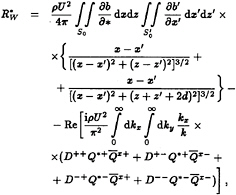
(30)
where the four coefficients are
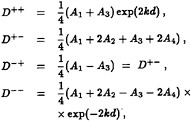
which are, in turn, given by the four formulas:
A1=E1(gk+ω2) exp(–kd)/Δ,
A2=–E2[gk cosh(kd)–ω2 sinh(kd)]/Δ,
A3=E2(gk+ω2)exp(–kd)/Δ,
A4=E2[gk sinh(kd)–ω2 cosh(kd)]/Δ.
The wave functions in Equation (30) are given by
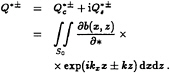
(31)
The prime ′ in Equation (30) is used to denote variables in the source domain, while unprimed variables refer to those in the field domain.
The three major terms in this equation correspond to the three terms in Equation (11). The first two (source) terms do not contribute to the first component of the generalized force (the wave resistance) following d'Alembert's paradox. Additionally, the first two terms do not contribute to the third component (the bow-up moment) for a ship with fore-aft symmetry, such as the Wigley hull, to be considered later in the current work.
The fact that Equation (30) gives the forces in terms of a double integration over the wavenumber domain (kx,ky) is an indication that, in the physical problem, all such wave components contribute to these forces. This is in contrast to the classic inviscid case where one can use a far-field argument to demonstrate that only a one-dimensional spectrum of waves exists downstream.
In the limiting case of an infinitely deep upper layer (that is, d → ∞), Equations (30) and (31) simplify to the classic result for a thin ship moving in deep water.
2.5
Influence of the Tank Walls
The influences of the tank walls can be incorporated by introducing “image” source distributions with a lateral spacing of the tank width H, which satisfy the tank-boundary condition, namely
v=0 for y=±H/2. (32)
Thus, one must consider the infinite sum of functions of the type used in Equation (11). Regarding the third, or wave, term in Equation (30), the result can be simplified using the Poisson summation formula and this procedure has been followed by a number of researchers in similar circumstances.
The final result for the formula for the induced generalized forces on a vessel moving in a channel is
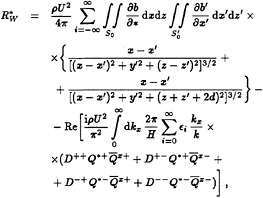
(33)
in which
y′=iH, (34)
(35)
ky=2πi/H. (36)
The wavenumber index i has been omitted from all the variables in Equation (33), for the sake of brevity. It is observed that one can simply replace the integration with respect to the transverse wavenumber ky in the third term by a summation, in which one effectively evaluates the integral by the trapezoidal formula with the abscissas provided by Equation (36).
2.6
Classic Case of a Rigid Bed
An important question is that relating to the behavior of Equations (11) to (25) in certain limiting cases. Thus, a careful examination of these formulas does indeed reveal that in the case of vanishing mud complex kinematic viscoelasticity ![]() (together with the assumption of ρ′/ρ=1), the classic case of inviscid wave resistance in water of depth d+d′ is recovered; the standard formula for the potential was published by Sretensky [6] and Lunde [25]. In a similar vein, if either the mud complex kinematic viscoelasticity
(together with the assumption of ρ′/ρ=1), the classic case of inviscid wave resistance in water of depth d+d′ is recovered; the standard formula for the potential was published by Sretensky [6] and Lunde [25]. In a similar vein, if either the mud complex kinematic viscoelasticity ![]() or the mud density ρ′ approaches infinity, then the classic inviscid case corresponding to a water depth d is obtained, as expected. This behavior will also be demonstrated here by the computed results.
or the mud density ρ′ approaches infinity, then the classic inviscid case corresponding to a water depth d is obtained, as expected. This behavior will also be demonstrated here by the computed results.
3
Results
3.1
Wave Functions
A hull, patterned after that proposed by Wigley [26], was used in the current work. The vessel is depicted in Figure 1(b) and its local beam b(x,z) is defined in the following manner, for positive x:
b(x,z)=BF(x)(x)F(z)(z), (37)
(38)
(39)
in which H(x) is the Heaviside step function and
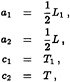
and L is the length, B is the beam, and T is the draft. Finally, L1 is the length of parallel middle body and T1 is the depth of the wall-sides.
The wave functions for this vessel, defined by Equation (31), can be determined analytically, as follows:
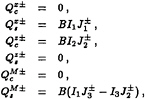
in which the new integrals are
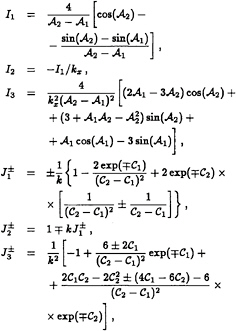
where
A1=kxa1,
A2=kxa2,
C1=kc1,
C2=kc2.
3.2
Numerical Details
The first term in Equation (33) was evaluated numerically in a straightforward manner. That is to say, the centerplane areas S0 and ![]() were divided into rectangular patches and the integrations computed using the midpoint rule. A typical choice of integration parameters was 204 patches in the
were divided into rectangular patches and the integrations computed using the midpoint rule. A typical choice of integration parameters was 204 patches in the
x and x′ directions and 18 patches in the z and z′ directions. Longitudinal symmetry was used to halve the actual computation. A conservative measure of the error in this calculation was obtained by comparing the result with that obtained using one-third the number of patches in the two centerplane directions, for which the midpoint rule could also be used without any further computation of the integrand. The abovementioned choice of parameters led to an integration error of less than one percent. It is also important to note that the numerical integration only has to be done once for any particular geometric configuration, since the numerical value of this term varies simply with the square of the speed of the ship U.
With regard to the image source distributions needed to model the influence of the tank walls, a typical selection was 65 images (that is, the original, central, vessel plus 32 on each side), for the case H/L=1, which also led to an error of around one percent.
The second term in Equation (33) was calculated in conjunction with the first term, as implied by the algebraic grouping used there.
There is no doubt that these first two terms can be computed analytically for a Wigley-style hull, as an exploratory investigation confirmed. However, the resulting algebra would clearly be very error prone and the required effort quite excessive.
The double integral for the third term in Equation (33) was evaluated by means of the trapezoidal rule applied in the two directions of the (kx,ky) wavenumber domain. This approach had the advantage that it was both easy to program and that one could also obtain the result for laterally restricted water using the same method (just by selecting the appropriate spacing in the transverse-wavenumber direction ky, given by Equation (36)).
One should be interested in four estimates of the errors in this numerical procedure. These are the two truncations errors, resulting from not carrying out the summations to infinity in Equation (33), and the two errors associated with using a finite step size.
The computer program was written to evaluate these four errors in a straightforward manner. Firstly, the generalized forces were computed from user-supplied values of the two truncation points and the two step sizes. In addition, the program computed the forces four additional times, using (in turn) half the values of the truncation points or twice the step size, as the case may be. These additional calculations require negligible additional effort, since the integrands have already been determined.
The estimate of the error was then given by the relevant differences in these calculations. These estimates are, of course, quite conservative and a number of experiments was conducted to show that it is indeed safe to use them. It should be added that the “error” related to using different step sizes in the transverse wave number corresponds to the difference in generalized forces when running in channels of the relevant different widths; it can be used to estimate the restrictive influence of finite channel width.
Previous experience with oscillatory integrals with an infinite range of this nature has shown that it is difficult to improve on the procedure outlined here. Generally speaking, there was no difficulty in obtaining well converged results, except that the computer time became rather excessive and the specified errors in the generalized forces had to be relaxed to around one percent. Even so, very large numbers of points were often required. That is, truncation values of kxL=20 and kyL=80 were needed. These led to a requirement of up to 16×106 points in the kx direction and 50 points in the ky direction, for a tank-width-to-ship-length ratio H/L of 4.
3.3
Forces on a Vessel
The set of computed results to be presented here pertains to the Wigley hull form defined by Equations (37) to (39). The vessel has a beam-to-length ratio B/L of 0.1 and a draft-to-length ratio T/L of 0.0625. The water-depth-to-length ratio d/L was chosen to be 0.2 and the dimensionless mud-thickness d′/L was taken to be 0.1. A set of dimensionless tank widths H/L of 0.25, 0.5, 1, and 2 was considered in the calculations.
The usual three coefficients of the generalized force for a ship have been used in the plots.
That is:
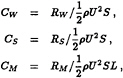
where S is the wetted-surface area. For our selected vessel, the computed dimensionless wetted-surface area S/L2 is 0.14879. For the abscissa, the inverse-square-Froude-number parameter:
A=1/2F2=gL/2U2,
was chosen. This has the advantage (over using the Froude number ![]() as the standard abscissa) of conveniently stretching the horizontal scale at low speeds, allowing one to study the oscillations in the wave-resistance curve more easily.
as the standard abscissa) of conveniently stretching the horizontal scale at low speeds, allowing one to study the oscillations in the wave-resistance curve more easily.
Computed data for five different types of mud were produced and the results for these cases appear in all of the figures. The properties for each of these muds appear in Table 1. In a qualitative sense, the muds range, in progression, from “loose” to “solid”. Thus, Mud 1* has no viscosity at all. This case represents the classic inviscid situation. Results for this case were obtained from that theory with a dimensionless depth of 0.3. Mud 1 has a very low viscosity, causing it to behave almost like water; it was used to test the operation of the current computer program, by comparing the results with those from Mud 1*. Mud 2 possesses an intermediate viscosity. Mud 3 possesses both an intermediate viscosity and elasticity. Mud 4 is similar to Mud 3, but has twice the density. Next, Mud 5 has a very high viscosity, resulting in it behaving essentially like a solid. Finally, Mud 5* is the second limiting case. Solutions were obtained by using the classic theory with a dimensionless depth of 0.2.
The four parts of Figure 2 show the wave resistance in a channel whose dimensionless widths are 0.25, 0.5, 1, and 2, respectively. We first examine Figure 2 (a) for the case of a dimensionless channel width of 0.25. The most striking feature of these results is the well-known jump in the resistance at the critical value of unity of the depth Froude number ![]() which is seen for the two limiting cases, namely Mud 1 and Mud 5. The first limiting case is that of a very low value of the dimensionless mud viscosity
which is seen for the two limiting cases, namely Mud 1 and Mud 5. The first limiting case is that of a very low value of the dimensionless mud viscosity ![]() of 10–5. In this case, the mud behaves like (inviscid) water and
of 10–5. In this case, the mud behaves like (inviscid) water and
Table 1: The Five Types of Mud
|
Mud |
Density ρ′/ρ |
Viscosity
|
Elasticity G′/ρgL |
|
1* |
1 |
0 |
0 |
|
1 |
1 |
10–5 |
0 |
|
2 |
1 |
10–2 |
0 |
|
3 |
1 |
10–2 |
10–2 |
|
4 |
2 |
10–2 |
10–2 |
|
5 |
1 |
100 |
0 |
|
5* |
1 |
∞ |
0 |
the effective depth is d+d′, causing the discontinuity to occur at a speed parameter of 5/3.
The matter of this discontinuity has been discussed many times in the literature, in particular, by Lunde [25]. The sudden loss of the transverse component of the wave system leads to a drop in the resistance, whose magnitude is given by
ΔRW=3W2/2ρgHd2, (40)
in which W is the weight of the vessel.
The phenomenon of the drop in resistance is related to the energy carried by the transverse wave, which no longer exists as part of the spectrum of waves generated by the moving disturbance. This wave cannot, of course, travel faster than the critical speed. Experimental work confirms both the location (that is, the Froude number) and the magnitude (the value of the discontinuity in the resistance), provided the water is not too shallow and the ship is reasonably thin. Otherwise, the assumptions in the theory are violated and both viscous and nonlinear effects tend to limit the magnitude of the jump, as well as rounding its sharp (or sudden) characteristic.
Returning, now, to Figure 2(a), the results from a traditional wave-resistance program for Mud 1* (zero mud viscosity) are also provided and these appear as a dotted curve. Almost perfect agreement can be seen. One should not expect precise concurrence here for three reasons; firstly (as noted already) the current program cannot be run for the purely inviscid case; secondly, the current program requires an integration with respect to the longitudinal wavenumber (as noted in Equation (33)), which is not required in classic wave-resistance calculations; and thirdly, the fluid dynamics of the mud are modeled in the present research using the so-called “shallow-water” approx-
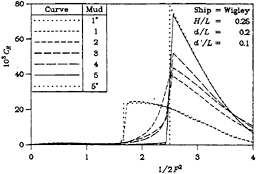
Figure 2: Wave Resistance
(a) H/L=0.25
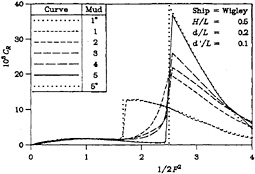
Figure 2: Wave Resistance
(b) H/L=0.5
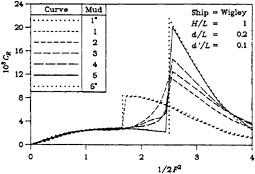
Figure 2: Wave Resistance
(c) H/L=1
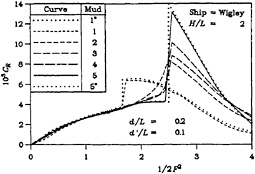
Figure 2: Wave Resistance
(d) H/L=2
imation, which is evidently quite accurate relative to the finite-depth theory, in this example.
Similarly, for a very high dimensionless viscosity of 100, the case of Mud 5, one would expect the mud to behave as an immovable solid, thus providing us with the other limit of the classic inviscid case, namely Mud 5*, with a dimensionless depth of 0.2, whose critical speed occurs when the speed parameter equals 5/2. The numerical results correctly confirm this behavior.
Figure 2(a) shows other, intermediate, cases, as well. Thus, for Mud 2 with a dimensionless mud viscosity of 10–2, a result somewhat midway between the abovementioned two extremes is observed. Furthermore, by also including mud elasticity, as for Mud 3, with a dimensionless value G′/ρgL of 10–2, the mud is seen to exhibit an even more solid behavior than when the viscosity alone is modeled. The next intermediate case, that of Mud 4, utilizes the same values of mud viscosity and shear modulus, but also includes now a higher dimensionless density ρ′/ρ, with a value of 2. This fourth case produces results approaching those of the previously noted instance of an almost solid mud layer, that of Mud 5.
Next, we discuss here the results for the wave resistance displayed in Figures 2(b), (c), and (d), corresponding respectively to dimensionless tank widths of 0.5, 1, and 2. The comments made regarding Figure 2(a) apply in these cases, too. The essential difference is that the behav
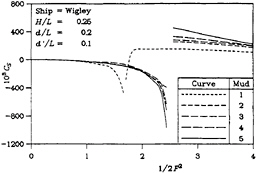
Figure 3: Sinkage Force
(a) H/L=0.25
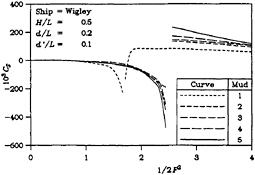
Figure 3: Sinkage Force
(b) H/L=0.5
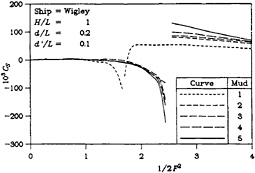
Figure 3: Sinkage Force
(c) H/L=1
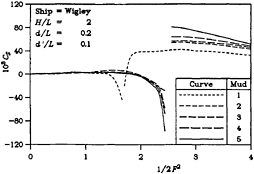
Figure 3: Sinkage Force
(d) H/L=2
ior of the curves is much more moderate, due to the greater tank widths under consideration. This point is epitomized by Equation (40), which states that the jump is inversely proportional to the channel width.
The four parts of Figure 3 show the sinkage force for the same four dimensionless tank widths. The general behavior is one in which the more solid mud yields results with more extreme behavior, particularly near the critical depth Froude number, as already discussed in the case of wave resistance.
Again, somewhat similar behavior can be seen in the four parts of Figure 4 for the bow-up moment, in the sense that the cases of a more solid mud generate curves with a stronger behavior.
3.4
Sinkage and Trim
It is straightforward to estimate the dependence of the sinkage s and bow-up trim t on the speed U of the vessel. Within the framework of linearized hydrostatics, which is consistent with the hydrodynamics employed here, the dimensionless sinkage and trim are given by the two formulas:
(41)
(42)
in which IW is the longitudinal second moment of the waterplane area AW. For this purpose, we have assumed that the longitudinal metacentric height ![]() can be approximated by the longitudinal
can be approximated by the longitudinal
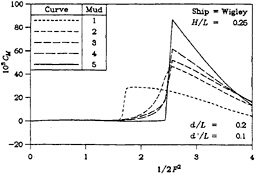
Figure 4: Bow-Up Moment
(a) H/L=0.25
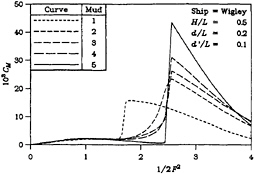
Figure 4: Bow-Up Moment
(b) H/L=0.5
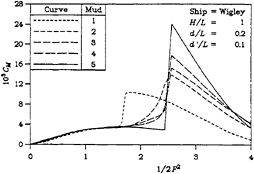
Figure 4: Bow-Up Moment
(c) H/L=1
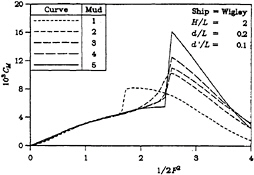
Figure 4: Bow-Up Moment
(d) H/L=2
metacentric radius ![]() For a standard Wigley hull, these two formulas become:
For a standard Wigley hull, these two formulas become:
s/L=1.116CSF2,
t/L=22.32CMF2.
Figure 5 show the sinkage of the vessel in question for the four dimensionless tank widths under consideration. The curves for sinkage strongly resemblance the previously discussed curves of sinkage force.
Finally, the bow-up trim is plotted in Figure 6. In the same way, the curves of bow-up trim are closely related to the curves of bow-up moment. So, one can see the discontinuities at the critical depth Froude number and also observe the fact that the magnitudes of the discontinuities are greater when the mud is more solid and/or when the channel is narrower.
By way of comparison, it is instructive to consult the work of Tuck [8]. The current results for sinkage and bow-up trim bear a strong relationship to those of his calculations, particularly in regard to the singular behavior. However, exact conclusions cannot be drawn, because of the various additional simplifying assumptions made in his work—particularly that of infinite tank width. Furthermore, it is encouraging to note that the experimental data that he presented is even more in accordance with the results shown here. In his later paper, Tuck [9] did investigate the very strong effect of finite channel width, which is always to in-
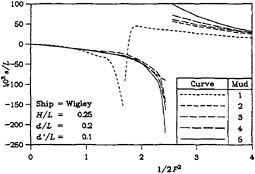
Figure 5: Sinkage
(a) H/L=0.25
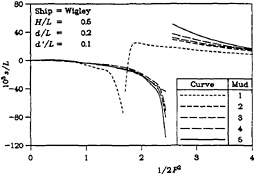
Figure 5: Sinkage
(b) H/L=0.5
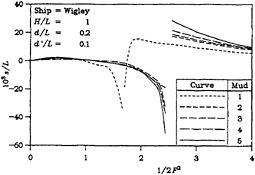
Figure 5: Sinkage
(c) H/L=1
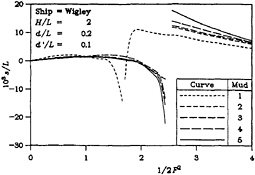
Figure 5: Sinkage
(d) H/L=2
crease the magnitude of the results, as confirmed by the present work.
4
Concluding Remarks
The analysis using the Kelvin-Voigt model implemented in this paper shows that the generalized forces due to a disturbance moving in the water layer above a dense mud layer depend strongly on the parameters of such a two-layer system. The most important feature of the curves for the forces is that the maximal values are not always a monotonic function of the mud density, mud viscosity, or elasticity.
The role of the mud viscosity is not obvious. On the one hand, the dissipation of the fluid energy in the lower viscous layer results in a decrease of the wave resistance. On the other hand, for a relatively large mud viscosity, such a dissipation can be negligibly small (the limiting case of infinitely large viscosity is a good illustration of this statement). Thus, roughly speaking, the resulting effect of the mud viscosity, at least in the vicinity of the maximal value of the wave drag, can be interpreted as an effective reduction in the total depth of the water.
It is almost universally true that the mud properties have a profound influence on the three components of the generalized force for subcritical speeds (Fd<1). However, at least for the
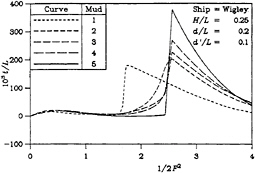
Figure 6: Bow-Up Trim
(a) H/L=0.25
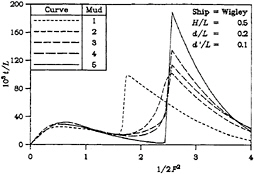
Figure 6: Bow-Up Trim
(b) H/L=0.5
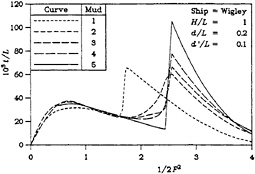
Figure 6: Bow-Up Trim
(c) H/L=1
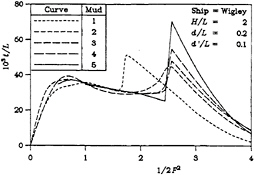
Figure 6: Bow-Up Trim
(d) H/L=2
range of mud properties used in the present calculations, there is much less effect at supercritical speeds (Fd>1), suggesting that the mud has less chance to respond to the hydrodynamic pressures at these higher speeds.
Certainly, for intermediate values of the mud properties, the general effects of the mud layer are to moderate any distinct features of the traditional linearized wave-resistance theory. One might therefore surmise that at least one explanation has been found for imperfect agreement between predictions and measurements of ship resistance in a river. Other reasons may, of course, include nonlinear effects and wave breaking.
Future work in this area of research will include the computation of the elevation of the interfacial wave so that the likelihood of grounding of the vessel can be estimated.
5
Acknowledgments
Prof. H.Söding of Hamburg University discussed many practical aspects of this problem with the authors. In addition, they would like to acknowledge the support of the Australian Maritime Engineering Cooperative Research Centre (AMECRC) (to which the first author is on partial secondment from The University of New South Wales) and Tel-Aviv University, as well as that of the Germany-Israel Foundation under Contract Number I-200–168.10.
6
References
[1] DOCTORS, L.J, RENILSON, M.R., PARKER, G., AND HORNSBY, N.: “Waves and Wave Resistance of a High-Speed River Catamaran”, Proc. First International Conference on Fast Sea Transportation (FAST '91), Norwegian Institute of Technology , Trondheim, Norway, Vol. 1, pp 35–52 ( June 1991)
[2] ZILMAN, G. AND MILOH, T.: “Hydrodynamics of a Body Moving over a Mud Layer—Part 1: Wave Resistance”, J. Ship Research, Vol. 39, No. 3, pp 194–201 ( September 1995)
[3] ZILMAN, G., MILOH, T., AND KAGAN, L.: “Hydrodynamics of a Body Moving over a Mud Layer”, Twentieth Symposium on Naval Hydrodynamics, University of California, Santa Barbara, California, 17 pp ( August 1994)
[4] MILOH, T., TULIN, M.P., AND ZILMAN, G.: “Dead-Water Effects of a Ship Moving in Stratified Seas”, J. Offshore Mechanics and Arctic Engineering, Trans. American Society of Mechanical Engineers, Vol. 115, No. 2, pp 105–110 ( May 1993)
[5] MICHELL, J.H.: “The Wave Resistance of a Ship”, Philosophical Magazine, London, Series 5, Vol. 45, pp 106–123 ( 1898)
[6] SRETENSKY, L.N.: “On the Wave-Making Resistance of a Ship Moving along in a Canal”, Philosophical Magazine, Series 7, Supplement , Vol. 22, No. 150, pp 1005–1013 ( November 1936)
[7] ZILMAN, G., DOCTORS, L.J., AND MILOH, T.: “The Influence of a Bottom Mud Layer on the Resistance of Marine Vehicles ”, Ship Technology Research: Schiffstechnik, Vol. 43, No. 2, pp 51–61 ( May 1996)
[8] TUCK, E.O.: “Shallow-Water Flows past Slender Bodies”, J. Fluid Mechanics, Vol. 26, Part 1, pp 81–95 ( September 1966)
[9] TUCK, E.O.: “Sinkage and Trim in Shallow Water of Finite Width”, Schiffstechnik, Vol. 14, No. 73, pp 92–94 ( 1967)
[10] TUCK, E.O.: “The Estimation of Squat”, Navigation, J. Australian Institute of Navigation, Vol. 3, No. 3, pp 321–324 ( December 1970)
[11] DAND, I.W. AND FERGUSON, A.M.: “The Squat of Full Ships in Shallow Water” , National Physical Laboratory, Ship Division, Report 175, 19 pp ( December 1973)
[12] BARRASS, C.B.: Ship Squat, Lorne & MacLean Marine Publishers, Luton, England, First Edition, 24+iv pp ( October 1978)
[13] BARRASS, C.B.: “The Phenomena of Ship Squat”, International Shipbuilding Progress, Vol. 26, No. 294, pp 44–47 ( February 1979)
[14] FERGUSON, A.M., SEREN, D.B., AND MCGREGOR, R.C.: “The Prediction and Practical Measurement of Ship Squat in Shallow Water”, Proc. Conference on Marine Safety, University of Glasgow, 19 pp ( September 1983)
[15] FERGUSON, A.M.: “An Extrapolation Method for Ship Resistance Based on the Variation of Sinkage and Trim with Froude Number”, Trans. Royal Institution of Naval Architects, Vol. 126, pp 17–30, Discussion: 30–32 ( December 1984)
[16] SELLMEIJER, R. AND VAN OORTMERSSEN, G.: “The Effect of Mud on Tanker Manoeuvres”, Trans. Royal Institution of Naval Architects, Vol. 126, pp 105–120, Discussion: 120–124 ( December 1984)
[17] VANTORRE, M.: “Ship Behaviour and Control in Muddy Areas: State of the Art”, Proc. Conference on Manoeuvring and Control of Marine Craft (MCMC '94), pp 59–74 ( September 1994)
[18] D'ANGREMOND, K., DEELEN, C., AND VANTORRE, M.: “Nautical Depth Approach”, Initial Report of the Joint Working Group 30, Permanent International Association of Navigation Congresses (PIANC), International Association of Ports and Harbours (IAPH), 17 pp ( February 1994)
[19] GADE, H.G.: “Effects of a Nonrigid, Impermeable Bottom on Plane Surface Waves in
Shallow Water” , J. Marine Research, Vol. 16, No. 2, pp 61–82 ( 1958)
[20] DALRYMPLE, R.A. AND LIU, P.L.-F.: “Waves over Soft Muds: A Two-Layer Fluid Model”, J. Physical Oceanography, Vol. 8, No. 6, pp 1121–1131 ( November 1978)
[21] MACPHERSON, H.: “The Attenuation of Water Waves over a Non-Rigid Bed” , J. Fluid Mechanics, Vol. 97, Part 4, pp 721–742 ( April 1980)
[22] HSIAO, S.V. AND SHEMDIN, O.H.: “Interaction of Ocean Waves with a Soft Bottom”, J. Physical Oceanography, Vol. 10, No. 4, pp 605–610 ( April 1980)
[23] MAA, J.P.-Y. AND MEHTA, A.J.: “Soft Mud Response to Water Waves”, J. Waterway, Port, Coastal, and Ocean Engineering, Vol. 116, No. 5, pp 634–650 ( September/October 1990)
[24] FODA, M.A., HUNT, J.R., AND CHOU, H.-T.: “A Nonlinear Model for the Fluidization of Marine Mud by Waves”, J. Geophysical Research, Vol. 98, No. C4, pp 7039–7047 ( April 1993)
[25] LUNDE, J.K.: “On the Linearized Theory of Wave Resistance for Displacement Ships in Steady and Accelerated Motion”, Trans. Society of Naval Architects and Marine Engineers, Vol. 59, pp 25–76, Discussion: 76–85 ( December 1951)
[26] WIGLEY, W.C.S.: “A Comparison of Experiment and Calculated Wave-Profiles and Wave-Resistances for a Form Having Parabolic Waterlines”, Proc. Royal Society of London, Series A, Vol. 144, No. 851, pp 144–159+4 plates ( March 1934)
DISCUSSION
W.W.Schultz
University of Michigan, USA
Your potential flow upper layer ensures zero shear stress on the mud interface. How would you expect your conclusion to change if you added a boundary-layer at the interface to get the more realistic condition of high stresses?
AUTHORS' REPLY
We are grateful for Professor Schultz's discussion of our paper, as well as the other verbal discussion that took place after the presentation.
In summarizing our work, the mud layer is modeled as a viscoelastic substance and the flow is considered to be laminar. The concept of linearization of the problem, on the assumption of a small input disturbance, is quite realistic since the particle motions in both the mud and the water are small.
This smallness of motion implies that the boundary-layer effects at the mud-water interface would be unimportant. We therefore believe that the boundary layer in the water on top of the interface would not greatly affect the forces on the vessel—in the same way that the boundary layer in the bottom of a towing tank or a river (even in the case of relatively shallow water) is unlikely to have a significant influence on the predictions for the forces.
An interesting extension of this work would be to analyze a multilayer problem, so that the case of an indistinct interface could be studied. The principles are identical to those expounded in the paper, but the algebra and the corresponding computer program would be far more complicated.
















