Effect of Ship Motion on DD-963 Ship Airwake Simulated by Multizone Navier-Stokes Solution
T.Tai (David Taylor Model Basin, USA)
Abstract
The airwake about a DD-963 ship configuration is simulated by using a multi-zone, thin-layer Navier-Stokes method. The ship's superstructure is modelled by two blocked structures, followed by a flight deck and a lower missile deck. The ship motion is represented by change of ship attitude in a steady state flow environment. Two ship attitudes are considered: (1) the ship at two-degree pitch, and (2) the ship at one-degree pitch and five-degree roll. The freestream has a wind speed of 15.44 m/s (30 knots) at a direction of 30 degrees. The flow is fully turbulent with a Reynolds number of 177 million based on ship length. In general, the flow is largely separated behind the superstructure. The ship pitched bow down yields an airwake thinner than that of a ship at even keel traveling at the same speed. The ship with pitch or roll has larger local reversed flow regions characterized by backward-facing-step type flow.
Introduction
It is well known that the interface of aircraft/helicopter and ship poses problems in operability and survivability for naval aviation. Current aircraft/helicopter operations aboard the ship are characterized by restrictions due to weather and the need to often alter the ship 's course into the wind to establish necessary wind-over-the-deck conditions for a successful landing. The interface environment becomes more complicated by the presence of massive, turbulent airwake from the ship's superstructure. The technical issues here involves aspects concerning both the air vehicle and the ship. For aircraft, the lift characteristics become very sensitive to the surrounding environment due to relatively low freestream velocity and use of high lift devices. In case of the rotorcraft, the controllability in the final approach and landing is greatly influenced by the ship airwake.
The ship airwake is defined as an arbitrary volume of air, namely an air burble, surrounding the ship. The effect of airwake on the aircraft/ship interface operation is determined by the airflow disturbances caused by the ship that are perceptible to the pilot, and the final approach and landing patterns required for shipboard operation. Alleviation of the airwake effect would improve operability of the aircraft in a seabase interface environment [1–7].
The complexity of the problem requires use of the Navier-Stokes type method to reveal correct flow features. Advances in numerical algorithm schemes along with increased computer speed and capacity have made the computational fluid dynamics (CFD) feasible to provide answers to complex aerodynamic problems. Although physical modeling of unsteady, vortex dominated flows over complex geometry remains prohibitive, reasonably accurate simulated results based on steady-state solutions have been obtained during the past decade. Tai and Carico [8] applied three-dimensional, implicit finite-volume type Reynolds-averaged Navier-Stokes (RANS) scheme to consider the airwake problem behind a simplified DD-963 ship configuration. Computed viscous flow results have demonstrated good correlation with measurements. Later, Tai [9] simulated the airwake flowfield about a LPD ship with rather complex surface geometry representation and obtained reasonably useful steady-state flow results.
The present effort is an extension of previous work on the DD-963 ship airwake [8] to include the effect of ship motion. The ship motion is represented by change of ship attitude in a steady-state flow solution. The same multi-zone, RANS scheme used in Ref. 8 is employed with enhanced grid in the simulation.
Simulation Method
The simulation method, or the computational method employed includes two main elements: 1) the grid generation and 2) the flow solving. The description of the method therefore will be centered around these two topics, which are of equal importance.
Grid Generation and Grid Topology
A structured, curvilinear, body-conforming grid is generated. First, a surface grid is constructed from the designer's blueprint. The forward and midship superstructures are represented by two numerical blocked structures, followed by a flight deck, and a lower missile deck. The numerical model for the surface grid is derived by using the Tai simplification scheme called the area-volume rule for representing the surface components of a ship [10], see Fig.1. Computationally, the model consists of a
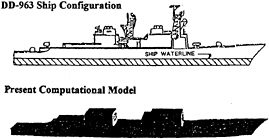
Fig. 1—DD-963 ship configuration.

Fig. 2—Ship model with 2-degree pitch (bow down)
serials of rectangular volume blocks in tandem. The ship model is then pitched and/or rolled with respect to the base plane that coincides with the water surface. Pitch was performed about the center of gravity and roll about the ship centerline through the center of gravity. Figure 2 shows the ship attitude (forward portion only) when it pitches two degrees into the water (bow down).
The NASA Ames 3DGRAPE code [11] is used for basic grid generations. A cylindrical grid topology is adopted for its capability to treat a body with a sharp nose. The topology is basically an H-O mixed type, with H-type in the longitudinal plane, and O-type in the crossflow plane. The outer cylindrical surface is set at 2.5 ship lengths from the ship centerline. The most forward plane is set at 1.0 ship length from the bow of the ship, and 3.0 ship lengths for the wake. Assuming symmetry about the centerplane, only half of the ship needs to be modeled in constructing the surface grid. The half model is then unfolded to whole ship in generating the volume grid. This size has been employed in other configurations and proved to be adequate.
An overall coarse grid is generated first by 3DGRAPE using a multi-block procedure. The radial distances are then clustered near the surface and stretched in the outer region for shear layer development. The complete grid has a total of 99×59×57 points with 57 points in the radial direction. This number is larger than those for aircraft because of very low speed freestream involved in the present work. Previous study [12] indicates that when using a compressible flow code at low Mach numbers, an increased mesh density is needed. The details of the grid generation and advantage of the grid topology adapted were discussed in Ref. 8. The grid resolution was enhanced by increasing the number of normal points from previous 51 points to 57 points in the present extension.
Flow Solver
The NASA Langley thin-layer Navier-Stokes code, namely the CFL3D code [13] with multi-zone capability, is used as the basic flow solver. Appropriate modifications to the code for applying specific boundary conditions are implemented. The code is based on a finite volume algorithm with a spatially factored diagonalized, implicit scheme for discretizing the three-dimensional, Reynolds
averaged Navier-Stokes equations. The upwind-biased differencing technique is used for the inviscid terms and central differencing for all viscous terms. The method is globally second-order accurate and well suited for patched grids in a multizone domain. Details are given by Thomas et al [13].
The code is upgraded with a variety of turbulence models, including the basic Baldwin and Lomax algebraic model [14], the one-equation models [15,16], along with the standard two-equation models, among others. These turbulence models have been carefully examined and evaluated by Rumsey and Vatsa [17]. In the present work, the Baldwin and Lomax model with a Degani-Schiff type modifications [18] is used. The modification determines proper length scales for separated flows.
Boundary Conditions
The boundary conditions for the Navier-Stokes flow solver are: 1) atmospheric boundary layer flow at upstream, 2) atmospheric pressure recovery at downstream, 3) characteristic form of inflow-outflow condition at the cylindrical outer boundary, and 4) viscous nonslip flow at the surface of the ship. The atmospheric boundary layer is approximated by a power-law profile:
V/V∞=(z/h)n (1)
where h is reference height and n varies from 0.10 to 0.14 [19]. The h is set to be the height of flight deck above the water surface, h=0.061 ship length, and n is set to its mean value of 0.12.
At downstream, instead of imposing the usual freestream recovery, the static atmospheric pressure condition is satisfied along with velocity components being extrapolated from the interior. The use of characteristic form of inflow-outflow boundary condition at the cylindrical outer boundary is known to improve convergence of solution at low speed.
The water surface is assumed to be flat and waveless at which the flow properties in the airwake remain unmixed with the water. The assumption makes the water surface neither viscous nor inviscid. Thus, a reflective boundary is applied. The application in fact is a post-priori after some other attempts of treating the water boundary failed. It turns out to be a good approximation after all except that the vertical velocity component must vanish at the water surface.
Wind Direction Coordinates
It is useful to define the wind direction coordinate system used in the present work. The wind direction is measured with respect to the ship's centerline. With reference to the sketch shown in Fig.3, the 0-degree indicates a head wind coming over the bow, 90-degree coming over the starboard beam, 180-degree a tail wind coming over the stern, and 270-degree coming over the port beam.
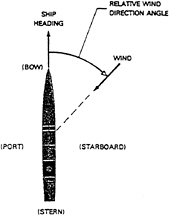
Fig. 3—Wind direction coordinate system.
Results and Discussion
Numerical results of the flow over a DD-963 ship configuration subject to an atmospheric wind speed of 15.44 m/s (30 knots) and a wind direction of 30 degrees are obtained. The flow condition yields a Reynolds number of 177 million based on the ship length for the full-scale ship. If the ship's beam is used for the Reynolds number basis, the above Reynolds number would have to be reduced approximately by a factor of 10. Whichever the way the Reynolds number is calculated, the flow falls into the turbulent flow range.
All the computations were performed on the Cray facilities at both NASA Ames Research Center and the DoD High Performance Computing facility at the Naval Ocean Center. Converged results were obtained in about 6,000 to 7,000 iterations (time

Fig. 4—Particle trace over DD-963 ship at even keel at 15.44 m/s (30 knots) and wind angle of 30 degrees from starboard. Perspective view.

Fig. 5—Particle trace over DD-963 ship at even keel at 15.44 m/s (30 knots) and wind angle of 30 degrees from starboard. Profile view.
steps) requiring approximately five hours of Cray C-90 CPU time. The large number of iterations is due to the very low freestream Mach number used in the compressible flow solver. The resulting CPU time is reasonable and affordable in today's environment of computer resources.
Particle Trace
Different views of particle trace of the streamlines emanating from various stations on the ship surface are shown in Figs.4 through 9 for three ship attitudes considered, namely ship at even keel, ship at 2-degree pitch bow down, and ship at 1-degree pitch and 5-degree roll. These figures all indicate that the flow is mostly separated, with free vortices originated from virtually all sections. There are two types of separation: one due to viscosity and the other due to sharp corners of the volume blocks representing the superstructure. The former is closely influenced by the types of flow involved which is Reynolds number dependent. The latter is purely an inviscid phenomenon, independent of the Reynolds number. Both types of separation create
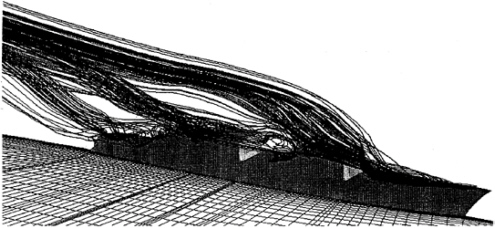
Fig. 8—Particle trace over DD-963 ship with 1-degree pitch and 5-degree roll at 15.44 m/s (30 knots) and wind angle of 30 degrees from starboard. Perspective view.

Fig. 9—Particle trace over DD-963 ship with 1-degree pitch and 5-degree roll at 15.44 m/s (30 knots) and wind angle of 30 degrees from starboard. Astern view.
free vortices as evidenced by streamlines rolling up forward and aft of the superstructure, on the flight deck, and aft of the stern. Figure 4 shows the perspective view of the particle trace and Fig.5 gives the profile view of the same airwake over the ship at even keel. The profile view helps indicate the actual height of the air burble (airwake) that might be misled by the perspective view. Of course the height, as well as the overall size, of the air burble grows as the flow proceeds downstream. The height can be twice as much as shown here in about three ship lengths away.
The size and shape of the air burble is directly affected by the aforementioned flow mechanisms. By comparing Figs.4, 6, and 8, it appears that the bow-down pitch of the ship makes instantaneous streamlines from all the region suppressed somewhat; the greater the pitch, the more the suppression. As a result, the ship pitched at two degrees (Fig.6) has an air burble thinner than that without pitch (Fig.4), and the thickness of the burble from the ship with 1-degree pitch yields an airwake size somewhere in between. Furthermore, since the 1-degree pitch attitude also includes a 5-degree roll, the instantaneous streamlines at the same time tend to hold down in the transverse direction, see Fig.8.
Figures 7 and 9 show the astern view of the particle trace of the ship attitudes at 2-degree pitch bow down and 1-degree pitch with 5-degree roll, respectively. Very complex flow patterns over the flight and missile decks are observed. Over the flight deck, except about one-third of the deck in the stern right corner where the flow is exposed to the freestream without influence of the hangar, much of the flow curves inboard and then upwards before proceeding aft. Free vortices are formed from viscous-vortex interactions which are characterized by massive flow separation. The inward flow from the port side might be caused in part by the crossflow reversal to be discussed later. The phenomena was also observed in wind tunnel measurements [5] as well as in the previous results [8] for the case of the ship at even keel.
Velocity Distribution
Figures 10 and 11 depict the contour of the velocity magnitude at the ship's center plane for cases of ship at even-keel attitude and pitched at two degrees bow down. In general, the velocity exhibits large deficiencies in the regions resembling the backward facing step, such as the mid-ship section aft of the forward superstructure, the flight deck aft of the hangar, the missile deck aft of the flight deck, and finally, the wake region aft of the stern. The flow in these region in fact can be characterized by that of a backward-facing step: massive flow separation involving reversed flow accompanied by circulation. In addition, there are two forward facing steps where the flow may have approached local stagnation. Outside the viscous region, the velocity recovers to the undisturbed stream at a height about half of the ship length.
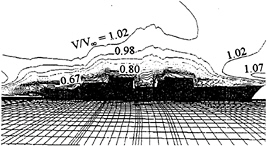
Fig. 10—Contour of resultant velocity along the center plane. Ship at even keel..
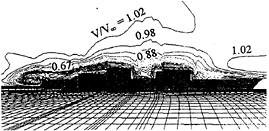
Fig. 11—Contour of resultant velocity along the center plane. Ship at 2-degree pitch bow down.
The effect of pitching is noted by increased local reversed flow regions for the pitched ship as compared to the ship without pitch. Also, values of local velocities in the separated flow regions generally are slightly lower in the pitched ship case.
The transverse velocity components for the three ship attitudes at a cross section passing through the bulls eye (the center of helicopter landing zone) are shown in Figs.12, 13, and 14, for cases of the even-keel ship, the ship with a two-degree bow-down pitch, and that with one-degree pitch and 5-degree roll, respectively. The negative values imply velocities follow the projected wind in the transverse direction, i.e., from starboard to port. The shear layer grows from the windward side (starboard side) to the leeward side (port side). Strictly speaking, however, the shear layer grows in both longitudinal and transverse directions, starting from the ship's bow. The sectional distributions help identify the crossflow reversal being significant as indicated by the positive values. These reversed crossflows are responsible for the inward instantaneous streamlines depicted in the particle trace.
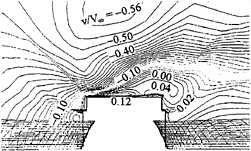
Fig. 12—Contour of transverse velocity over flight deck. Ship at even keel.
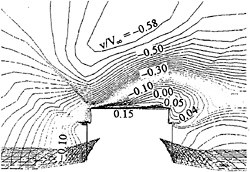
Fig. 13—Contour of transverse velocity over flight deck. Ship at 2-degree pitch bow down.
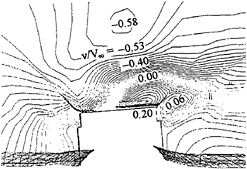
Fig. 14—Contour of transverse velocity over flight deck Ship at 1-deg pitch and 5-deg roll.
The pitch of the ship seems to have imposed little influence on the transverse velocity distribution as evidenced by remarkable similarity of the two contours, see Figs.12 and 13. However, the distribution is significantly altered by the rolling of the ship, see Fig.14. The crossflow reversal is postponed but further extended to the port side. Since the wind has a direction of 30 degrees from the starboard, the port side in fact serves as a backward-facing step for the transverse component flow. Geometrically, the rolling of the ship raises the height of the port side and therefore increases the size of the local separation region. It is noted that in Figs. 13 and 14 the water surface adjacent to the ship was inclined slightly in order to blend the water surface naturally with the ship hull.
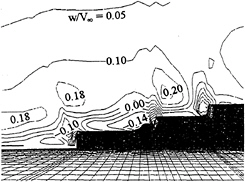
Fig. 15.—Contour of vertical velocity over flight and missile decks, Ship at even keel.
Figure 15 and 16 show the vertical velocity contours over the flight and missile decks for the ship at even keel and the ship pitched at two degrees bow down, respectively. Upward velocities are marked positive. The variation of vertical velocity, especially in the downward direction, is considerably larger in case of the pitched ship than that for the ship at even keel. The trend is consistent with the size of the local separated flow region observed in Figs.10 and 11.
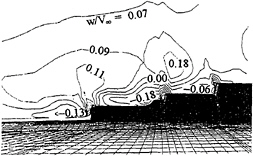
Fig. 16—Contour of vertical velocity over flight and missile decks, Ship at 2-deg pitch.
Mean Velocities along Flight Path
To evaluate the effect of ship pitch and roll on the helicopter landing operation, the mean velocities along the flight path directly aft the ship stern are examined. Having a 2.5-degree inclination with respect to the flight deck, the flight path starts more than one ship length away from the flight deck and ends at 5.91 meters (15 feet) above the bulls eye (center of flight deck), see Fig.17. The longitudinal, transverse, and vertical components of mean velocities along the flight path are shown in Figs.18, 19 and 20, respectively, from data with and without ship motion. The velocities are normalized by the freestream value and the distance is normalized by ship length.
Fig. 17—Geometry of the flight path having an inclination of 2.5 degrees
In general, the velocity decreases over the flight and missile decks because of the backward-facing-step type wake flow, as discussed previously. The magnitude of the longitudinal velocity is reduced by 50% at a point 5.91 meters above the bulls eye for ship at even keel. For a ship subject to pitch and/or roll, further drop in velocity is observed, see Fig.18. All three conditions yield an abrupt reduction in velocity right above the stern. This trend holds also for the transverse components if one considers their absolute values, ignoring the negative sign in Fig.19 which is merely an indication of direction. The effect of ship pitch and roll becomes noticeable about one ship length away from the bulls eye, and is significant about half of ship length away, and turns very severe within the ship's stern.
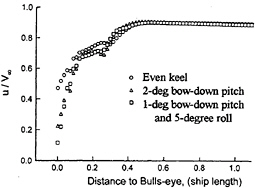
Fig. 18—Longitudinal velocities along flight path
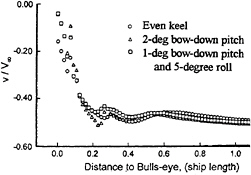
Fig. 19—Transverse velocities along flight path
For the vertical velocities, the variations are more drastic as shown in Fig.20. The magnitude of the vertical component varies as much as of 10% of the freestream value in both upward and downward direction. For ship at even keel, however, only positive w components are seen for this flight path. The effect of ship motion becomes noticeable about one ship length away from the bulls eye, and intensifies as it approaches the stern. The upward w component reaches its maximum above the stern, and then decrease continuously over the missile deck where it changes direction again. Above the flight deck, the viscous/vortex interaction becomes so intensive that no consistent trend can be found for this fluctuating velocity component.
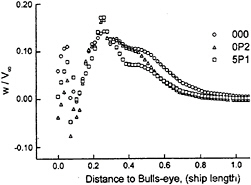
Fig. 20—Vertical velocities along flight path
Concluding Remarks
The airwake of a DD-963 ship configuration subject to atmospheric wind of 15.44 m/s (30 knots) at wind angle of 30 degrees is simulated by using a multi-zone, thin-layer Navier-Stokes method. The effect of ship motion is implemented by simulating the steady-state flowfield over the basic ship configuration that has pitched and/or rolled with respect to the water surface.
The resulting flow contains regions of massive flow separation along with free vortices. Major flow features including viscous-vortex interactions are captured. Some concluding remarks may be drawn:
-
The ship pitched bow down yields an air burble (airwake) thinner than that of a ship at even keel traveling at the same speed. Similarly, the ship rolled towards starboard results in a thinner air burble in the transverse direction.
-
The flow behind the superstructure or the hangar has characteristics of a backward-facing step with massive flow separation involving reversed flow accompanied by circulation. The pitched ship has larger local reversed flow regions than those of a ship at even keel.
-
The transverse velocity distribution seems to be little influenced by the pitch angle of the ship, but much affected by ship roll angle. On the other hand, the vertical velocities are significantly influenced by both pitch and roll angles.
Acknowledgment
The present work was supported by the Naval Air Warfare Center, Aircraft Division. The NASA Ames Research Center and DoD High Performance Computing facility provided the Cray CPU time.
References
1. Garnett, T.S. Jr., “Investifation to Study the Aerodynamic Ship Wake Turbulence Generated by a DD963 Destroyer,” Report No. NADC-77214–30, Boeing Vertol Company, Philadelphia, PA, Oct 1979.
2. Healey, J.V., “The Prospects for Simulating the Helicopter/Ship Interface,” Naval Engineers Journal, Vol. 99, No. 2, 1987. pp.45–63.
3. Carico, D., Reddy, W., DiMarzic, C., “Ship Airwake Measurement and Modeling Options for Rotorcraft Applications, ” AGARD Symposium on Aircraft Ship Operations, Paper 100, Seville, Spain, May 1991.
4. Blanc, T.V. and Larson, R.E., “Superstructure Flow Distortion Corrections for Wind Speed and Direction Measurements Made from NIMITZ Class (CVN68-CVN73) Ships,” NRL Report 9215, Naval Research Laboratory, Washington, DC, Oct 1989.
5. Healey, J.V., “The Airwake of a DD-963 Class Destroyer,” Naval Engineers Journal, Vol. 101, No. 2, 1989. pp. 36–42.
6. Healey, J.V., “A Data Base for Flight in the Wake of a Ship,” AIAA Paper 92–0295, Jan 1992.
7. Healey, J.V., “Wind Tunnel Datatape on DD-963 Class Destroyer,” Naval Post-Graduate School, Monterey, CA, 1990.
8. Tai, T.C. and Carico, D., “Simulation of DD-963 Ship Airwake by Navier-Stokes Method,” AIAA Paper 93–3002, July 1993 . Also Journal of Aircraft, Vol. 32, No. 6, 1995. pp. 1399–1401.
9. Tai, T.C., “Simulation of LPD Ship Airwake by Navier-Stokes Method,” Proceedings of the Sixth Asian Congress of Fluid Mechanics, Vol. II, May 1995, Singapore
10. Tai, T.C., “A Single Structured Grid for Complex Ship Geometry,” in Numerical Grid Generation in Computational Fluid Dynamics and Related Fields, Edited by N.P.Weatherill, Pineridge Press Limited, Swansea, U.K. 1994.
11. Sorenson, R.L., “The 3DGRAPE Book: Theory, Users' Manual, Examples,” NASA Technical Memorandum 102224, July 1989.
12. Volpe, G., “On the Use and Accuracy of Compressible Flow Codes at Low Mach Numbers, ” AIAA Paper 91–1662, presented at AIAA 22nd Fluid Dynamics, Plasma Dynamics & Lasers Conference, Honolulu, HI, June 1991.
13. Thomas, J.L., Krist, S.T., and Anderson, W.K., “Navier-Stokes Computations of Vortical Flows over Low-Aspect-Ratio Wings,” AIAA Journal, Vol. 28, No. 2, 1990. pp. 205–212.
14. Baldwin, B.S., and Lomax, H., “Thin-Layer Approximation and Algebraic Model for Separated Turbulent Flows,” AIAA Paper 78–0257, Jan 1978.
15. Baldwin, B. and Barth, T., “A One-Equation Turbulent Transport Model for High Reynolds Number Wall-Bounded Flows,” NASA TM-102847, 1990.
16. Spalart, P., and Allmaras, S., “A One-Equation Turbulence Model for Aerodynamic Flows,” AIAA Paper 92–0439, Jan 1992.
17. Rumsey, C.L., and Vatsa, V.N., “A comparison of the Predictive Capabilities of Several Turbulence Models Using Upwind and Central-Difference Computer Codes,” AIAA Paper 93–0192, Reno, NV, Jan 1993.
18. Degani, D., and Schiff, L.B., “Computation of Supersonic Viscous Flows Around Pointed Bodies at Large Incidence,” AIAA Paper 83–0034, 1983.
19. Plate, E.J., Engineering Meteorology, Elsevier Scientific Publishing Co., Amsterdam, 1982, pp. 527–569.













