Freak Waves—A Three-Dimensional Wave Simulation
K.Trulsen, K.Dysthe (University of Bergen, Norway)
Abstract
We seek to understand the occurrence of so-called freak waves, extremely large and steep ocean surface waves. Our basic assumption is that these waves can be produced by nonlinear self modulation of a slowly modulated wave train. A field experimental record of a freak wave event is presented, and is shown to comply with a description as a weakly nonlinear band-limited process. However, existing models for weakly nonlinear, slowly modulated surface gravity waves, i.e. the third order nonlinear Schrödinger equation and the fourth order modified nonlinear Schrödinger equation, do not have sufficient resolution in bandwidth. We thus extend the modified nonlinear Schrödinger equation by relaxing the narrow bandwidth constraint to make it more suitable for application to a realistic ocean wave spectrum. A split-step Fourier collocation method is discussed for the numerical solution of the new equation.
1
Introduction
The sudden occurrence of extremely large and steep ocean waves imposes a hazard to fishing boats, ships and off-shore oil activities. It is therefore important to understand the mechanisms that can give rise to such waves.
The term “freak wave” was apparently introduced by Draper (1965). It has been used to denote single waves that are extremely “unlikely” as judged by a Rayleigh distribution of waveheights (Dean 1990). In practical terms, a waveheight H exceeding the significant waveheight H1/3 by a factor 2.2 has been applied as a criterion. Extreme waves occurring in laboratory generated irregular wavetrains have been found to possess a significant crest-to-trough asymmetry (Stansberg 1990). A ratio between the maximum crest height and the associated peak-to-trough height H in the range 0.6–0.65 is not unusual.
One can often explain frequent events of extreme waves at certain geographical locations by the presence of ocean currents or bottom topography that can cause wave energy to focus in a small area due to refraction, reflection (caustics) and wave trapping. A well known locality with frequent reports of dangerous waves is the area off the east coast of South Africa, where the Agulhas current runs southwest along the coast and meets swells from storms farther south. Many ships have been lost due to unusually high waves in this area (Mallory 1974). These mechanisms are well understood, and can essentially be explained by linear theory.
It is, however, not well understood why exceptionally large waves can occur in the open ocean, away from non-uniform currents or bathymetry.
Field measurements of such an event are presented in figures 1 and 2. Figure 1 shows a time series of the water surface elevation at one particular point. The measurements were taken by a downward pointing radar at 16/11-E in the Norwegian sector of the North Sea on January 1, 1995. We see a high wave occurring approximately four and a half minutes after the beginning of the time series. From these data we compute the significant waveheight (crest-to-trough) to be 10.8 m, while the maximum waveheight is 25.6 m (we have defined crests/troughs as the maxima/minima of the time series between zero crossings, sometimes referred to as z-crests and z-troughs). With the ratio 2.36 between the maximum height and the significant height, this wave qualifies as a freak wave according to the above definitions. The corresponding power spectrum is shown in figure 2. Unfortunately, no measurements on the direc
tional spread of the wave spectrum is available at the same location for this event.
The field measurements presented in figures 1 and 2 can be used to get a rough quantitative idea of the magnitudes of some relevant parameters characterizing these waves. We will describe the wavetrain as a slow modulation around a central wave (with wave vector k0) of the energy spectrum. The central frequency can be estimated from figure 2 to be f0 ≈ 0.074 Hz. The depth at 16/11-E is h ≈ 70 m, and the bottom is virtually horizontal in a large neighborhood of this site. The dispersion relation for gravity waves on finite depth is
ω2=gk tanh kh, (1)
where ω = 2πf and g = 9.8 m/s2. The central wavenumber can be estimated as k0 ≈ 0.024 m–1, and the normalized inverse depth is (k0h)–1 ≈ 0.60. The wave amplitude is seen to be about a ≈ 5 m, and the central wave steepness is therefore of the order k0a ≈ 0.12.
The deviation in frequency (half the width of the “top” of the spectrum) associated with the slow modulation can be estimated to be Δf ≈ 0.018 Hz. As an estimate for frequency bandwidth we therefore have Δf/f0 ≈ 0.24. An estimate of the wavenumber bandwidth in the direction of the central wave vector can then be obtained by substituting
ω = ω0 ± Δω and k = k0 ± Δk|| (2)
into the dispersion relation (1). To linear order in the bandwidths one has
(3)
The factor multiplying the frequency bandwidth is 2 for deep water and decreases to unity for decreasing depth. In our case (3) provides the estimate for the wavenumber bandwidth along the direction of the central wave vector Δk||/k0 ≈ 0.40.
The time series in figure 1 cannot give information on the directional spread in the two horizontal dimensions. However, these wind-driven wave systems typically have angular deviations between 20° and 30°. This gives ![]() .
.
We seek to explain the occurrence of freak waves in the absence of ocean currents or non-uniform bottom topography by nonlinear self modulation of a wave train. Even though the wind is essential to produce the wave spectrum, it can be neglected over the relatively short scales characteristic for a freak wave event. The directional spread of the spectrum is assumed to be important and a three-dimensional model must therefore be employed.
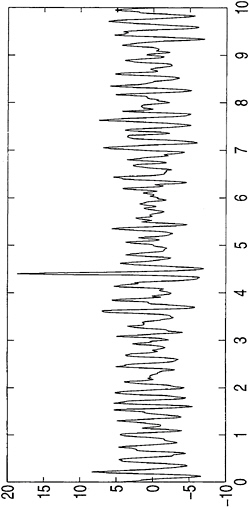
Figure 1: Ten minute wave elevation time series measured by a downward pointing radar at 16/11-E in the Norwegian sector of the North Sea. First axis is time in minutes, second axis is elevation n in meters. Data courtesy of J.I.Dalane and O.T.Gudmestad of Statoil.
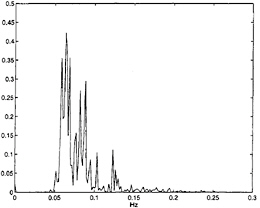
Figure 2: Power spectrum for the time series in figure 1. The frequency is given in Hertz. Data courtesy of J.I.Dalane and O.T.Gudmestad of Statoil.
Theoretical models describing the slow space and time evolution of weakly nonlinear surface gravity waves are generally based on the two assumptions: that the steepness is small k0a ![]() 1, and that the bandwidth is narrow |Δk|/k0
1, and that the bandwidth is narrow |Δk|/k0![]() 1. Typically, one assumes that the steepness and the bandwidth are of the same order of magnitude
1. Typically, one assumes that the steepness and the bandwidth are of the same order of magnitude ![]() such that the leading nonlinear and dispersive effects balance at the third order
such that the leading nonlinear and dispersive effects balance at the third order ![]() The resulting amplitude modulation equation is known as the nonlinear Schrödinger equation (NLS). This equation was pioneered by Benney & Newell (1967) for nonlinear dispersive waves in general, by Zakharov (1968), Hasimoto & Ono (1972) and Davey (1972) for gravity waves on deep water, and by Benney & Roskes (1969) for gravity waves on finite depth. A modification of the nonlinear Schrödinger equation to fourth-order accuracy
The resulting amplitude modulation equation is known as the nonlinear Schrödinger equation (NLS). This equation was pioneered by Benney & Newell (1967) for nonlinear dispersive waves in general, by Zakharov (1968), Hasimoto & Ono (1972) and Davey (1972) for gravity waves on deep water, and by Benney & Roskes (1969) for gravity waves on finite depth. A modification of the nonlinear Schrödinger equation to fourth-order accuracy ![]() which we shall denote the MNLS equation, was derived by Dysthe (1979) for gravity waves on infinite depth, with minor modifications for gravity waves on deep water by Lo & Mei (1985), and by Brinch-Nielsen & Jonsson (1986) for gravity waves on finite depth. We here define finite depth, deep water and infinite depth as (k0h)–1 being
which we shall denote the MNLS equation, was derived by Dysthe (1979) for gravity waves on infinite depth, with minor modifications for gravity waves on deep water by Lo & Mei (1985), and by Brinch-Nielsen & Jonsson (1986) for gravity waves on finite depth. We here define finite depth, deep water and infinite depth as (k0h)–1 being ![]() and 0, respectively.
and 0, respectively.
The MNLS equation has successfully been used to model several aspects of the long-time evolution of weakly nonlinear narrow-banded water waves. It predicts the asymmetric growth of upper and lower sidebands, accompanied by the forward steepening of initially symmetric wave-groups as reported in the experiment of Feir (1967). Enhanced with a highly simplified model for wave damping due to breaking, it was shown by Trulsen & Dysthe (1990) that the MNLS equation can predict the permanent downshift of the carrier wave frequency, which was observed experimentally by Lake et al. (1977). Furthermore, with the additional enhancement of a model for wind growth due to Plant (1982) and damping by wave breaking, it was shown by Trulsen & Dysthe (1992) that the MNLS equation can also predict that a strong wind can stabilize Stokes waves such that modulational instability and frequency downshift are suppressed. This was observed experimentally by Bliven et al. (1986). The MNLS equation was employed by Hara & Mei (1991) to predict downshift of the carrier wave frequency for waves forced by a weak wind and damped by eddy viscosity. There has also been recent work further investigating the downshift by the addition of damping terms to the MNLS equation (e.g. Uchiyama & Kawahara 1994; Kato & Oikawa 1995). These applications all consider evolution in one horizontal dimension.
For application of the MNLS equation to describe the situation in figures 1 and 2, we observe that the central wave steepness is within the domain of validity of the MNLS equation, but the bandwidth is not. Therefore, an improved model is called for that can describe broader bandwidth wave trains. To this end the Zakharov integral equation (Zakharov 1968; Crawford, Saffman & Yuen 1980; Stiassnie & Shemer 1984) has been developed to avoid the limitation in bandwidth altogether. This additional generality has the price of making the Zakharov equation unnecessarily expensive to solve numerically for the present problem. In order to maintain the relative simplicity of the MNLS equation, it is desirable to look for ways to relax the bandwidth constraint, while keeping the same accuracy in nonlinearity.
Even though the waves in figure 1 are not on deep water, we limit the present discussion to waves on deep water. In section 2 we first review the NLS and MNLS equations, and then summarize a new modified nonlinear Schrödinger equation for broader bandwidths by requiring ![]() while keeping the same accuracy in nonlinearity (Trulsen & Dysthe 1996). The new equation will be denoted the BMNLS equation. The resolution in bandwidth can be assessed by comparison between predicted and exact stability results for Stokes waves, and the new equation has been found to be in good conformance with the resolution required by the above order-of-magnitude analysis. An extension to finite depth has been derived by us, and will be reported in the future.
while keeping the same accuracy in nonlinearity (Trulsen & Dysthe 1996). The new equation will be denoted the BMNLS equation. The resolution in bandwidth can be assessed by comparison between predicted and exact stability results for Stokes waves, and the new equation has been found to be in good conformance with the resolution required by the above order-of-magnitude analysis. An extension to finite depth has been derived by us, and will be reported in the future.
The BMNLS equation can be solved numerically with periodic boundary conditions in two hor
izontal dimensions by a split-step Fourier collocation method. This method has been successfully used to solve the MNLS equation in one horizontal dimension by Lo & Mei (1985) and Trulsen & Dysthe (1990, 1992), and in two horizontal dimensions by Lo & Mei (1987). The NLS equation has been found to be unsuitable for computations of the evolution of a Stokes wave in two horizontal dimensions (Martin & Yuen 1980) because the unboundedness of the region of instability of Stokes waves in the Δk plane can cause energy to be leaked to high spectral components. Lo & Mei (1987) found that this energy leakage was suppressed by the higher-order corrections of the MNLS equation. In section 4 we review the numerical method for application to the BMNLS equation.
Experiments (Stansberg 1990) have shown that extreme waves (H ≤ 2H1/3) may also occur for essentially two-dimensional waves. Yasuda et al. (1992) have made two-dimensional simulations based on a method of Dommermuth & Yue (1987). They claim to see freak events that are similar to those observed in nature. Further two-dimensional computations have been carried out by Baldock & Swan (1994) and Taylor & Haagsma (1994) based on Fourier expansion of the potential flow equations.
We believe that three-dimensional wave modulation is important and plan to use the BMNLS equation to carry out fully three-dimensional computations of a spectrum that is statistically stationary and homogeneous, similar to the energetic part of a realistic ocean wave spectrum. Our interests include the occurrence, parametric dependence and dynamics of freak waves. This work is underway and will be reported in the future. Preliminary numerical results are briefly discussed in section 5, revealing that evolution in two and three dimensions are qualitatively different
2
Evolution equations for narrow-banded irregular waves on deep water
We start with the equations for the velocity potential ![]() (t, x, z) and surface displacement ζ(t, x) of an incompressible fluid with uniform depth h,
(t, x, z) and surface displacement ζ(t, x) of an incompressible fluid with uniform depth h,
![]() 2
2![]() =0 for –h<z<ζ, (4)
=0 for –h<z<ζ, (4)
with the surface conditions at z=ζ
(5)
(6)
and the bottom condition
(7)
The horizontal position vector is x=(x,y), the vertical coordinate is z, and ![]()
Subject to the assumptions
(8)
we employ the harmonic expansions of the velocity potential and surface displacement,
(9)
(10)
where c.c. denotes the complex conjugate, and the phase is θ=k0x–ω0t for a wave with central wave vector in the x-direction. The slow drift ![]() and set-down
and set-down ![]() as well as the harmonic amplitudes A, A2,…, B, B2,…are functions of the slow modulation variables
as well as the harmonic amplitudes A, A2,…, B, B2,…are functions of the slow modulation variables ![]() x and t. Additionally,
x and t. Additionally, ![]()
![]() depends on the slow vertical variable
depends on the slow vertical variable ![]() z, while A, A2,…depend on the basic vertical coordinate z.
z, while A, A2,…depend on the basic vertical coordinate z.
The leading-order perturbation problem for the first harmonic simply requires that the dispersion relation for deep-water gravity waves must be satisfied
(11)
In the following, results have been made dimensionless by the substitutions
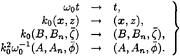
(12)
Hence, the ordering parameter ![]() is implied in the variables, but does not appear explicitly.
is implied in the variables, but does not appear explicitly.
At the third order ![]() the celebrated nonlinear Schrödinger equation is obtained for the slow evolution of A
the celebrated nonlinear Schrödinger equation is obtained for the slow evolution of A
(13)
At the fourth order ![]() we get the coupled evolution equations for A and
we get the coupled evolution equations for A and ![]() known as the modified nonlinear Schrödinger equation,
known as the modified nonlinear Schrödinger equation,
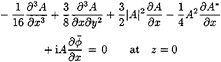
(14)
(15)
(16)
(17)
In order to improve the resolution in bandwidth, we employ the new assumptions on the dimensional variables
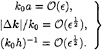
(18)
The previous harmonic expansions of the velocity potential (9) and surface displacement (10) can still be used, but now ![]() A,A2,…,B,B2,…are functions of the new slightly faster modulation variables
A,A2,…,B,B2,…are functions of the new slightly faster modulation variables ![]() and
and ![]() Additionally,
Additionally, ![]() now depends on the new slightly faster vertical variable
now depends on the new slightly faster vertical variable ![]()
We insist on keeping the same accuracy in nonlinearity as in the MNLS equation. Since none of the fourth-order contributions here are fourth-order nonlinear, it suffices to consider the new equation only up to order ![]() Carrying the perturbation analysis through in a similar fashion, the coupled evolution equations for A and
Carrying the perturbation analysis through in a similar fashion, the coupled evolution equations for A and ![]() now become
now become
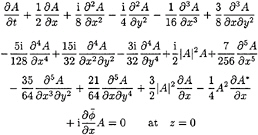
(19)
(20)
(21)
(22)
The surface displacement is expressed by (10),
where
(23)
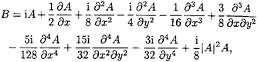
(24)
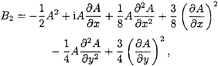
(25)
and
(26)
For numerical solution of the governing equations it is convenient to transform into a moving coordinate system to eliminate the leading order advection with the group velocity of the central wavenumber ![]() Hence we may introduce the transformations
Hence we may introduce the transformations
x–cgt=ξ and t=τ, (27)
where τ is a slow evolution time coordinate.
It has been found advantageous to use the different moving transformation (Lo & Mei 1985)
x/cg–t=ξ and x=η, (28)
where η is a slow evolution space coordinate measuring the fetch. The faster coordinate ξ is now the negative time seen by a stationary observer.
3
Stability of Stokes waves
The three evolution equations presented herein (NLS, MNLS and BMNLS) all have the uniform Stokes wave as an exact solution. It is given by
(29)
The surface displacement can then be expressed as
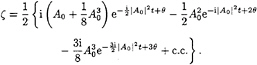
(30)
Upon making the substitutions ![]() and
and ![]() we recover the familiar form of the Stokes wave expansion accurate to the third order
we recover the familiar form of the Stokes wave expansion accurate to the third order
(31)
The stability of the Stokes wave can be investigated by assuming small perturbations in amplitude and phase of the form
(32)
now with A0 real, having the plane wave solution
(33)
The linear dispersion relation for this perturbation for the NLS equation is given by
(34)
while for the MNLS and BMNLS equations we have
(35)
where
(36)
(37)
for the MNLS equation, while
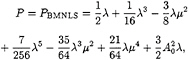
(38)
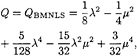
(39)
for the BMNLS equation, and where
(40)
Stokes waves are not representative of realistic ocean waves like those shown in figure 1. However, the enhanced resolution in bandwidth of the BMNLS equation can conveniently be assessed by comparing the predicted instability of Stokes waves with exact results. Such detailed comparisons are presented in Trulsen & Dysthe (1996). The new equation has been found to have good resolution in bandwidth for the characteristic steepness and bandwidths discussed in the introduction.
In figure 3 we show the characteristic shapes of the unstable domains in the (λ, µ) plane for the three evolution equations when A0=0.12. The NLS equation has an unbounded instability region with most unstable perturbations continuously distributed along the hyperbola ![]() The higher-order modified nonlinear Schrödinger equations have primary instability regions that are bounded, and they have the most unstable perturbations located at isolated points near the origin. The BMNLS equation confines the instability region even better than the MNLS equation. This confinement of the instability region resolves the problem of energy leakage reported by Marin & Yuen (1980) for numerical computations with the NLS equation.
The higher-order modified nonlinear Schrödinger equations have primary instability regions that are bounded, and they have the most unstable perturbations located at isolated points near the origin. The BMNLS equation confines the instability region even better than the MNLS equation. This confinement of the instability region resolves the problem of energy leakage reported by Marin & Yuen (1980) for numerical computations with the NLS equation.
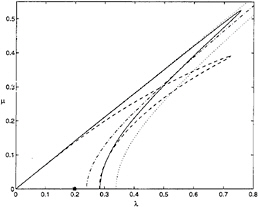
Figure 3: Instability regions for A0=0.12: – –, BMNLS; —, MNLS; ···, NLS. Most unstable perturbation: *, BMNLS; ○, MNLS; – ·, NLS.
4
Numerical method
The split-step Fourier collocation method previously used by Lo & Mei (1985, 1987) and Trulsen & Dysthe (1990, 1992) for the MNLS equation has been implemented for the BMNLS equation. The method is briefly reviewed here.
The governing equations for A (subject to the transformation (27) can be written in the form
(41)
where L is a linear spatial differential operator and N is a nonlinear function of A.
The solution is assumed to be periodic in ξ and y. If we let both periods be 2π, the discrete Fourier transform of A is defined as
(42)
where ξm=2πm/M and yn=2πn/N.
The linear part LA is characterized by high-order spatial derivatives, which normally suggests that the time-step must be small to maintain numerical stability. The linear differential equation
(43)
can be solved exactly and efficiently in Fourier space by multiplication of each Fourier mode by a constant,
(44)
The nonlinear part N (A) contains no higher than first derivatives, and the nonlinear equation
(45)
can be solved by an explicit one-step scheme in physical space. A numerical solution for (41) can therefore be obtained by a split-step method where the linear and nonlinear parts are alternately solved in Fourier and physical space. The order of accuracy of this scheme is limited by the fact that the linear and nonlinear operators do not commute. Thus with the iteration…NL…the method is first order accurate provided the integration scheme for (45) is at least first order accurate. With the iteration…NLLN… the method is second order accurate provided the integration scheme for (45) is at least second order accurate.
5
Preliminary numerical results
We here briefly mention some preliminary results on the evolution of a wave spectrum in two and three dimensions.
It is well known that the two-dimensional conservative evolution of a Stokes wave according to the NLS, MNLS and Zakharov integral equations exhibit cyclical modulation and demodulation (recurrence) provided the Stokes wave has been perturbed on few of its unstable sidebands. If the Stokes wave has been perturbed on several unstable sidebands, the simple cyclical behavior disappears, and the evolution becomes more complicated. The peak frequency in the wave spectrum can be temporarily upshifted and downshifted, but there is no tendency of a permanent shift. It is generally assumed that the frequency downshift observed in long wave tanks (Lake et al. 1977) is due to dissipation and wave breaking (Trulsen & Dysthe 1990; Tulin 1996).
The three-dimensional evolution of waves has so far not been extensively studied. It is worthwhile to notice that in the experiment of Lake et al. (1977) where the downshift was first reported, the wave tank was three times wider than the central wavelength. Other experiments reporting downshift have also used wide tanks. Narrow-banded oblique sideband modulation is therefore possible, and can be investigated with the BMNLS equation. From our numerical computations, we find that the conservative evolution in three dimensions is qualitatively different from that in two dimensions: The peak frequency in the wave spectrum can be permanently downshifted (for the duration of the numerical computation). We intend to published these results elsewhere.
6
Conclusion
We seek to understand the occurrence of freak waves by nonlinear self modulation of a slowly modulated weakly nonlinear wave train, for which ocean currents or non-uniform bottom topography can be neglected. Field observations have been presented, suggesting that the wave conditions leading to freak waves can be described as a narrow-banded weakly nonlinear wave train. However, the required bandwidth is wider than the constraints imposed by the existing fourth order modified nonlinear Schrödinger equation of Dysthe (1979).
We have derived a new modified nonlinear Schrödinger equation valid for broader bandwidths, which is more appropriate for a realistic ocean wave spectrum. This paper is limited to a discussion of the new broader bandwidth equation for deep water, and a description of a numerical method for its solution.
Preliminary numerical results indicate that the evolution of a wave spectrum in two and three dimensions are qualitatively different.
Extension of the modified nonlinear Schrödinger equation for finite depth to broader bandwidth is necessary to properly deal with the field measurements presented above.
Stimulating discussions with Dr. Anne Karin Magnusson of The Norwegian Meteorological Institute (DNMI/Bergen) are gratefully acknowledged. We thank J.I.Dalane and O.T.Gudmestad of Statoil for providing the field experimental data. This research has been supported by the Norwegian Research Council through a post doctoral fellowship (NFR 109328/410) and a grant for computing time (Programme for Supercomputing).
References
[1] Baldock, T.E. & Swan, C. ( 1994). Numerical calculations of large transient water waves. Appl. Ocean Res., 16, 101–112.
[2] Benney, D.J. & Newell, A.C. ( 1967). The propagation of nonlinear wave envelopes. J. Math. Phys., 46, 133–139.
[3] Benney, D.J. & Roskes, G.J. ( 1969). Wave instabilities. Studies Appl. Math, 48, 377–385.
[4] Bliven, L.F., Huang, N.E., & Long, S.R. ( 1986). Experimental study of the influence of wind on Benjamin-Feir sideband instability. J. Fluid Mech., 162, 273–260.
[5] Brinch-Nielsen, U. & Jonsson, I.G. ( 1986). Fourth order evolution equations and stability analysis for Stokes waves on arbitrary water depth. Wave Motion, 8, 455–472.
[6] Crawford, D.R., Saffman, P.G., & Yuen, H.C. ( 1980). Evolution of a random inhomogeneous field of nonlinear deep-water gravity waves. Wave Motion, 2, 1–16.
[7] Davey, A. ( 1972). The propagation of a weak nonlinear wave. J. Fluid Mech., 53, 769–781.
[8] Dean, R.G. ( 1990). Freak waves: A possible explanation. In A.Tørum & O.T.Gudmestad (Eds.), Water Wave Kinematics (pp. 609–612): Kluwer.
[9] Dommermuth, D.G. & Yue, D.K.P. ( 1987). A high-order spectral method for the study of nonlinear gravity waves . J. Fluid Mech., 184, 267–288.
[10] Draper, L. ( 1965). ‘Freak' ocean waves. Marine Observer, 35, 193–195.
[11] Dysthe, K.B. ( 1979). Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. A, 369, 105–114.
[12] Feir, J.E. ( 1967). Discussion: some results from wave pulse experiments. Proc. R. Soc. Lond. A, 299, 54–58.
[13] Hara, T. & Mei, C.C. ( 1991). Frequency downshift in narrowbanded surface waves under the influence of wind. J. Fluid Mech., 230, 429–477.
[14] Hasimoto, H. & Ono, H. ( 1972). Nonlinear modulation of gravity waves. J. Phys. Soc. Japan, 33, 805–811.
[15] Kato, Y. & Oikawa, M. ( 1995). Wave number downshift in modulated wavetrain through a nonlinear damping effect. J. Phys. Soc. Japan, 64, 4660–4669.
[16] Lake, B.M., Yuen, H.C., Rungaldier, H., & Ferguson, W.E. ( 1977). Nonlinear deep-water waves: theory and experiment. Part 2: Evolution of a continuous wave train. J. Fluid Mech., 83, 49–74.
[17] Lo, E. & Mei, C.C. ( 1985). A numerical study of water-wave modulation based on a higher-order nonlinear Schrödinger equation. J. Fluid Mech., 150, 395–416.
[18] Lo, E.Y. & Mei, C.C. ( 1987). Slow evolution of nonlinear deep water waves in two horizontal directions: A numerical study. Wave Motion, 9, 245–259.
[19] Mallory, J.K. ( 1974). Abnormal waves on the south east coast of South Africa. Int. Hydrog. Rev., 51, 99–129.
[20] Martin, D.U. & Yuen, H.C. ( 1980). Quasi-recurring energy leakage in the two-space-dimensional nonlinear Schrödinger equation. Phys. Fluids, 23, 881–883.
[21] Plant, W.J. ( 1982). A relationship between wind stress and wave slope. J. Geophys. Res., 87, 1961– 1967.
[22] Stansberg, C.T. ( 1990). Extreme waves in laboratory generated irregular wave trains. In A. Tørum & O.T.Gudmestad (Eds.), Water Wave Kinematics (pp. 573–589): Kluwer.
[23] Stiassnie, M. & Shemer, L. ( 1984). On modifications of the Zakharov equation for surface gravity waves . J. Fluid Mech., 143, 47–67.
[24] Taylor, P.H. & Haagsma, I.J. ( 1994). Focussing of steep wave groups on deep water. In Waves— Physical and Numerical Modelling.
[25] Trulsen, K. & Dysthe, K.B. ( 1990). Frequency down-shift through self modulation and breaking. In A.Tørum & O.T.Gudmestad (Eds.), Water Wave Kinematics (pp. 561–572): Kluwer.
[26] Trulsen, K. & Dysthe, K.B. ( 1992). Action of windstress and breaking on the evolution of a wavetrain . In M.L.Banner & R.H.J.Grimshaw (Eds.), Breaking Waves (pp. 243–249): Springer.
[27] Trulsen, K. & Dysthe, K.B. (In press 1996). A modified nonlinear Schrödinger equation for
broader bandwidth gravity waves on deep water. Wave Motion.
[28] Tulin, M.P. ( 1996). Breaking of ocean waves and downshifting . In J.Grue, B.Gjevik, & J.E. Weber (Eds.), Waves and Nonlinear Processes in Hydrodynamics (pp. 177–190): Kluwer.
[29] Uchiyama, Y. & Kawahara, T. ( 1994). A possible mechanism for frequency down-shift in nonlinear wave modulation . Wave Motion, 20, 99–110.
[30] Yasuda, T., Mori, N., & Ito, K. ( 1992). Freak waves in unidirectional wave trains and their properties. In Proc. 23rd Int. Conf. on Coastal Engineering.
[31] Zakharov, V.E. ( 1968). Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys., 9, 190–194.
DISCUSSION
C.T.Stansberg
Norwegian Marine Technology Research Institute, Norway
The paper presents an interesting approach for extending the Modified Nonlinear Schrodinger Equation (MNLS), previously developed for weakly nonlinear, narrow-banded deep-water waves, to more broad-banded spectral conditions. The principles and procedures of the approach are described, while final numerical simulations have not yet been carried out. In the future, further development including finite water depths and multidirectional waves are also planned. By this, the authors seek to explain the occurrence of extraordinarily large (“freak”) wave events observed in the real ocean. The work is based on previous works by the same authors, demonstrating the performance of the existing MNLS model for slowly varying envelope waves. This model is believed to work quite well for such waves, in fact recent experiments on bichromatic deep-water unidirectional waves in a long channel (Stansberg 1995) have further confirmed its validity.
The question is whether the same model is capable of explaining extreme waves occurring in the full-scale conditions presented in Figures 1 & 2. It will therefore be quite interesting to see the forth-coming results from the simulations. I have some comments to this problem, based on recent experimental results:
-
One has reason to believe that increased spectral bandwidth as well as multidirectionality will reduce the growth of nonlinear self-modulations. This has, for example, been experimentally demonstrated in Standsberg (1994), where these effects have been systematically investigated. It may possibly be explained by the reduced “lifetime” of wave groups. Other recent experiments (not yet published) also indicate that self-modulation instabilities are less pronounced in finite water conditions, which may be due to change of the dispersion relation as well as the increasing presence of other bottom-induced processes. As a result, we can raise the following questions:
-
How dominating will the self-modulation instability effects be relative to other physical processes in the full scale wave condition presented in the paper? And if the extreme event in Figure 1 is due to such self-modulation effects, what is its statistical significance?
Although the complete answering of these questions is probably far ahead, the forth-coming simulation work announced in the paper will be valuable contributions on the subject, and are being looked forward to.
REFERENCES
Stansberg, C.T. ( 1994), “Effects from Directionality and Spectral Bandwidth on Non-Linear Spatial Modulations of Deep-Water Surface Gravity Waves”, in Proceedings, Vol. 1. the 24th International Conference on Coastal Engineering (Ed.: B.Edge), held in Kobe, Japan, October 1994 (Proceedings published by ASCE in 1995) , pp. 579–593.
Stansberg, C.T. ( 1995), “Spatially Developing Instabilities Observed in Experimental Bichromatic Wave Trains”, in Proceedings, Vol. 3, the 26th IAHR Congress (HYDRA 2000), London, September 1995, pp. 180–185.
DISCUSSION
O.T.Gudmestad
STATOIL, Norway
The development of the fourth order modified nonlinear Schrodinger equation for narrow banded deep water waves [Dysthe, 1979] represented an important contribution to the understanding of non-linear waves. This paper has been much referred to in the literature. The present modification for a relaxed narrow bandwidth constraint is very much welcome and contributes to further understanding of nonlinear wave processes in deep waters.
The offshore industry is at present very interested in obtaining detailed knowledge about wave processes in steep waves as these contribute to transient higher order loading of slender structures (Stansberg and Gudmestad, 1996). Given a more exact description of the velocity potential as obtained by Trulsen and Dysthe, it will be possible to obtain more exact values for velocity and acceleration terms whereby the loading can be estimated with higher accuracy also in steep waves. The industry is looking forward to the continuation of this promising research.
REFERENCES
Dysthe, K.B. ( 1979). “Note on a modification of the nonlinear Schrodinger equation for application to deep water wave,” Proc. R. Soc. London A, 369, 105–114.
Stansberg, C.T. and Gudmestad, O.T. ( 1996). “Nonlinear random wave kinematics models verified against measurements in steep waves,” Proc. OMAE 96, Firenze, June 1996.
AUTHORS' REPLY
According to the theoretical work of Alber (1978), the self-modulational instability disappears when the spectral bandwidth (σ) exceeds a critical value that is proportional to the mean square slope ![]() His stability criterion seems to be satisfied in most sea conditions. The absence of the self-modulation instability does not mean that nonlinear interactions are unimportant.
His stability criterion seems to be satisfied in most sea conditions. The absence of the self-modulation instability does not mean that nonlinear interactions are unimportant.
In the spectral regime, they are at least partly responsible for the downshift of the spectral peak. That is a slow statistical effect described by the Hasselman type interaction integral. Only when the spectral bandwidth is small (subcritical in Alber's sense) can a rapid downshift take place, as demonstrated by us.
In the spatial regime, the nonlinear interaction may have unexpected effects yet to be explored.
REFERENCE
Alber, I.E. ( 1978). “The effects of randomness on the stability of two-dimensional surface wavetrains,” Proc. R. Soc. Lond. A, 363, pp. 525–546.











