The Wake of a Bluff Body Moving Through Waves
R.Arkell, J.Graham (Imperial College, United Kingdom)
Abstract
This paper describes a numerical simulation of the development of a vortex street wake behind a bluff body when subject to a disturbance field induced by free surface waves. The geometry studied in the present case is of a long vertical surface piercing circular cylinder moving steadily parallel to the direction of propagation of the waves.
In the first part of the study, the flow field is simulated at low Reynolds numbers and assuming locally two dimensional flow. The numerical simulation is based on a vortex (particle) method which includes the effect of viscous diffusion and accurately simulates the time dependent Navier-Stokes equations, which are solved in stream function-vorticity form to compute the velocity and diffusion fields. Comparisons are presented between the numerical simulations and flow visualisations at similar Reynolds numbers and wave-cylinder conditions obtained in towed cylinder experiments in a wave tank using dye.
In the second part, three-dimensional numerical flow simulations are carried out using an unsteady Navier-Stokes code based on convection of vortons. Results for a vertical cylinder translating through waves and a tapered cylinder in uniform translation are presented.
1
Introduction
The fundamental problem of the persistence of the wake of a moving body is an interesting one: wakes of ships are observed to persist for tens of kilometers on the surface of the sea under the right conditions. Frictional forces within the fluid tend to reduce the velocity defect in the wake rapidly, and diffuse vorticity causing the wake to spread in a lateral sense (where gradients of vorticity are largest). The effects on the wake decay of parameters which include body shape, local Reynolds number, free surface conditions, and background turbulence are not yet fully understood.
The work reported here is an investigation into the effect of free surface waves on the vortex shedding and subsequent development of the wake of a vertical cylinder translating steadily under conditions such that the forward speed exceeds that of the particle orbital speed of the wave-induced local velocity field. A reversing incident flow relative to the cylinder is therefore not normally present, and the wave field represents a perturbation to the uniform incident flow. The vast majority of bluff body studies have focused on the effects of either a steady incident flow or of oscillatory incident flow on circular cylinders. Some have included the combined effects of oscillation and current. The study of many oscillatory flow problems arises due to the fact that most marine platform type structures are fixed or at most undergo limited motions, and are subject to the oscillatory velocity component induced by passing waves. In these cases the current is normally of smaller amplitude than the important wave induced velocities. Some common ground is to be found between these problems and the work presented here when the current, or forward speed, and the wave are of near equal strengths.
The present investigation is carried out at various levels of idealisation of the physical problem. The problem differs from the undisturbed (i.e. von Kármán) wake problem by the appearance of essentially two new mechanisms: (a) the fact that the local velocity at the cylinder surface is a combination
of a mean component and a smaller wave induced component varying in time, and thus the strengths of the shed vortices vary with time, resulting in a (weak) periodic spatial variation of vortex strengths away from the body, (b) that the vortices in the far wake are subject to a ‘concertina-like' effect in which the wave-induced velocities cause a periodic dilation and extension of the vortex spacing in a sense parallel to the wave direction. The former mechanism (a) is dependent on the wave amplitude and frequency and is approximately independent of the wavelength of the wave, whilst the wavelength is important in the latter mechanism (b). The waves considered in this work have wavelengths many times that of the body size (as is generally the case of towed bodies in the open sea), and thus are not subject to significant diffraction effects around the body.
It is a well known that the idealisation of a vortex street to an infinite system of point vortices is only neutrally stable—that is to say, an infinitesimal disturbance introduced into the system will grow infinitely slowly (Lamb (1932)), and moreover there is only a single configuration of horizontal to vertical vortex spacing for which this neutrally stable configuration holds; all other spacing ratios are unstable. For an assumed two-dimensional flow and an infinite periodic point vortex model, the imposition of an additional two-dimensional approximation to simulate the effect of the wave motion on the point vortices as described by mechanisms (a) and (b) leads to a degeneration or breaking-up of the wake structure (Graham and Arkell (1992)), characterised by a process of vortex pair dissolution, in which vortex pairs are seen to eject from the central wake.
In reality a surface gravity wave induces orbital velocities which decay exponentially with depth in deep water, but are in phase in the plane normal to the wave propagation direction. Therefore a towed vertical cylinder in waves experiences a spanwise variation in velocity which consists of both horizontal and vertical components and leads to three-dimensional vortex shedding, vortex stretching, and inevitably a much more complicated velocity field.
2
Computational Method
Two flow simulation codes were used in the present work. A two-dimensional viscous vortex-in-cell code was developed using a Finite Volume approach. The method uses a streamfunction-vorticity formulation, in which vorticity is convected on moving particles (vortices) and diffusion is carried out on the mesh (see Graham and Arkell (1992)). A three-dimensional vortex code (FEMVOR) has also been developed in order specifically to investigate some of the three-dimensional effects. FEMVOR, as in the two-dimensional code, employs a particle representation of the vorticity field, in this case using vortons:
(1)
where κα is the strength of the αth vor ton, and δ the Dirac delta function. In the present method the velocity field is calculated on a fixed mesh by projecting the volume-integrated vorticity (vortonicity) carried by the moving vortons onto that mesh. Integration of the field equations is performed over fully unstructured tetrahedral-element meshes using a piecewise linear Galerkin Finite Element method; this allows for compact coding and efficient spatial representation. The mesh generator was the FELISA system (Peraire, Morgan and Peiro (1990)), which is an Advancing Front type and is highly efficient for complex geometries and allows the user to modify mesh densities through application of point, line and triangular source distributions.
Vortonicity is interpolated from the particles onto the mesh nodes, and division of this quantity by the node control volume yields values of vorticity on the mesh. Changes to the vorticity field which arise through diffusion and stretching are re-interpolated back onto the particles at the end of a time step. New particles are created at mesh nodes if the vorticity magnitude there is finite at the end of a time step and no particles originally contributed to that node. New particles therefore materialise at a diffusion front. The method developed here is a hybrid one—similar to the two-dimensional code —in which only the convection is done by tracking particles, all other processes being implemented
on the mesh. Clearly, this reintroduces a certain amount of mesh dependency, but the unstructured tetrahedral-element mesh affords a great deal of flexibility in the distribution of elements. The solution to the field equations on the mesh is obtained using a preconditioned Conjugate Gradient method. The Lagrangian convection step of the current method using particles introduces minimal numerical diffusion, and is appropriate for modelling the complex vortical structures of separated flows. A detailed description of the method appears in Graham and Arkell (1995).
3
Two-dimensional viscous flow computations
A series of numerical experiments are carried out to study the results of adding a progressive wave to the steady incident flow past a circular cylinder. The characteristics of the flow field are presented in the form of instantaneous plots of point vortices; these demonstrate the dynamics of the vortices in the wake and the overall changing structure of the wake. We start by considering the far field free stream velocity to which the cylinder is subjected:
(2)
where Uc is the translational velocity of the cylinder, uw is the particle orbital speed induced by the wave, ωw is the angular frequency of the wave, and kw the wavenumber of the wave. Equation (2) is the velocity field of a progressive wave of wavelength ![]() travelling in the positive x-direction with a celerity
travelling in the positive x-direction with a celerity ![]() The three-dimensional free surface wave problem also has components of velocity in the direction normal to the free surface (i.e. along the cylinder in this case) such that the divergence of this potential velocity field is identically zero. Since the vertical motions are not accounted for in this two-dimensional analysis, mass is not conserved exactly in the two-dimensional potential field. The solution adopted is to split the temporal and spatial components of the phase of the wave so that the potential velocity field applied at the centroids of the computational elements consists of a steady free stream component plus a planar oscillatory component, whilst the velocity applied to the point vortices also includes the spatial component. The potential velocity field around a cylinder of diameter D=2 is therefore given by:
The three-dimensional free surface wave problem also has components of velocity in the direction normal to the free surface (i.e. along the cylinder in this case) such that the divergence of this potential velocity field is identically zero. Since the vertical motions are not accounted for in this two-dimensional analysis, mass is not conserved exactly in the two-dimensional potential field. The solution adopted is to split the temporal and spatial components of the phase of the wave so that the potential velocity field applied at the centroids of the computational elements consists of a steady free stream component plus a planar oscillatory component, whilst the velocity applied to the point vortices also includes the spatial component. The potential velocity field around a cylinder of diameter D=2 is therefore given by:
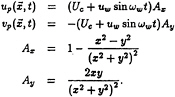
(3)
This velocity field satisfies continuity, i.e. ![]()
![]() The positions of the vortices are updated using the following velocity field:
The positions of the vortices are updated using the following velocity field:
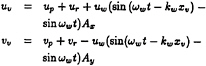
(4)
where subscript p refers to the potential solution, r refers to the rotational or vortical solution, and v refers to the point vortex with integer identifier v.
There are two parameters associated with a wave of height h, which are:
(5)
Once the cylinder is in motion, with speed Uc, a third parameter may be inferred for the relative time scales. A natural choice for this third parameter in this case is the ratio of the frequency of the wave to the natural vortex shedding frequency in the absence of the wave, i.e. ![]() where fn=SUc/D, and S is the Strouhal number. In the cases presented here, the Reynolds number is equal to 150. This is near the upper limit of the two-dimensional vortex shedding regime for steady incident flow, and within the known ‘working range' of the two-dimensional code. The particular case of steady incident flow is presented first so that the effects of waves on the wake structure may be compared with a ‘standard' result. Details of the vortex structures in the near-wake are shown in the point vortex plot for this steady incident flow case (figure 1).
where fn=SUc/D, and S is the Strouhal number. In the cases presented here, the Reynolds number is equal to 150. This is near the upper limit of the two-dimensional vortex shedding regime for steady incident flow, and within the known ‘working range' of the two-dimensional code. The particular case of steady incident flow is presented first so that the effects of waves on the wake structure may be compared with a ‘standard' result. Details of the vortex structures in the near-wake are shown in the point vortex plot for this steady incident flow case (figure 1).
The Strouhal number for the steady incident flow case at this Reynolds number of 150 was found to be 0.182, through measuring the zero-crossings over many periods in the time trace of the transverse velocity field close to the cylinder.

Point vortices. Re=150. No waves.
Figure 1
Figure 2 is a table of the various wave cases studied here. Note that ![]()
|
Case # |
|
|
|
û |
|
1 |
30 |
2.265 |
0.077 |
0.2 |
|
2 |
30 |
2.265 |
0.193 |
0.5 |
|
3 |
30 |
2.000 |
0.087 |
0.2 |
|
4 |
30 |
2.000 |
0.219 |
0.5 |
|
5 |
30 |
1.825 |
0.096 |
0.2 |
|
6 |
30 |
1.825 |
0.240 |
0.5 |
|
7 |
60 |
1.565 |
0.112 |
0.2 |
|
8 |
60 |
1.565 |
0.279 |
0.5 |
|
9 |
60 |
1.295 |
0.135 |
0.2 |
|
10 |
60 |
1.295 |
0.338 |
0.5 |
|
11 |
100 |
1.200 |
0.146 |
0.2 |
|
12 |
100 |
1.200 |
0.364 |
0.5 |
|
13 |
100 |
1.000 |
0.175 |
0.2 |
|
14 |
100 |
1.000 |
0.437 |
0.5 |
|
15 |
200 |
0.690 |
0.253 |
0.2 |
|
16 |
200 |
0.690 |
0.634 |
0.5 |
Summary of wave cases.
Figure 2
The range of ![]() is quite large, and spans the two central values at which lock-in occurs for in-line oscillations
is quite large, and spans the two central values at which lock-in occurs for in-line oscillations ![]() and transverse oscillations
and transverse oscillations ![]() Assuming that, as far as the near wake is concerned, the hydrodynamic effects of in-line oscillations and progressive wave-trains are correlated, the data from Griffin and Ramberg (1976), who conducted experiments on in-line oscillations of a circular cylinder in a steady free stream, indicate that not all the wave cases presented here lie within the lock-in region. Their experiments were carried out at Re=190, which is close to that of the present data. The wave cases are basically divided into two categories of weak (û=0.2) and strong (û=0.5) waves, each being studied over a range of frequencies
Assuming that, as far as the near wake is concerned, the hydrodynamic effects of in-line oscillations and progressive wave-trains are correlated, the data from Griffin and Ramberg (1976), who conducted experiments on in-line oscillations of a circular cylinder in a steady free stream, indicate that not all the wave cases presented here lie within the lock-in region. Their experiments were carried out at Re=190, which is close to that of the present data. The wave cases are basically divided into two categories of weak (û=0.2) and strong (û=0.5) waves, each being studied over a range of frequencies ![]() and amplitudes
and amplitudes ![]() Weak wave case numbers are odd, and strong wave case numbers even. Figures 3 to 10 are plots of point vortices for all weak wave cases presented here, and show the vortex structures of the near-wake. The wakes are shown to a downstream distance of about 30 diameters. The flow is from left to right, and the waves propagate from left to right.
Weak wave case numbers are odd, and strong wave case numbers even. Figures 3 to 10 are plots of point vortices for all weak wave cases presented here, and show the vortex structures of the near-wake. The wakes are shown to a downstream distance of about 30 diameters. The flow is from left to right, and the waves propagate from left to right.

Point vortices. Re=150. Case 1.
Figure 3

Point vortices. Re=150. Case 3.
Figure 4

Point vortices. Re=150. Case 5.
Figure 5

Point vortices. Re=150. Case 7.
Figure 6

Point vortices. Re=150. Case 9.
Figure 7

Point vortices. Re=150. Case 11.
Figure 8

Point vortices. Re=150. Case 13.
Figure 9

Point vortices. Re=150. Case 15.
Figure 10
The characteristics of the wakes in the weak and strong wave cases are quite different. For weak wave cases for which ![]() (cases 3,5,7), the wake is regular and closely resembles that of the steady incident flow case, in which alternate sighed vortices are shed to form a staggered street. This is true even at very large distances downstream. It seems that for waves of this amplitude and within this frequency band, the stability of the resultant street is similar to the steady incident flow case. Case 3 most resembles the steady incident flow case, but as the frequency of the wave decreases, and the amplitude increases, the staggered structure of the wake is lost. At frequencies outside this range, the alternate pattern is disrupted fairly close to the cylinder. In the near-wake, the inter-vortex spacing is no longer regular, and the formation of vortex pairs is apparent (see figure 10). The irregularity of the inter-vortex spacing is generally small; the formation of a definite vortex pair is slow, and takes place several diameters downstream of the cylinder. Often, the vortex pair results from the interaction of three closely spaced vortices; such a vortex triplet may be seen at x/D ≈ 24 in figure 8. In weak wave cases the vortex pairs are not able to travel too far in the transverse sense due to the small differences in vortex strengths and inter-vortex spacings. The result is that the shape of the wake is mildly jagged (figure 11), and not particularly broad far downstream of the cylinder, by which time of course, the vortex strengths have been greatly diminished by diffusion and vorticity cancellation. The far wakes of these cases are sometimes characterised by the presence of large vortex structures, which arise through the coalescence of like-signed vortices. In general, the vortices in these cases are not so compactly arranged, and once the staggered configuration has been interrupted close to the cylinder, the vortices tend to spread out in the longitudinal sense, with the lengthscale of the vortex structures increasing with distance downstream.
(cases 3,5,7), the wake is regular and closely resembles that of the steady incident flow case, in which alternate sighed vortices are shed to form a staggered street. This is true even at very large distances downstream. It seems that for waves of this amplitude and within this frequency band, the stability of the resultant street is similar to the steady incident flow case. Case 3 most resembles the steady incident flow case, but as the frequency of the wave decreases, and the amplitude increases, the staggered structure of the wake is lost. At frequencies outside this range, the alternate pattern is disrupted fairly close to the cylinder. In the near-wake, the inter-vortex spacing is no longer regular, and the formation of vortex pairs is apparent (see figure 10). The irregularity of the inter-vortex spacing is generally small; the formation of a definite vortex pair is slow, and takes place several diameters downstream of the cylinder. Often, the vortex pair results from the interaction of three closely spaced vortices; such a vortex triplet may be seen at x/D ≈ 24 in figure 8. In weak wave cases the vortex pairs are not able to travel too far in the transverse sense due to the small differences in vortex strengths and inter-vortex spacings. The result is that the shape of the wake is mildly jagged (figure 11), and not particularly broad far downstream of the cylinder, by which time of course, the vortex strengths have been greatly diminished by diffusion and vorticity cancellation. The far wakes of these cases are sometimes characterised by the presence of large vortex structures, which arise through the coalescence of like-signed vortices. In general, the vortices in these cases are not so compactly arranged, and once the staggered configuration has been interrupted close to the cylinder, the vortices tend to spread out in the longitudinal sense, with the lengthscale of the vortex structures increasing with distance downstream.
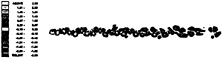
Vorticity contours. Re=150. Case 9.
Figure 11
If the transverse velocity field is sampled close to the cylinder (x/D=2.5, y/D=1.5), it is observed that in cases (3,5,7) the period of the fluctuation in velocity is equal to twice the wave period. The vortex shedding has become synchronised with the wave. This synchronisation phenomenon, in which the wave is of sufficient amplitude and appropriate period to dictate the formation and shedding processes is similar to cases of oscillation of a cylinder in a uniform flow. This has been studied for the
case of cylinders and cables vibrating in-line (e.g. Griffin and Ramberg (1976)) and transversely (e.g. Meneghini (1993)). Time traces of the transverse velocity in the near wake indicate that for cases 3,5 and 7, the vortex shedding is locked on to twice the wave frequency.
From the corresponding point vortex plots of these cases (i.e. figures 3 to 10), it is possible to measure the longitudinal inter-vortex spacing (a). Figure 13 is a plot of the values of the non-dimensional longitudinal inter-vortex spacing (a/D) versus non-dimensional frequency ![]() This plot applies to the synchronised cases only (3,5,7), although the special case of the
This plot applies to the synchronised cases only (3,5,7), although the special case of the ![]() (case 13) is also included (filled circle). The longitudinal inter-vortex spacing in this case is the same as the steady incident flow case.
(case 13) is also included (filled circle). The longitudinal inter-vortex spacing in this case is the same as the steady incident flow case.
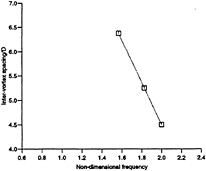
Variation of vortex spacing with frequency.
Figure 13
The three co-linear data points in figure 13 lie on a line of equation:
(6)
Figure 13 shows that for cases with non-dimensional frequency less than about 2.0 the longitudinal inter-vortex spacing is greater than the steady incident flow case, whilst for cases in which the non-dimensional frequency is greater than about 2.0, the longitudinal inter-vortex spacing is smaller.
The strong wave cases ![]()
![]() generally have broader wakes, and demonstrate a rich variety of vortex configurations. Figures 14 to 21 are point vortex plots for these cases. These plots are arranged in an order of descending frequency, increasing amplitude. The flow is from left to right, and the waves are propagating from left to right.
generally have broader wakes, and demonstrate a rich variety of vortex configurations. Figures 14 to 21 are point vortex plots for these cases. These plots are arranged in an order of descending frequency, increasing amplitude. The flow is from left to right, and the waves are propagating from left to right.

Point vortices. Re=150. Case 2.
Figure 14

Point vortices. Re=150. Case 4.
Figure 15

Point vortices. Re=150. Case 6.
Figure 16
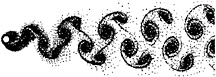
Point vortices. Re=150. Case 8.
Figure 17

Point vortices. Re=150. Case 10.
Figure 18

Point vortices. Re=150. Case 12.
Figure 19

Point vortices. Re=150. Case 14.
Figure 20

Point vortices. Re=150. Case 16.
Figure 21
Case 2 (figure 14) is quite similar to its weaker counterpart (case 1, figure 8). The inter-vortex spacing is not regular, and there is some evidence of vortices ‘bunching' in the near wake. The far wake becomes broad, whilst the longitudinal inter-vortex spacing increases with distance downstream. Figure 22 is a vorticity contour plot of this case.
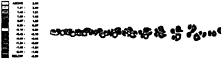
Vorticity contours. Re=150. Case 2.
Figure 22
Case 4 is the special case of ![]() i.e. the wave frequency is exactly twice the natural shedding frequency. The wake structure consists of alternately shed vortices of opposite sign; however, the transverse inter-vortex spacing is large and has a value of 2.75D in the near wake. This compares with 1.5D for the steady incident flow case. The longitudinal inter-vortex spacing has the same value of 4.75D. Figure 23 shows that the wake undergoes a sudden transition at a downstream distance of approximately 70D, after which the vortex structures become larger and the longitudinal inter-vortex spacing increases; meanwhile, the wake undergoes very little broadening, even far from the cylinder.
i.e. the wave frequency is exactly twice the natural shedding frequency. The wake structure consists of alternately shed vortices of opposite sign; however, the transverse inter-vortex spacing is large and has a value of 2.75D in the near wake. This compares with 1.5D for the steady incident flow case. The longitudinal inter-vortex spacing has the same value of 4.75D. Figure 23 shows that the wake undergoes a sudden transition at a downstream distance of approximately 70D, after which the vortex structures become larger and the longitudinal inter-vortex spacing increases; meanwhile, the wake undergoes very little broadening, even far from the cylinder.

Vorticity contours. Re=150. Case 4.
Figure 23
If the wave frequency is lowered, a change in the mode of vortex shedding is seen to occur. Figure 16 is a plot of the point vortices in case 6 ![]() In the near wake it may be seen that a symmetric mode occurs over the region 7.5D≤x≤16D. Further downstream, vortices of like-sign merge, and an anti-symmetric street is realised. At
In the near wake it may be seen that a symmetric mode occurs over the region 7.5D≤x≤16D. Further downstream, vortices of like-sign merge, and an anti-symmetric street is realised. At ![]() (figure 17), the transverse distance between vortices increases so that no merging of vortices occurs, and a double vortex street is established. This configuration persists far downstream, and is seen to exist up to the edge of the computational domain (x=115D). The configuration observed in case 8 is very similar to the flow visualisation data presented by Detemple and Eckelmann (1989), in which the steady flow past a cylinder is acoustically disturbed by inline waves at a non-dimensional frequency of
(figure 17), the transverse distance between vortices increases so that no merging of vortices occurs, and a double vortex street is established. This configuration persists far downstream, and is seen to exist up to the edge of the computational domain (x=115D). The configuration observed in case 8 is very similar to the flow visualisation data presented by Detemple and Eckelmann (1989), in which the steady flow past a cylinder is acoustically disturbed by inline waves at a non-dimensional frequency of ![]() The structures observed in the wake are termed “Sea-horses”.
The structures observed in the wake are termed “Sea-horses”.
At still lower non-dimensional frequencies, the wake structure undergoes further change. Case 10 (figure 18) shows that the wake is mainly comprised of alternately shed vortices, for which the transverse spacing is quite small. One particularly interesting aspect of both this case and the very similar case 12, is that the vortex rows have become interchanged compared with the classical von Kármán vortex street, i.e. vortices with ve circulation form the top row, whilst vortices with +ve circulation form the lower row. This
is characteristic of a typical wake configuration of a body generating thrust. The longitudinal inter-vortex spacing is approximately double that of the von Kármán value. Plots of contours of vorticity for a larger portion of the wake indicate that broadening of these wakes is rapid, and occurs as a result of a vortex pair dissolution process (see figure 24).

Vorticity contours. Re=150. Case 10.
Figure 24
At ![]() (case 14), the near wake consists of pairs of primary vortices which have formed from vortex triplets; in between these three vortices are weaker vortices. This particular case demonstrates the most rapid broadening of the wake (see figure 25), and the differences between this case and the weak wave counterpart (case 13) are marked.
(case 14), the near wake consists of pairs of primary vortices which have formed from vortex triplets; in between these three vortices are weaker vortices. This particular case demonstrates the most rapid broadening of the wake (see figure 25), and the differences between this case and the weak wave counterpart (case 13) are marked.
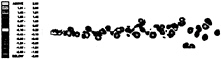
Vorticity contours. Re=150. Case 14.
Figure 25
At wave frequencies below the natural shedding frequency the wake is seen to consist of a regular line of closely formed vortex pairs, which move in a transverse flow sense under their mutually induced velocity field (figure 21). Samples of transverse velocity at x/D=2.5, y/D=1.5 show that the shedding is locked-in, and has a period equal to the wave period. This case indicates that there is a second lock-in region in the ![]() parameter space for
parameter space for ![]() Detemple and Eckelmann (1989) report lock-in for the range
Detemple and Eckelmann (1989) report lock-in for the range ![]() For
For ![]() they report that the vortex shedding experiences lock-in at the driving frequency, and over
they report that the vortex shedding experiences lock-in at the driving frequency, and over ![]() the vortex shedding experiences lock-in at half the driving frequency. In the overlapping range, the mode of lock-in is unpredictable, and sometimes may not occur.
the vortex shedding experiences lock-in at half the driving frequency. In the overlapping range, the mode of lock-in is unpredictable, and sometimes may not occur.
4
Three-dimensional Aspects
The work presented in this paper has so far examined the modifications which take place in the wake as a result of a two-dimensional progressive wave train, which models the presence of a surface gravity wave. However, it has long been recognised (e.g. Williamson (1995)) that even in the case of a two-dimensional incident flow past a nominally two-dimensional body, the rôle of three-dimensional instabilities in the development of the wake is of crucial importance to the structure of the wake. On this basis, the case of a circular cylinder translating into surface gravity waves, for which the incident flow is highly three-dimensional, merits an investigation into the three-dimensional aspects of the wake. Unfortunately, the number of degrees of freedom that exist in the three-dimensional numerical problem is very large, even for the relatively low Reynolds numbers under consideration here. Thus there exist quite severe restrictions on the numerical computations in terms of the length of wake which might be modelled and the spatial accuracy of the solutions.
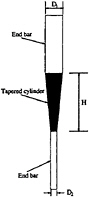
As a prelude to studying surface wave effects on the vortex wake of a circular cylinder, the flow past a mildly tapered cylinder with diameters D1 and D2 at sections H apart is analysed. This flow was initially studied experimentally by Gaster (1969), and has been shown to demonstrate three-dimensional Y-type structures in the wake, which arise through cellular shedding vortex patterns. The taper ratio (Tr) is defined as Tr=H/(D1–D2), and for the case under consideration here has the value of Tr=40. The Reynolds number is 200, based on the midspan diameter, and the aspect ratio is 8. Figure 26 is a plot of the vortons in the flow field after several shedding cycles have taken place. It quite clearly shows the existence of Y-type vortices. In this plot the larger end is at the top. The boundary conditions for the two end
planes are symmetry conditions which support no in-plane components of vorticity; thus, the vortices meet these planes orthogonally.

Vorton plot. Tapered cylinder. Tr=40
Figure 26
Piccirillo and Van Atta (1993) found that the non-dimensionalised cell size became a constant value for a range of taper ratios at Reynolds number greater than about 100. Figure 27 is a reproduction of their figure for the non-dimensional cell size versus the Reynolds number at the centre of the cell. Included on this figure is the data for the case run here; only the larger cell is plotted, which agrees reasonably well with their data. The cylinders used by Piccirillo and Van Atta are of an aspect ratio roughly 5 to 6 times greater than the cylinder tested here, and so the possible number of cells generated is higher. Their data indicate that the cell sizes decrease slowly in the direction of the smaller end. The second cell in the present data (i.e. that nearer the smaller end) has become shortened, because the cylinder length cannot accommodate a full cell. Roughly speaking, a cylinder of aspect ratio of at least 12 at this taper ratio is required for two complete cells.
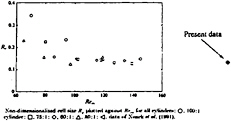
From Piccirillo and Van Atta (1993)
Figure 27
Figure 28 is a velocity vector plot at various spanwise locations for the case computed here. It shows the lack of correlation in the spanwise sense, and indicates that the shedding phase is dictated by the larger end over the majority of the cylinder length.
Velocity vectors at various spanwise locations
Figure 28
An experimental visualisation of this flow is performed for an identical tapered cylinder geometry. The method used is an electrolytic precipitation technique, as detailed in Honji, Taneda and Tatsuno (1980). The experiments
are carried out in the water flume in the hydraulics laboratory of the Department of Aeronautics at Imperial College. The working section is 0.6m wide and 0.65m deep. Non-tapered cylinders are connected at either end of the tapered cylinder. The larger end protrudes through the water surface, whilst at the lower end a 15cm circular end plate is attached. A schematic of the tapered cylinder is shown in figure 29.
Schematic of tapered cylinder
Figure 29
The Reynolds number of the flow is 200 based on the mid-span diameter. A very thin strip of rolled solder the length of the cylinder is attached to the front of the cylinder and is connected to the anode of a low voltage d.c. supply. The cathode is connected to a large steel plate placed many body lengths from the cylinder; when the current is switched on, a whitish precipitate forms at the anode and is drawn into the shear layers, marking the flow patterns. A 5 watt argon ion laser is used to illuminate a thin vertical plane of the wake. Figure 30 is a digitised frame from the video recording of this flow. It shows that the wake is characterised by bi-cellular shedding. The two ends of the cylinder have two different shedding frequencies and a linear variation in diameter implies a linear variation in Strouhal number along each cell. Since the vortex lines formed by the rolled up shear layer must be continuous from the top of the cylinder to the bottom, the disparity in shedding frequency across the cells results in a dislocation or splitting of the vortex.

Precipitate in the wake of a tapered cylinder
Bi-cellular shedding
Figure 30
A three-dimensional numerical simulation of the towed cylinder in waves has also been carried out. The free surface is approximated by the usual linearised wave boundary condition. A transformation is applied to the computational mesh which is exactly equal and opposite to the vertical w-component of the basic potential velocity.
An unstructured mesh with 400,000 tetrahedra is used for the computation. Figure 31 is an x–y plane through the mesh, and figure 32 shows both an x–y and a y–z plane. The mesh is first generated over the interval 0≤z≤1.0, and then stretched in the z-direction, so that the aspect ratio of the cylinder is 16.

x–y plane in the mesh
Figure 31
x–y and y–z planes in the mesh
Figure 32
A case is run for ![]()
![]() Figure 33 shows the vortons at a non-dimensional time of t*=68.4. The top plot is a plan view on to the free surface; the middle plot is a three-dimensional perspective of the flow field, and the bottom plot is a plan view of the flow at z=–H. The middle plot shows only three slices of the vorton field, otherwise the image would be too complicated to interpret. At this point in the computation there are just over 2×106 vortons in the field. Here, the free surface is shown as a grid. The cylinder is travelling from left to right, the waves from right to left, and the viewer is looking down on the cylinder; a small length of cylinder is drawn protruding through the free surface. The length of the cylinder is approximately equal to λw/4, meaning that the u-component of the wave velocity field spans the approximate range: û: 0.2 → 0.5 between the bottom (z=–H), and the free surface (z=0). Figure 33 shows that near to the free surface the vortex shedding is almost symmetric. In the bottom plane the near-wake resembles the von K ármán vortex street. The middle plane near-wake flow is quite similar to the two-dimensional result of Case 6, and the correlation between this plane and the free surface is high over this region. It is difficult to visualise what is happening to the vortices in the wake in a three-dimensional sense; the flow behind the tapered cylinder has been shown to be structurally quite simple, but what form of vortex connection is taking place here is hard to say. More insight may be gained by forming iso-vorticity surfaces from the data, and examining the way in which these ‘structures' behave in the wake.
Figure 33 shows the vortons at a non-dimensional time of t*=68.4. The top plot is a plan view on to the free surface; the middle plot is a three-dimensional perspective of the flow field, and the bottom plot is a plan view of the flow at z=–H. The middle plot shows only three slices of the vorton field, otherwise the image would be too complicated to interpret. At this point in the computation there are just over 2×106 vortons in the field. Here, the free surface is shown as a grid. The cylinder is travelling from left to right, the waves from right to left, and the viewer is looking down on the cylinder; a small length of cylinder is drawn protruding through the free surface. The length of the cylinder is approximately equal to λw/4, meaning that the u-component of the wave velocity field spans the approximate range: û: 0.2 → 0.5 between the bottom (z=–H), and the free surface (z=0). Figure 33 shows that near to the free surface the vortex shedding is almost symmetric. In the bottom plane the near-wake resembles the von K ármán vortex street. The middle plane near-wake flow is quite similar to the two-dimensional result of Case 6, and the correlation between this plane and the free surface is high over this region. It is difficult to visualise what is happening to the vortices in the wake in a three-dimensional sense; the flow behind the tapered cylinder has been shown to be structurally quite simple, but what form of vortex connection is taking place here is hard to say. More insight may be gained by forming iso-vorticity surfaces from the data, and examining the way in which these ‘structures' behave in the wake.
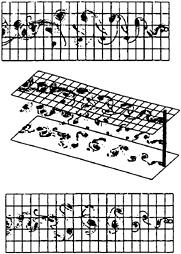
Vorton plot. ![]()
Figure 33
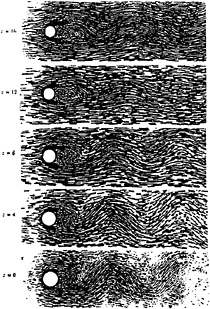
A series of flow visualisation experiments are carried out in the 20m wave flume in the Department of Aeronautics, Imperial College to examine the free surface vortices of the wake of a vertical cylinder translating steadily into waves. The working section of this flume is 0.6m wide, 3 metres long, and typically has a depth of about 0.8m. The twin-paddles which create the waves may be driven over the frequency range of 0.5 → 2.5Hz, giving a range of wavelengths of between 6.25m and 0.25m. A signal generator is used with a sinusoidal output signal.
The cylinder penetrates the free surface, and has minimum clearance at the bottom of the flume. The Reynolds number of the experiments is 600. Visualisation is achieved by bleeding a solution of potassium permanganate on to the front part of the cylinder. This is done through a hypodermic needle to help maintain an even, minimal flow rate whilst avoiding the formation of droplets of dye. Two 1000 Watt tungsten lights either side of the working section provide illumination. Fairly high speed (400 ASA) black and white film is used in a camera mounted above the water surface and fixed relative to the flume. Figure 34 demonstrates the formation of the classical von Kármán vortex street which re-
mains stable up to about 30D downstream; thereafter structure in the flow patterns becomes much less distinct and there is a small but fairly abrupt change in the wake width. There is a slight bias in concentration of dye, which makes the vortices on the lower row appear a little darker.
Free surface flow visualisation
Cylinder in steady translation
Figure 34
Figure 35 demonstrates the effects of adding a wave of ![]() The vortex patterns that emerge in the wake are similar to the “Sea-horses” of Detemple and Eckelmann (1989). The parameters of this case lie in between those of case 8 and case 10 of the two-dimensional viscous analysis data (figures 17 and 18 respectively). The structure of the near wake in the experiment most closely resembles that of case 8, although the inter-vortex spacing is not quite as small as that of the numerical simulation. At a streamwise distance of about 20D from the cylinder, this double street pattern is replaced by a different configuration which consists of a single vortex in the lower row and a complex arrangement in the upper row. whilst the flow field in the upper row has become quite complex. The vorticity contour plot for case 10 (figure 24) shows a similar behaviour at around a downstream distance of 35 diameters.
The vortex patterns that emerge in the wake are similar to the “Sea-horses” of Detemple and Eckelmann (1989). The parameters of this case lie in between those of case 8 and case 10 of the two-dimensional viscous analysis data (figures 17 and 18 respectively). The structure of the near wake in the experiment most closely resembles that of case 8, although the inter-vortex spacing is not quite as small as that of the numerical simulation. At a streamwise distance of about 20D from the cylinder, this double street pattern is replaced by a different configuration which consists of a single vortex in the lower row and a complex arrangement in the upper row. whilst the flow field in the upper row has become quite complex. The vorticity contour plot for case 10 (figure 24) shows a similar behaviour at around a downstream distance of 35 diameters.
For longer wavelength, lower frequency waves, a different flow pattern emerges. Figure 36 is a photograph for the case ![]() The wake is characterised by the presence of large vortex pairs in the upper half plane, and a single vortex in the lower half plane. The vortex pairs apparently convect quite rapidly in a transverse sense, so that at a streamwise distance of about 30D from the cylinder, the wake is very broad; dye has spread over approximately twice the transverse distance when compared with the no wave result. The parameters in this case are very close to case 14 of the two-dimensional viscous analysis, and there are similarities in the data. Figure 37 is a plot of the numerical data for approximately the same length of wake as in the experimental photograph.
The wake is characterised by the presence of large vortex pairs in the upper half plane, and a single vortex in the lower half plane. The vortex pairs apparently convect quite rapidly in a transverse sense, so that at a streamwise distance of about 30D from the cylinder, the wake is very broad; dye has spread over approximately twice the transverse distance when compared with the no wave result. The parameters in this case are very close to case 14 of the two-dimensional viscous analysis, and there are similarities in the data. Figure 37 is a plot of the numerical data for approximately the same length of wake as in the experimental photograph.
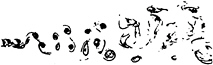
Free surface flow visualisation
![]()
Figure 35
Figure 37 is fairly close to being a mirror image of the experimental data; the vortex pairs in this case are in the lower half plane, and the single vortex is almost directly above the corresponding pair. Notice also that in between the single vortex and the next downstream vortex pair there exists a smaller vortex in the connecting free shear layer. This is just observable in the experimental data of figure 36 between the two vortex pairs closest to the cylinder. Further downstream there is no evidence of a formed vortex at this location (also true of the numerical data), which may be related to the local strain field exerted by the rapid transverse motion of the next downstream vortex pair. The formation of the first vortex pair in the numerical data occurs further from the cylinder than in the experimental data; indeed, the entire wake pattern is more stretched in the longitudinal sense, and the vortex pairs themselves travel a smaller distance in the transverse sense. This may be a result of the difference in Reynolds number between the two sets of data.

Free surface flow visualisation
![]()
Figure 36

Point vortices. Re=150. Case 14
Figure 37
5
Conclusions
Results have been presented of both 2-D and 3-D computations of the vortex wake behind a cylinder towed through waves. The computations are at a Reynolds number of 150. A survey of the changing wake patterns as a function of the wave parameters is presented. These data are in good qualitative agreement with both data in the literature on vertical cylinders in steady flow undergoing in-line oscillations, and surface flow visualisation data conducted in the Department of Aeronautics wave flume. A 3-D computation proved computationally expensive, but demonstrated reasonable agreement with the 2-D computations, and provides useful experience for future research in this direction. A 3-D computation of flow past a linearly tapered cylinder in a steady current is also presented. The data show the spanwise cell formation observed in flow visualisation experiments carried out by the authors on an identical geometry.
6
Acknowledgements
This work was supported by the Office of Naval Research under contract No. N00014–90-J-4122.
7
References
E.Detemple-Laake and H.Eckelmann. Phenomenology of Kármán vortex streets in oscillatory flow. Exp. Fluids, 7:217–27, 1989.
M.Gaster. Vortex shedding from slender cones at low Reynolds numbers. J. Fluid Mech., 38:565–76, 1969.
J.M.R.Graham and R.H.Arkell. End of contract reports to ONR. Contract No. N00014– 90-J-4122. 1992 and 1995.
O.M.Griffin and S.E.Ramberg. Vortex shedding from a cylinder vibrating in line with an incident uniform flow. J. Fluid Mech., 75:257– 71, 1976.
H.Honji, S.Taneda and M.Tatsuno. Some practical details of the electrolytic precipitation method of flow visualization. Technical Report 89, Research Institute for Applied Mechanics, Kyushu University, 1980.
H.Lamb. Hydrodynamics. Cambridge Univ. Press, 1932.
J.Meneghini. Numerical Simulation of bluff body flow control using a discrete vortex method. PhD Thesis, Imperial College, London, 1993.
J.Peiro, J.Peraire and K.Morgan. FELISA System, Reference Manua.l 1994.
P.S.Piccirillo and C.W.Van Atta. An experimental study of vortex shedding behind a linearly tapered cylinder at low Reynolds number. J. Fluid Mech., 246:163–95, 1993.
C.H.K.Williamson. Three-dimensional vortex dynamics in the wake of a cylinder. In Fluid vortices, ed. S.I.Green. Dordrecht: Klumer Academic, 1995.













