Bluff Body Hydrodynamics
P.Bearman (Imperial College of Science, Technology and Medicine, United Kingdom)
SUMMARY
This paper presents some issues related to the fluid dynamics of bluff bodies in steady currents and in oscilatory flows. The importance of vortex shedding and its three-dimensional structure, even from two-dimensional geometries, is discussed. Vortex shedding patterns from a circular cylinder in oscillatory flow are reviewed. The potential for applying CFD in bluff body hydrodynamics is discussed and results are presented for the forces on a fixed cylinder and for the response of a flexible cylinder.
INTRODUCTION
Bluff body hydrodynamics is a general term that may be used in the naval field to describe the study of hydrodynamics of floating and fixed structures that generate significant regions of separated flow. Clearly bluff body aerodynamics and bluff body hydrodynamics are closely related but in the naval context the presence of an air/water interface and surface waves introduce additional phenomena that are absent in aerodynamic flows. A common feature of bluff body flows is that they are complex and often difficult to predict. In practical naval bluff body flows, Reynolds numbers are usually high and in a range where disturbances are massively amplified through instability mechanisms. This leads to both turbulence, i.e. multi-scale, random, three-dimensional motion, and the generation and shedding of large coherent vortex structures. Both types of motion may have a profound effect on the fluid loading of marine structures.
A bluff body can be defined as a body that, as a result of its shape, has separated flow over a substantial part of its surface. An important feature of a bluff body flow is that there is a very strong interaction between the viscous and inviscid regions. If we consider that at the moment of starting the flow is attached, then the adverse pressure gradients that this flow imposes on the boundary layer will be too great to sustain the attachment. Separation may occur either from sharp edges or from a continuous surface. Prediction of separation position from a continuous surface is particularly difficult because it depends on both the characteristics of the upstream boundary layer and on the structure of the near wake region. Also the separation position may move in response to pressure gradients imposed by unsteady flow features in the wake. Usually bluff bodies induce flow separation at positions where the velocity at the edge of the boundary layer is higher than the free stream velocity. This leads to a high rate of shedding of circulation which in turn leads to a high drag. Also due to the generation and shedding of coherent vortices, large unsteady forces may develop, particularly in a direction transverse to the flow direction.
Ships are usually designed to avoid large areas of flow separation in forward motion, although in practice there may be some separation at the stern. However, when moored or when manoeuvring at low speeds the relative flow velocity due to currents, waves and perhaps large roll motion may induce substantial separations. For example, to help minimise the response of moored vessels used by the oil industry for floating production and storage offshore (FPSOs), it is important to have reliable systems in place to control the heading. However, the traditional types of floating and fixed offshore structure used for oil recovery can expect waves and
currents from any direction and they are designed using bluff cross sections, such as the circle and the square. Hence the offshore structure designer needs to have some knowledge of bluff body hydrodynamics.
Within the field of naval architecture ideal flow theory has been used very successfully to estimate wave-induced motions and loads on large floating structures. However, it cannot be used to model realistically phenomena resulting from the viscous nature of water such as boundary layers, flow separation and vortex generation and shedding. Bluff body hydrodynamics is concerned with real fluids and with understanding the effects of flow separation. Traditionally bluff body flows have been studied experimentally with relatively simple models developed to provide ways of correlating data. As computer power has increased more and more CFD studies of bluff body flows are becoming available, based on numerical simulations of the unsteady Navier Stokes equations. In some applications, such as predicting the slow drift response of moored structures, predictions from ideal flow theory are being combined with results from bluff body research. The drag arising from viscous effects is treated as a form of hydrodynamic damping which is considered as independent of the primary loading which is developed by waves. This is an attractive approach but there is a need to validate how successfully flows can be superposed in this way.
Circular cross-section members are a common form used in offshore structures and hence it is fortunate that the circular cylinder is also the most studied bluff body shape. It has geometric simplicity enabling models to be easily manufactured for basic experimental research. Its simple form also makes it attractive as a representative bluff body for CFD investigations. Much of this paper will be concerned with the circular cylinder but such a great deal of research has been carried out using this shape that it is impossible to provide a comprehensive review within the confines of a single paper. Basic questions that will be addressed include: does a bluff body with a two-dimensional geometry placed in a uniform stream generate a two-dimensional flow, what new phenomena appear when a bluff body is placed in waves and how successfully can CFD be used to predict loading and response of bluff bodies?
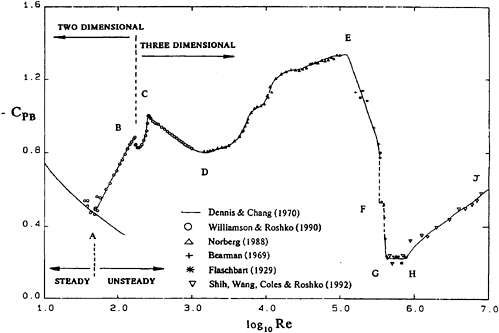
Figure 1 Base Pressure Coefficient versus Reynolds Number for a Circular Cylinder (Roshko (1))
BLUFF BODIES IN A CURRENT
The sensitivity of circular cylinder flow to varying the Reynolds number, Re, where Re=UD/v and U is current velocity, D cylinder diameter and v kinematic viscosity is well illustrated in figure 1 from Roshko(1). Here the pressure in the separated region, or the base pressure, is plotted as a pressure coefficient, Cpb, for a wide range of Reynolds numbers. The variations in Cpb with increasing Re are linked to the growth of disturbances occuring in different regions of the flow; first in the near wake, then in the free shear layers and finally in the boundary layer. Disturbances introduced externally, say by turbulence in the approaching flow or by surface roughness, may modify the shape of figure 1. In an ocean environment roughness, in the form of various species of marine life, may attach itself to a cylinder and substantially change the fluid loading. This often leads to increased drag and stronger vortex shedding. In this paper it will not be possible to discuss these aspects in detail and bluff body surfaces will be assumed smooth and approaching currents will have minimal levels of turbulence.
The vortex shedding frequency, n, is normally presented in non-dimensional form as a Strouhal number, S, where S=nD/U. The value of the Stouhal number varies from one bluff body to another and, as in the case of a circular cylinder, it may change with changing Re. In general, the bluffer the body then the lower the value of S. A number of researchers have proposed that if Strouhal number is based on appropriate wake parameters then it should take a universal value, regardless of body shape. The best known universal Strouhal number, S*, is that due to Roshko(2). He proposed that rather than use the free stream velocity, the velocity just outside the shear layer at separation, Ub, should appear in S*. This velocity is related to the base pressure by the expression Ub=U(1–Cpb)1/2. Also he argued that the length scale in the universal Strouhal number should be related to the distance between the free shear layers as they roll up to form vortices. He obtained this length theoretically using a notched hodograph method (Roshko(3)). Later other workers, most notably Griffin (4), carried out experiments to measure this distance for a large range of bluff body shapes. A compilation of results for a variety of bluff bodies, gathered together by Griffin, is plotted in figure 2 where it can be seen that a roughly constant value of S* is obtained. The scatter in this data arises most likely from two causes:
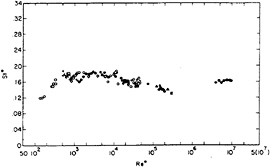
Figure 2 Universal Strouhal No versus Reynolds No for a variety of bluff body shapes (Griffin (4))
experimental error and physical processes of secondary importance which have only a weak effect on the shedding frequency.
Above a Reynolds number of about 150 to 200, vortex shedding from nominally two-dimensional bluff bodies exhibits certain three-dimensional characteristics, irrespective of how carefully the experiment is carried out. A simple way of quantifying this three-dimensionality is to measure the spanwise correlation length of some property related to vortex shedding, such as fluctuating pressure on the body surface, fluctuating velocity in the wake or local fluctuating lift. For many shapes of bluff body the correlation length at moderate and high Reynolds numbers is equal to just a few body diameters. This length cannot be predicted theoretically and the mechanisms responsible for limiting spanwise correlation are not fully understood. A number of authors have presented measurements of the spanwise correlation length for flows with regular vortex shedding. For example, Szepessy (5) has investigated the correlation of vortex shedding from a circular cylinder at a high subcritical Reynolds number. While on average vortices are shed parallel to the cylinder axis, he shows that instantaneously there are substantial variations in the phase of vortex shedding over relatively short spanwise distances.
Gerrard (6) was one of the first to study in detail the three-dimensionality of cylinder wakes. He identified three important ways in which vortex shedding may deviate from a two-dimensional form: oblique shedding in which vortices are shed at a small angle to the cylinder axis, the splitting or dislocation of vortices of similar sign and the
looping of vortices across to the other side of the wake. Vortex looping is a particularly strong form of three-dimensionality in which a vortex joins with one or more vortices of opposite sign on the other side of the wake. Examples of where it might occur are at a free end or where a bluff body meets a wall. Experiments by Williamson (7), Eisenlohr and Eckelmann (8) and Hammache and Gharib (9) on a circular cylinder at Reynolds numbers up to about 150, have all shown that two-dimensional vortex shedding may only be obtained if the cylinder end conditions are very carefully controlled. At higher Reynolds numbers it is still possible to influence the flow by adjusting the end conditions but it is no longer possible to preserve the instantaneous flow in a two dimensional state. A vortex dislocation, or split, has been shown by Eisenlohr and Eckelmann (8) to occur when there is a spanwise variation in the frequency of vortex shedding and it is a means by which vortices of similar sign can connect with each other at a boundary between cells with different shedding frequencies.
The types of three-dimensional vortex motion most often found in the wakes of nominally two-dimensional bluff bodies are oblique shedding and vortex dislocation. Bearman and Tombazis (10) visualised the flow in the wake of a two-dimensional blunt-trailing-edge model fitted with end plates and mounted in a water tunnel. The Reynolds number of their experiment, based on trailing-edge thickness, was 2,500 and they found that departures from two-dimensional vortex shedding appear to occur at random points along the span and at irregular time intervals. Both oblique shedding and vortex dislocations were observed. At this higher Reynolds number there is three-dimensional motion related to spanwise instabilities of the Karman vortices (Triantafyllou (11)), smaller scale three-dimensionality due to shear layer instability (Wei and Smith (12)) and three-dimensional motion associated with turbulence generated in the flow past the bluff body. To what extent these motions interact is unknown.
Since the primary instability mode in the wake of a two-dimensional bluff body is itself two-dimensional, as discussed by Monkewitz and Nguyen (13), it is reasonable to suppose that two-dimensional numerical simulation schemes should be able to successfully predict bluff body flows. However, Szepessy and Bearman (14) measured the fluctuating lift on a thin section of a large aspect ratio circular cylinder and found that two-dimensional simulation schemes generally overestimate the root mean square value of fluctuating lift, in some cases by substantial amounts. This observation has been substantiated by Graham (15) who gathered together numerical predictions for circular cylinder flow and compared them with experimental results. He found that above a Reynolds number of 150 the mean and fluctuating forces were generally over predicted, with the largest differences occurring in the fluctuating lift. It should also be noted that measured time histories of fluctuating lift show a pronounced amplitude modulation whereas simulated time histories mostly display a constant amplitude, once the flow has settled. While some of the differences between measurement and prediction may be due to problems in modelling turbulence it seems likely that the three-dimensional features of vortex shedding should also be modelled. It is interesting to note that several researchers have developed three-dimensional simulation programs to predict nominally two-dimensional bluff body flow. Generally the results from this approach show a closer agreement with experiment.
Key three-dimensional features of the wake of a nominally two-dimensional body appear apparently randomly in time and space. Using a blunt-trailing-edge model, Bearman and Tombazis (10) decided to try to control locations along the span by applying a mild geometric disturbance in the form of a wavy trailing edge. It is not immediately apparent that applying a spanwise wave to the trailing edge of a constant thickness blunt-trailing-edge model will affect the vortex shedding frequency selection process. Two interesting possibilities present themselves: if the vortex formation length is constant along the span then the vortices themselves will be wavy or, if the vortices are two-dimensional, then the base pressure is likely to vary along the span since the vortex formation length varies.
It is well known, for example Bearman (16), that the phase of vortex shedding along the span of a bluff body can be synchronised by oscillating the body or the flow at the shedding frequency. Such a situation arises when a flexible bluff body is excited into oscillation by vortex shedding. A certain threshold amplitude has to be exceeded before extensive regions of correlated vortex shedding are achieved. During these oscillations, which occur over a range of flow speed, the vortex shedding frequency becomes locked to the body oscillation frequency. Under these
circumstances the flow is highly two-dimensional and it is likely that a two-dimensional, direct numerical simulation code will provide accurate predictions.
INFLUENCE OF A THREE-DIMENSIONAL DISTURBANCE
In order to study three dimensional aspects of bluff body wakes, Bearman and Tombazis (10) deliberately introduced three-dimensionally by modifying the base of a bluff body. Wind tunnel and water flume experiments were carried out on a number of bluff body models, each with a nose in the shape of a half ellipse and with a blunt trailing edge
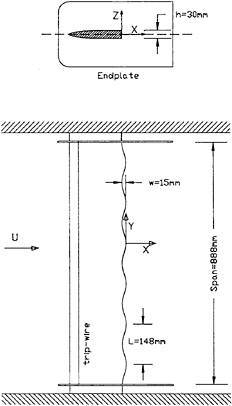
Figure 3 Model with a Sinusoidal Trailing Edge
which was either straight or in the form of a sinusoidal wave. In the wind tunnel experiments the mean chord of the models along their spans was 190mm and the semi-major axis of the nose section was 120mm and the semi-minor axis was 15mm. The remainder of each model was parallel sided giving a base height of 30mm. Eight models were constructed in order to be able to study the effect on the flow of both base wavelength, L, and base peak-to-peak wave height, w. A diagram of a typical model is shown in figure 3. The Reynolds number range, using model base height as the reference length, was from 20,000 to 60,000. Flow visualisation was performed at a Reynolds number of 2,500 in a water flume. As an initial comparison between the various models, the spanwise distribution of mean base pressure was measured. For the straight trailing-edge model a constant value of Cpb was found in a spanwise region of 10h around the mid-span. The value obtained of –0.585 is in good agreement with previous measurements of Bearman (17).
Tanner (18), working with models having a similar cross-sectional shape to the ones studied here, found that by “breaking” the separation line along the span he could achieve significant drag reduction. In accordance with his results, the wavy models have higher (less negative) values of Cpb. The distributions of base pressure coefficient along a half wavelength of the various wavy models (all with a wave height w of 15mm) are shown in figure 4. Measurements on all the wavy models showed distributions of base pressure values that repeated themselves over the spanwise waves between the end plates. A notable feature in figure 4 is that the steeper the wave, where steepness=w/L, the larger the drag reduction. Compared to the straight-edge model, the drag reduction for the models with w/L=0.09,0.10,0.11,0.13 and 0.14 is about 10%,16%,24%,25% and 34% respectively.
A further important feature of figure 4 is the significant difference between the measured values of Cpb at a peak and a valley. All wavy models show a similar trend, with a peak exhibiting less negative values of Cpb than a valley. For the model with L=148mm and w/L=0.1, the value at the valley is about –0.48, with Cpb smoothly increasing to a maximum of –0.44 at the peak. It should be noted that from y/L=0.2 to y/L=0.5 (a valley) the base pressure remains quite constant, the main variations being observed for y/L<0.2, i.e. close to the peak.
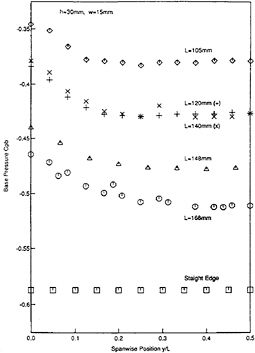
Figure 4 Variation of Base Pressure Coefficient for models with different wavelengths, L; y/L=0 corresponds to a peak in the base.
Power spectra of the velocity records obtained from hot-wire probes were calculated in order to determine the characteristic frequencies of the wakes of the various models. For the straight-edge model the Strouhal number, obtained using the frequency for the dominant peak in a power spectrum, was 0.24 and this is in agreement with the value obtained by Bearman (17).
Figure 5 shows velocity spectra for the wavy model with w/L=0.1, measured at different spanwise distances, y, from the peak in a wave. The main characteristic is the presence of two shedding frequencies with one at a Strouhal number of S=0.24, referred to later as f1, and the other at S=0.29, referred to as f2. At a peak in the base the lower of the two frequencies is the stronger, but as we move towards a valley it weakens (becoming almost undetectable at y/L=0.333) and the high frequency component becomes increasingly strong. The presence of the two frequencies suggests that, at
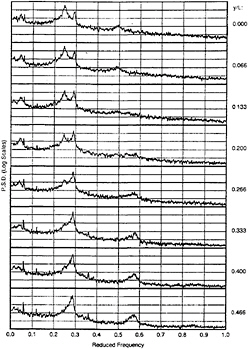
Figure 5 Velocity spectra for a model with w/L= 0.1, at different spanwise positions
least at some times, we have two cells within this spanwise region, corresponding to a half-wavelength of the trailing edge, shedding at different frequencies. Further, it follows that it is highly likely that there is some form of vortex splitting occurring at the boundary between the cells. The velocity spectra for all wavy models follow a similar pattern. Figure 6 shows spectra measured at the peaks of the various wavy models together with the spectrum for the straight trailing-edge model. As the wave steepness, w/L, increases so the higher of the two shedding frequencies become more and more distinct.
The existence of a dual frequency characteristic has been demonstrated by measuring power spectra of fluctuating velocity but what does this means from a physical point of view? We cannot be sure that both of the main peaks in a power spectrum of velocity necessarily reflect the frequency of vortex shedding (at some time instants, at least) at that spanwise position. Does the dual frequency indicate a simultaneous presence of two frequencies,
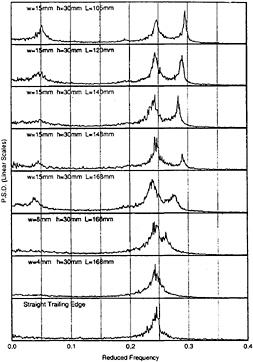
Figure 6 Velocity spectra measured at the peaks of models with various wave steepnesses, w/L
e.g. a signal like C1*sin(2πf1t)+C2*sin(2πf2t), or does it represent an interval of C1*sin(2πf1t), followed by an interval at C2*sin(2πf2t)? In the main it appears that at a particular spanwise position the vortices shed for a while at one frequency and then switch to the other frequency.
Flow visualisation performed in the water flume confirmed the cellular nature of the wake of the sinusoidal trailing-edge model. Figure 7 shows a sequence which indicates the low-frequency periodicity of vortex splitting. The images were extracted from a video tape, with the shots being roughly one shedding cycle apart. From (a) there is little to indicate the complicated three-dimensional nature of the flow. One shedding cycle later, at (b), the cell at the peak has delayed its vortex shedding by a small amount. The vortices from the two neighbouring valleys bow backwards to accommodate this delay. At (c), another cycle later, a further delay at the peak seems to have brought the two cells out of phase. The vortices from the valleys
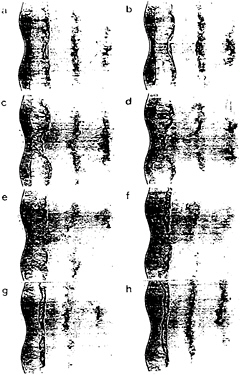
Figure 7 Visualisation in the wake of a model with w/L=0.1, showing successive shedding cycles in the symmetric mode
have bent further back. It appears that when this bowing angle becomes too large then vortex splitting occurs and the vortex from the peak links up with two vortices from each adjacent valley. Eisenlohr and Eckelmann (8) also identified the large oblique bowing angle as one of the characteristics of vortex splitting. Image (d) follows a similar pattern with vortex splitting once again being very pronounced, while from (e) to (h) the phase difference between the two cells reduces and the vortex filaments then become straight again.
An interesting feature of this flow is the persistent way each cell stays at its selected frequency, acting like an oscillator operating at its own characteristic frequency. Even in figures 7 (a) and (b), where the vortices appear to be fairly straight and undisturbed, the cell at the peak is shedding vortices at a slower rate than that at the
adjacent valleys. So that even though the flow may at certain instants seem two-dimensional, the underlying physical mechanisms are always three-dimensional.
In the sequence of pictures in figure 7 the flow is symmetric with respect to the peak. Flow visualisation revealed a total of four modes, here termed symmetric, antisymmetric (two types) and oblique. The oblique mode can be seen in (a)–(d) of figure 8. From these pictures one can see that there is no preferred positive or negative oblique shedding angle, i.e. the oblique mode is not due to an imperfection in the alignment of the model.
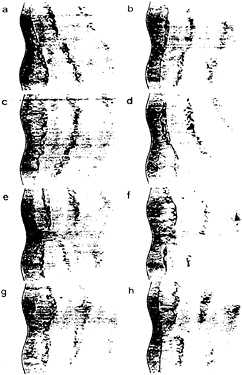
Figure 8 Visualisation in the wake of a model with w/L=0.1: (a) to (d) oblique vortex shedding mode and (e) to (h) antisymmetric vortex shedding mode
In the antisymmetric mode, shown in figure 8 (e) to (h), the vortex shedding in the valleys either side of the peak are in anti-phase. It is unclear in this mode exactly what is happening in the region of the peak. One possibility is that there are two cells, each
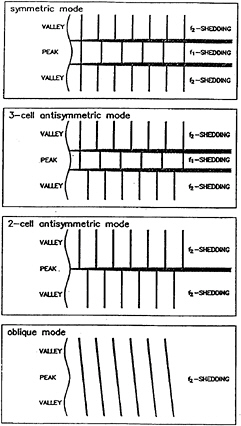
Figure 9 Schematic representation of the various shedding modes: shaded areas represent positions where dislocations occur
associated with a valley and shedding at f2, that extend up to the peak and link up in that region. Another possibility is that there are three cells with shedding frequencies f2 at one valley, f1 at the peak and f2 again at the other valley. The dislocations would then follow a pattern similar to that for the symmetric mode described earlier. It was found that for transition to occur between the symmetric and the oblique modes, both kinds (two-cell and three-cell) of antisymmetric mode must exist.
The flow alternates at seemingly irregular intervals from one mode to another. The transition between the modes does not, as a rule, occur
instantaneously, but is gradual. Thus, in order to understand the flow we have to identify possible intermediate states that may accompany the transition from one mode to another. It is unlikely, for example, that the flow will change directly from a symmetric to an oblique mode because so many features of the wake would have to change instantaneously. Figure 9 provides paths, derived from detailed study of flow visualisation, for the transitions between modes. The modes are ordered in such a way that each one is above or below the other modes which it most closely resembles. It is suggested that when a mode changes it can only “jump” between two consecutive boxes of figure 9, either upwards or downwards.
It was mentioned earlier that the flow would switch between modes at seemingly random intervals. Although a number of mode-transition procedures were proposed above, the actual mechanism of transition is unclear. Obviously a number of questions regarding mode-transition arise. We do not know if the four proposed modes are genuinely “self-contained” modes. They could each conceal a low level instability that gradually forces a change of mode. On the other hand, each of the observed modes could be a stable mode, in the sense that, in the absence of external de-stabilising factors, it could continue ad infinitum. In that case the transitions could be triggered by some irregularities in the flow. However, one thing is clear: all modes would occur, irrespective of initial conditions and after sufficient time had been allowed for the flow to settle.
The general conclusion reached from studies such as the one outlined above is that at high Reynolds numbers three-dimensionally is a very important feature of bluff body wakes, even for wakes generated from nominally two-dimensional geometries. From direct numerical simulation studies at relatively low Reynolds numbers it appears that three-dimensionality has a particularly strong influence on the level of fluctuating transverse force at a local section. Three-dimensional flow mechanisms also control another important aspect of bluff body wakes, the spanwise correlation length of vortex shedding and presently there is no reliable method, apart from experiment, to predict this quantity. It would appear likely that vortex dislocations are present across a wide range of Reynolds numbers. Further research is needed into the three-dimensionality of bluff body wakes particularly for the prediction of loads and responses of cables and riser pipes in uniform and sheared currents.
BLUFF BODIES IN OSCILLATORY FLOW
The ocean flow environment is extremely complex and naval structures are exposed to random wave fields, with directional spreading and possibly a superimposed current. This complexity poses a severe problem for an engineer wishing to calculate the fluid loading on a bluff marine structure. Small scale model tests might be carried out in a wave basin but the results would need careful interpretation because of the sensitivity of viscous flows to scale effects. CFD offers the possibility of an attractive solution but substantial improvements in computational resources are required before this can become a reality. However, researchers are beginning to make the first steps towards numerically simulating the flow about a bluff body in waves and this is likely to be an important growth area.
Much has been achieved by conducting experiments on elementary bluff body shapes in waves and planar oscillatory flow to improve physical understanding and to test empirical models for predicting fluid loading. The object has been to try to uncover the main underlying flow processes and this is often best achieved by carefully restricting the range of variables examined. For example, a wave field may be idealised as a regular train of unidirectional waves or, carrying the idealisation a stage further, the ambient flow may be replaced by a planar, harmonic, oscillatory flow. The latter simplification is the equivalent of using a strip theory approach to predict the loading on a vertical, surface-piercing, circular cylinder in waves. While it does not model the orbiting flow which is characteristic of waves it does reproduce what appears to be the most important feature of a bluff body in waves, i.e. the re encounter with the wake generated in a previous half cycle. The return of a wake containing coherent vortices has a significant influence on future flow development and subsequent vortex shedding. In a random wave field the influence of wake re encounter appears to make the prediction of loading even more complex as it may depend as much on the present wave as on say the influence of previous waves which will have different characteristics.
In a planar, harmonic, oscillatory flow with kinematic viscosity υ and velocity U=Ûsin (2πt/T), where Û is the peak velocity and T is time period, the loading on a cylindrical section of diameter D depends on the following non-dimensional parameters: ÛT/D, ÛD/υ and t/T. ÛT/D is known as the Keulegan Carpenter number, KC, and is often rewritten as 2πA/D, where A is the amplitude of the oscillatory motion. Many authors prefer to replace the Reynolds number, ÛD/υ, by an alternative viscous parameter, D2/υT, which is known as either the Stokes number or the β parameter. KC can be interpreted as being related to the ratio of the distance particles convect during a flow cycle to the cylinder diameter and β can be explained as being related to the ratio of the time it takes for viscosity to diffuse particles a distance equal to the cylinder diameter to the flow time period. For a vertical cylinder in waves KC is a maximum at the surface and decreases with depth but β remains constant over the depth of the cylinder. In a laboratory experiment it is relatively easy to match full scale KC values but β may be up to two or even three orders of magnitude too small. Reynolds number is the product of β and KC and at full scale its peak value is often in a range that in steady current flow would be described as post-critical. Most laboratory experiments have Reynolds numbers firmly in the sub-critical range. However, it may be dangerous to use directly concepts derived for steady flow to describe phenomena observed in oscillatory flow. As KC becomes very large it may be permissible to consider the flow as quasi-steady but at most KC values observed in practice the flow is strongly influenced by unsteady effects. These will affect boundary layer stability, transition and separation. Hence a whole new set of loading coefficients has had to be derived for cylinders in oscillatory flow (see, for example, Sarpkaya and Isaccson (18)).
A number of authors, including Bearman et al. (19), Bearman (20), Williamson (21) and Obasaju et al. (22), have studied vortex shedding patterns developed by a circular cylinder in oscillatory flow. For KC values of order unity or less, depending on the value of β, the flow remains attached during a flow cycle and strictly the cylinder should not be described as bluff. As KC increases above this threshold value the flow separates during a flow cycle and at first a pair of weak vortices are formed during each half cycle. At the end of a half cycle these vortices are convected back on to the cylinder and may be destroyed by mixing with opposite sign vorticity or, as KC increases, they may survive to influence the vortex activity in the next half cycle. With increasing KC more circulation is generated and shed from the separation points during a half cycle and hence the vortices become stronger. Associated with this strengthening, the vortices become disturbed from their pattern of symmetry and unsteady transverse forces are developed. The root mean square transverse force coefficient reaches a maximum at a KC value of around 10 to 12 where presumably the vortices are at their strongest. With further increases in KC a vortex is shed before the end of the half cycle and a third vortex begins to form. During the wake re encounter process, under the influence of the other vortices, this new vortex passes around the cylinder and acts as the nucleus for the first vortex forming in the next half cycle from the diametrically opposite point from which it was formed. As KC is increased further this third vortex gains more circulation before the end of the half cycle. When it approaches the strength of a fully formed vortex it convects back over the cylinder on the same side on which it was initially formed. It now acts as a free vortex and accelerates the development and shedding of an opposite sign vortex from the other side of the cylinder and together they convect away under the influence of their mutual velocity fields. For KC values where the third vortex is about half fully formed at the end of a half cycle it may pass either under or over the cylinder causing apparently random changes to the transverse force time history. This general pattern of behaviour is repeated as KC is increased with the next partly formed vortex influencing the flow.
It is clear from the above description that there will be some KC values where the vortex flow pattern is stable and intermediate values where it exhibits an apparently chaotic behaviour. If for a moment we neglect the influence of flow history and assume that during a half cycle the flow behaves in a quasi-steady manner then we can estimate the number of vortices that will be formed. The number of vortices shed per second from one shear layer of a bluff body in a steady flow U is given by SU/D. If we assume that S remains constant in an oscillatory flow then the instantaneous shedding frequency is given by SÛsin (2πt/T)/D. Integrating this over half a flow cycle shows that a fully formed vortex will be generated each time KC increases by π/2S. Assuming S to be 0.2 then the predicted KC increment is just under 8. This agrees quite well with flow visualisation studies and suggests, for example,
that if two fully formed vortices are formed during a half cycle at KC=12, then three full vortices will be formed at KC=20. At KC=16 the vortex shedding pattern is likely to be unstable. This acute sensitivity to changing KC number makes the flow around a circular cylinder in oscillatory flow particularly difficult to predict.
No review of bluff bodies in oscillatory flow or waves would be complete without some discussion of the applicability of Morison's equation. This is an empirical equation, devised by Morison et al (23), to represent in-line loading on bodies in waves and was formulated in advance of much of the research that has been carried out into the flow around cylinders in oscillatory flow. The load per unit length, F(t), is given by:
where CD and CM are the drag and inertia coefficients respectively. It was envisaged by Morison et al that these coefficients would be derived from experiment but it is now possible, under certain limited conditions, also to calculate them using CFD. The two terms in the above equation are interpreted as the drag contribution and the inertia contribution because of their relation to the flow velocity and acceleration respectively. For a bluff body in a viscous oscillatory flow the generation and shedding of vortices develops forces which are not necessarily in phase with velocity and so, in addition to generating a drag force, vortices affect the value of the inertia coefficient. At low KC values where we know vortex shedding is weak or even non-existent the inertia coefficient for a circular cylinder is found to be close its inviscid value of 2. When vortex shedding is thought to be at its strongest, around KC=10, the added mass contribution to the inertia coefficent is small and at some β values may even be negative. Physically this is perfectly acceptable and simply reflects the fact that vortices do not necesarily induce an in-line force that is in phase with flow velocity.
In general the comparison between measured in-line force time histories and those predicted using Morison's equation is remarkably good. A number of attempts have been made to improve on Morison but none have been sufficiently successful to permit them to find their way into the design process. The agreement between Morison and measurements is, perhaps as is to be expected, worst at around KC=10 where there is very strong vortex activity. In addition to contributing to the in-line force, vortices also generate transverse forces and while there are equivalent model equations to predict transverse forces in planar oscillatory flow (see, for example, Verley (24) and Bearman et al. (25)), it is not clear how best these should be applied to a vertical cylinder in waves where KC is varying, with depth. From the earlier discussion on vortex shedding patterns it is clear that this KC variation will result in differences in the frequency of the transverse force with depth. Also if the KC is such that there is not a stable vortex pattern established then it is possible that the phase of the transverse force may vary by about 180° over quite short axial lengths of the cylinder. Hence in design transverse forces are often ignored on the argument that they are likely to be poorly correlated over a long length of cylinder. How best to predict the correlation length remains an open question.
NUMERICAL SIMULATION OF OSCILLATORY FLOW PAST A CIRCULAR CYLINDER
Several numerical solutions of the unsteady, two dimensional Navier Stokes equations for flow around a circular cylinder at low KC and relatively low β parameter have been reported in the literature. A version of the discrete vortex method has been used by Smith and Stansby (26) to calculate forces for KC values up to 4. A finite difference method, based on the stream function-vorticity formulation, was used by Justesen (27) and Zhang and Zhang (28) employed a finite volume method with primitive variables. Lin et al (29) have carried out simulations up to a KC of 36, for a relatively a low value of the β parameter, using the so called hybrid discrete vortex method due to Graham (30). Following the development of the discrete vortex method by Chorin (31), (32) it has been used in a wide variety of applications, as discussed by Sarpkaya (33). The method uses point vortices to represent regions of vorticity in the flow and a two step algorithm is employed to calculate separately convection and diffusion of these vortices. In the code used by Lin et al convection is accomplished by a Lagrangian scheme based on the cloud-in-cell method, while diffusion is carried out with a finite difference method, using the cloud-in-cell mesh. This hybrid Lagrangian/Eulerian approach has been applied by Cozens (34) to study roll damping of ships due to vortex formation and shedding, and by Arkell et al (35) to investigate the wake of a circular cylinder in
a combined wave and current flow. More recently, Meneghini and Bearman (36) used the same method to study the flow about a circular cylinder forced to oscillate transversely to a steady current.
Numerical simulation methods that can achieve an acceptable level of accuracy are presently limited to low values of β because of the difficulties of resolving thin boundary layers and other small scale motions. All the methods mentioned above are restricted to two-dimensional flow although there are already some three dimensional simulations emerging for very low KC values. The development of numerical simulation poses new challenges for experimentalists. In the design problem data is required at as high a value of β as possible whereas to validate numerical solutions very low β results are needed. In practice loading data in oscillatory flow is often obtained by mounting a cylinder in a U tube apparatus driven at its natural period. Low β can be achieved by making D small but then the loading also becomes small and difficult to measure accurately. By increasing the length of the water column in the U tube, which often is not a practical possibility, T can be increased but again the actual loading will be small. At Imperial College a new set of experimental measurements of drag and inertia coefficients for a range of KC and for a low β parameter of 70 has recently been obtained by Kuhtz (37). She replaced the water in the Imperial College U tube with a high viscosity water glycol mixture which enabled her to use a sufficiently large cylinder diameter to give accurate force measurements. Vortex shedding patterns at low values of β have been observed by Tatsuno and Bearman (38) using flow visualisation and these are also available for comparison with numerical simulations.
Table 6 Force coefficients calculated cycle by cycle
|
KC |
2.0 |
10.0 |
24. |
|||
|
Cycle |
CM |
CD |
CM |
CD |
CM |
CD |
|
2 |
2.2218 |
1.7335 |
1.8404 |
1.5549 |
1.4105 |
2.0128 |
|
3 |
2.2225 |
1.7436 |
2.0377 |
1.5036 |
1.6975 |
1.4868 |
|
4 |
2.2234 |
1.7438 |
2.0180 |
1.5212 |
0.8748 |
1.4908 |
|
5 |
2.2248 |
1.7375 |
1.7519 |
1.9222 |
1.6503 |
1.6236 |
|
6 |
2.2251 |
1.7229 |
1.6364 |
1.9383 |
0.8474 |
1.2015 |
|
7 |
2.2265 |
1.7356 |
1.4232 |
1.6836 |
3.2107 |
1.3909 |
|
8 |
2.2253 |
1.7305 |
2.1087 |
1.4305 |
1.6183 |
2.0592 |
|
9 |
2.2263 |
1.7226 |
1.8800 |
1.4875 |
0.8591 |
1.5127 |
|
10 |
2.2258 |
1.7212 |
1.7260 |
1.6388 |
0.7449 |
1.5481 |
|
11 |
2.2269 |
1.7207 |
1.9686 |
1.3787 |
0.5359 |
0.6681 |
|
12 |
2.2265 |
1.7234 |
1.6678 |
1.4558 |
1.5706 |
1.6501 |
|
13 |
2.2257 |
1.7164 |
1.6107 |
1.7831 |
0.5893 |
2.0629 |
|
14 |
2.2262 |
1.7175 |
1.1891 |
1.6347 |
1.3549 |
1.5429 |
|
15 |
2.2260 |
1.7203 |
2.0274 |
1.8365 |
1.3036 |
1.9965 |
|
16 |
2.2264 |
1.7189 |
0.9485 |
2.5663 |
1.7632 |
1.4651 |
|
17 |
2.2261 |
1.7181 |
1.3007 |
1.6059 |
1.1826 |
1.7758 |
|
18 |
2.2265 |
1.7167 |
1.9486 |
1.3374 |
2.0329 |
1.4744 |
|
19 |
2.2271 |
1.7121 |
1.7526 |
1.9175 |
1.7615 |
1.9998 |
|
20 |
2.2261 |
1.7139 |
1.2197 |
2.0437 |
1.2437 |
1.5261 |
|
21 |
2.2268 |
1.7136 |
1.0763 |
1.9665 |
1.6612 |
2.1811 |
|
22 |
2.2266 |
1.7139 |
0.9362 |
2.2909 |
0.5750 |
1.7843 |
|
23 |
2.2269 |
1.7157 |
1.2732 |
1.8460 |
0.6186 |
2.5953 |
|
24 |
0.9296 |
2.2094 |
2.6571 |
1.4261 |
||
Details of the computations to be desrcibed here for β=70 can be found in the paper by Lin et al (29); only a small selection of the results will be presented. CM and CD are obtained from Morison's equation on a flow cycle by flow cycle basis by applying a standard Fourier averaging process to computed time histories of the in-line force. Then mean values of the coefficients are found over a number of cycles. At small KC values the variation of the force coefficients from cycle to cycle is small but at larger KC, where there is shedding of strong vortices, the variations can become large. Hence the values of the Morison force coefficients will depend to some extent on the number of flow cycles computed. Typically 24 flow cycles were simulated and the force coefficients were averaged over the last 18 flow cycles. To illustrate the cycle by cycle variations results are presented in Table 1 for KC= 2, 10 and 24. It can be seen that the variations become much larger as KC increases. Similar variations are observed in experiment even though the U tube is operating at a constant frequency. Once again this illustrates the influence of wake re encounter which introduces a random factor into the flow.
CM and CD averaged over 18 cycles are shown plotted in Figures 10 and 11 respectively (note that Wu's method and the dp/dr method, which are fully explained in Lin et al, refer to two ways of calculating pressure forces). Also shown in figures 10 and 11 are drag and inertia coefficients measured by Kuhtz (37) for β=70. The numerical predictions do not reproduce the rapid rise of CD and decrease of CM at KC values around 8, although the predictions of CM are generally closer to the experimental data than those of CD. In particular, the peak in CD measured at around KC=10 is missing from the predictions. The reason for this is rather puzzling and may be related to three-dimensional flow features which cannot be reproduced by a two-dimensional simulation. However, it is interesting to note from figure 12, where measured and computed root mean square inline force coefficients are plotted, that the predicted r.m.s force coefficients agree well with the experimental results throughout the KC range examined. At larger KC (16–30), the computed CD values appear to agree quite well with those from the experiments. At KC above 30 the values of CM predicted by the two methods used to calculate forces deviate significantly from each other. At these KCs the inertia component represents a small proportion
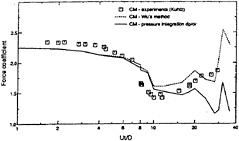
Figure 10 Computed and measured inertia coefficients for β=70
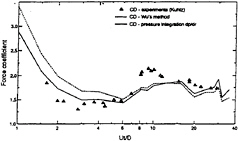
Figure 11 Computed and measured drag coefficients for β=70
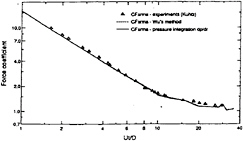
Figure 12 Computed and measured r.m.s. force coefficients for β=70
of the total force and in terms of overall loading these differences are insignificant. Nevertheless it is important to try to understand why these variations occur and it seems likely that there may be a slight phase difference in the total force computed by the two methods. A thorough study of time step, mesh resolution etc. would be needed to resolve this question.
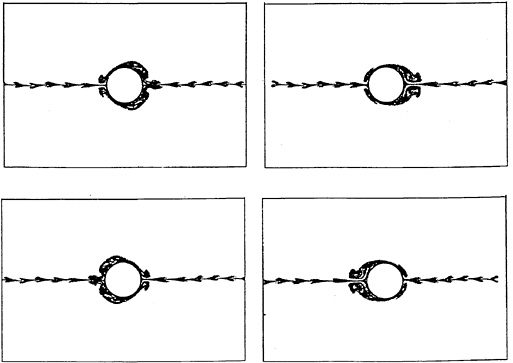
Figure 13 Numerical flow visualisation for KC=3 and β=70
During the course of the numerical study a considerable amount of data was generated relating to the velocity field about a circular cylinder in an oscillatory flow. In order to be able to view the data it was presented in the form of computed flow visualisations. These can then be compared with actual flow visualisations performed in water, such as those by Tatsuno and Bearman (38). With the discrete vortex method, recording the positions of the point vortices provides a relatively simple method of visualising the flow. However, in a flow visualisation experiment it is particles that are observed rather than point vortices and the resulting flow patterns may appear quite different. Tatsuno and Bearman (38) employed an electrolytic precipitation method in which fine white particles are released from the surface of the cylinder and initially they mark the vorticity generated at the surface. However, these particles are passive markers and will not retain their original vorticity. In order to provide a direct comparison between physical and computed visualisations, passive particles were introduced near the cylinder surface in the computations and their subsequent motion followed.
Two sample computed visualisations will be presented. Figure 13 shows the flow in the symmetric vortex regime at KC=3 and at various stages during a flow cycle. The particles concentrate into blobs and convect away to either side of the cylinder. These plots closely resemble the photograph presented in figure 4 of Tatsuno and Bearman (38). Figure 14 shows a visualisation for KC=10, with the flow oscillating from left to right. In this regime the majority of the vortex activity occurs either above or below the cylinder. In the example shown the main vortex activity is above the cylinder. It is at this KC value that the drag coefficient and the transverse force coefficient take their maximum values.
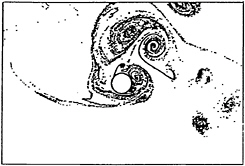
Figure 14 Numerical flow visualisation for KC=10 and β=70
THE RESPONSE OF FLEXIBLE CYLINDERS IN OSCILLATORY FLOW
A flexible circular cylinder mounted normal to a steady current flow is susceptible to flow induced vibration, depending on the level of damping and the non-dimensional mass ratio M/ρ D2, where M is the mass per unit length of the cylinder and ρ is the density of the fluid. Large transverse oscillations may occur when the frequency of vortex shedding coincides with the natural frequency of the cylinder. If the mass and damping are sufficiently small, in line oscillations may also be excited; although they will be of a much lower amplitude. In a relatively dense fluid such as water vortex excited oscillations can pose a serious problem. Much has been written about this phenomenon and readers are referred elsewhere for a detailed account.
In a planar oscillatory flow or in waves a flexible cylinder can also be excited into vibration, both in-line and transverse to the flow. Measurements of the response of a circular cylinder in oscillatory flow have been presented by Bearman et al. (39). At most values of KC the general form of the response in the in-line direction can be estimated quite successfully by using as input the unsteady force predicted by Morison's equation. In this application of the equation the force coefficients used are those appropriate to a fixed cylinder and the velocity and acceleration are relative to the responding cylinder. This is the so called “relative motion form” of Morison's equation. Figure 15 shows an example of the response and the associated prediction for a frequency ratio of around 2. The frequency ratio is defined as the ratio of the cylinder frequency measured in still water to the flow oscillation frequency. Measuring the cylinder frequency in still water is easy to do but it is not clear that this is the most appropriate frequency. Other frequencies that might be used are the frequency in air and the frequency in oscillating water.
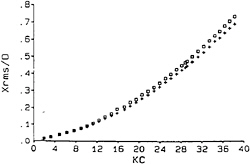
Figure 15 In-line response versus KC for a frequency ratio of 2; ☐, measured, +, predicted using Morison
When the frequency ratio is near 3 application of Morison's equation seriously under estimates the response over a KC band from about 8 to 25, as can be seen from figure 16. The frequency ratio as defined above for this case is 2.85 but the cylinder is observed to respond at precisely three times the flow frequency. There is clearly more excitation at three times the flow frequency than that which arises from the drag term in Morison 's equation. The extra response is thought to be due to the influence of vortex shedding. Using the numerical simulation procedure outlined above we have predicted the response for a flexible cylinder over a broad range of KC. However, to date we have been unable to reproduce the responses shown in figure 16 for KC values between about 8 and 25. We have carried out various checks on the experimental data and believe it to be correct and hence are unable to explain the discrepancy.
Bearman and Mackwood (40) have presented measurements of the transverse response of a flexible cylinder in oscillatory flow and some sample results are shown in figure 17 for a variety of frequency ratios. In these cases we know that the response is due directly to vortex shedding and it will be noted that the KC value for maximum response increases with increasing frequency ratio. It
has been pointed out earlier that the number of vortices shed per half cycle increases by one every time KC is increased by about 8. Hence we can expect vortex-excited response over a range of KC for each frequency ratio and for the KC at the centre of that range to increase with increasing frequency ratio. In the transverse direction the cylinder is forced to oscillate at an integer multiple of the flow frequency since the vortex shedding force is also at a multiple of the flow frequency.
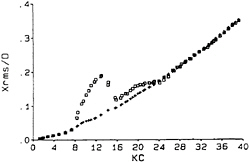
Figure 16 In-line response versus KC for a frequency ratio of 2.85; ☐, measured, +, predicted using Morison
Computations to predict the transverse response of a flexible cylinder have been reported by Bearman et al. (41), using the discrete vortex method described by Lin et al (29). The most marked difference between the experimental and computational flow environments is that one is three dimensional while the other is two dimensional. However, in experiments the motion of the cylinder is expected to force much of the flow into predominantly two-dimensional motion and hence it is believed that the flow code should give realistic predictions of cylinder response. Figure 18 shows a comparison between computed and measured root mean square response amplitudes for a range of KC values. The agreement is remarkably good and it would appear that the computational method has successfully captured the physics of the complex fluid structure interaction that takes place. The onset of oscillation and the sharp rise in amplitude for KC values in the range 3 to 4 are well predicted.
CONCLUSIONS
Bluff body hydrodyanmics is important in a number of naval applications and is particularly important in
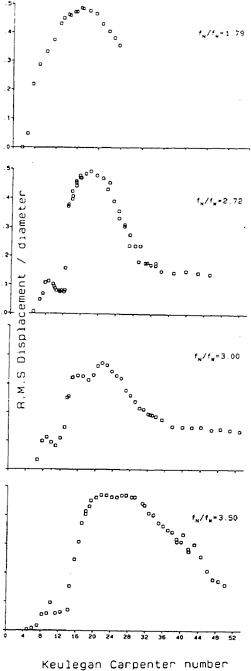
Figure 17 Transverse response versus KC for various ratios of the frequency of the model to the flow frequency
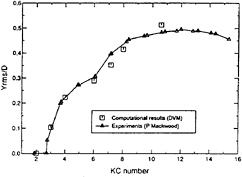
Figure 18 Transverse response versus KC; comparison of computed and experimental results for a frequency ratio of 1.81
certain aspects of the design of offshore structures. While much research has been directed towards the study of two-dimensional bluff bodies the instantaneous flows generated by such bodies can be far from two dimensional. The correlation length associated with vortex shedding from a rigid bluff body is a critical flow quantity but presently it cannot be predicted. In oscillatory flow and waves the return of vortices already shed play a significant role in the flow development. There are some values of Keulegan Carpenter number where shedding patterns are quite stable while at others, when perhaps a half formed vortex is left at the end of a cycle, there are substantial cycle to cycle variations. For a flexible circular cylinder in an oscillatory flow both in-line and transverse oscillations can be excited. In the in-line direction the response can be well predicted by applying the relative motion form of Morison's equation, except when the cylinder frequency is near to three times the flow frequency. In this case substantially larger responses are recorded which presumably are related to vortex shedding. Vortex shedding is directly responsible for vibrations in the transverse direction and as the cylinder frequency ratio increases so the Keulegan Carpenter number for maximum response increases. CFD is being increasingly used to study circular cylinders in oscillatory flow and in order to validate these codes more experimental data is required, particularly at low values of β.
ACKNOWLEDGEMENTS
The author would like to acknowledge the support of the US Office of Naval Research for work into three-dimensional aspects of bluff body flow and the EPSRC and the offshore industry, through MTD Ltd, for support of research into oscillatory flow past bluff bodies.
REFERENCES
1. Roshko A., “Perspectives on Bluff Body Aerodynamics,” J. Wind Eng. & Ind. Aero., Vol. 49, 1993, pp. 79–100.
2. Roshko A., “On the Wake and Drag of Bluff Bodies,” J. Aero. Sci., Vol. 124, 1995, pp 124–132.
3. Roshko A., “A New Hodograph for Free Streamline Theory,” NACA Tech Note 3168, 1954.
4. Griffin O.M., “Universal Similarity in the Wakes of Stationary and Vibrating Bluff Structures,” ASME J. of Fluids Eng., Vol. 103, No. 1, 1981, pp 52–58.
5. Szepessy S., “On the Spanwise Correlation of Vortex Shedding from a Circular Cylinder at High Reynolds Number,” Phys. Fluids, Vol. 6, No. 7, 1994, pp 2406–2416.
6. Gerrard J.H., “The Three-dimensional Structure of the Wake of a Circular Cylinder, ” J.Fluid Mech., Vol. 25, 1966, pp 143–164.
7. Williamson C.H.K., “Oblique and Parallel Modes of Vortex Shedding of a Circular Cylinder, ” J.Fluid Mech., Vol. 206, 1989, pp 579– 627.
8. Eisenlohr H. and Eckelmann H., “Vortex Splitting and its Consequences in the Vortex Street Wake of Cylinders at Low Reynolds Numbers,” Phys. Fluid., A1, 1989, pp 189–192.
9. Hammache M. and Gharib M., “An Experimental Study of the Parallel and Oblique Shedding from Circular Cylinders,” J.Fluid Mech., Vol. 232, 1991, pp 567–590.
10. Bearman P.W. and Tombazis N., “The Effects of Three-dimensional Imposed Disturbances on Bluff Body Near Wake Flows,” J.Wind Eng. & Ind. Aero., Vol. 49, 1993, pp 339–350.
11. Triantafyllou G.S., “Three-dimensional Flow Patterns in Two-dimensional Wakes,” ASME Symp. on Non-Steady Fluid Dynamics, FED Vol 92, 1990, pp 395–402.
12. Wei T. & Smith C.R., “Secondary Vortices in the Wake of a Circular Cylinder,” J.Fluid Mech., Vol. 169, 1986, pp 513–533.
13. Monkewitz P.A. & Nguyen L.N., “Absolute Instability in the Near-wake of Two-dimensional Bluff Bodies, ” J.Fluids & Struct., Vol. 1, 1987, pp 165–184.
14. Szepessy S. & Bearman P.W., “Aspect Ratio and End Plate Effects on Vortex Shedding from a Circular Cylinder,” J.Fluid Mech., Vol. 234, 1992, pp 191–218.
15. Graham J.M.R., “Comparing Computation of Flow Past Circular Cylinders with Experimental Data,” Bluff Body Wakes, Dynamics and Instabilities, Springer Verlag, Berlin, 1993, pp 317–324.
16. Bearman P.W., “Vortex Shedding from Oscillating Bluff Bodies,” Ann. Rev. Fluid Mech., Vol. 16, 1984, pp 195–222.
17. Bearman P.W., “Investigation of the Flow behind a Two-dimensional Model with a Blunt Trailing Edge and Fitted with Splitter Plates,” J.Fluid Mech., Vol. 21, 1965, pp 241–255.
18. Sarpkaya T. and Isaacson M., Mechanics of Wave Forces on Offshore Structures, Van Nostrand Reinhold, New York, 1981.
19. Bearman P.W., Graham J.M.R., Naylor P. and Obasaju E.D., “The Role of Vortices in Oscillatory Flow about Bluff Cylinders,” Proc. Intl. Symp. on Hydrodynamics in Ocean Eng., Trondheim, Norway, August, 1981, pp 621–635.
20. Bearman P.W., “Vortex Trajectories in Oscillatory Flow,” Proc. Intl. Symp. on Separated Flow around Marine Structures, Trondheim, Norway, June, 1985, pp 133–153.
21. Williamson C.H.K., “Sinusoidal Flow Relative to Circular Cylinders,” J.Fluid Mech., Vol. 155, 1985, pp 141–174.
22. Obasaju E.D., Bearman P.W. and Graham, J.M.R., “A Study of Forces, Circulation and Vortex Patterns around a Circular Cylinder in Oscillating Flow,” J. Fluid Mech., Vol. 196, 1988, pp 467–494.
23. Morison J.R., O'Brien M.P., Johnson J.W. and Schaaf S.A., “The Force Exerted by Surface Waves on Piles,” Petroleum Translations, Vol. 189, 1950, pp 149–157.
24. Verley R.L.P., “A Simple Model of Vortex-Induced Forces in Waves and Oscillating Currents,” Appl. Ocean Res., Vol. 4, 1982, pp 117–120.
25. Bearman P.W., Graham J.M.R. and Obasaju E.D., “A Model Equation for the Transverse Forces on Cylinders in Oscillatory Flows,” Appl. Ocean Res., Vol. 6, 1984, pp 166–172.
26. Smith P.A. and Stansby P.K., “Viscous Oscillatory Flows around Cylindrical Bodies at Low Keulegan-Carpenter Numbers Using the Vortex method,” J. Fluid and Structures, Vol. 51, 1991, pp 339–361.
27. Justesen P., “A Numerical Study of Oscillating Flow around a Circular Cylinder, ” J. Fluid Mech., Vol. 222, 1991, pp 157–196.
28. Zhang H.L. and Zhang X., “Flow Structure Analysis around an Oscillating Circular Cylinder at Low KC Number: a Numerical Study,” To be Published, 1996.
29. Lin X.W., Bearman P.W. and Graham J.M.R., “A Numerical Study of Oscillatory Flow about a Circular Cylinder for Low Values of Beta Parameter,” J.Fluid and Structures, Accepted for Publication, 1996.
30. Graham J.M.R., “Computation of Viscous Separated Flow Using a Particle Method,” Numerical Methods in Fluid Mechanics, Vol. 3, 1988, pp 310–317.
31. Chorin A.J., “Numerical Study of Slightly Viscous Flow,” J.Fluid Mech., Vol. 57, 1973, pp 785–796.
32. Chorin A.J. “Vortex Sheet Approximation of Boundary Layers,” J. Comput. Phys., Vol. 27, 1978, pp 428–442.
33. Sarpkaya T. “Computational Methods with Vortices—The 1988 Freeman Scholar Lecture,” J. of Fluids Engineering, Vol. 111, 1989, pp 5–52.
34. Cozens P.D., Numerical Modelling of the Roll Damping of Ships due to Vortex Shedding, PhD Thesis, University of London, 1987.
35. Arkell R.H., Graham J.M.R. and Zhou C.Y., “The Effects of Waves and Mean Flow on the Hydrodynamic Forces on Circular Cylinders,” Proc. of the 6th Int. BOSS Conf., London, UK. July, 1992, pp 445–455.
36. Meneghini J.R. and Bearman P.W., “Numerical Simulation of High Amplitude Oscillatory Flow about a Circular Cylinder,” J. of Fluids and Structures, Vol. 9, 1995, pp 435–455.
37. Kuhtz S., “Expermental Investigation of Oscillatory Flow around Circular Cylinders at Low β Numbers,” PhD Thesis in Preparation, University of London, 1996.
38. Tatsuno M. and Bearman P.W. “A Visual Study of the Flow around an Oscillating Circular cylinder at Low Keulegan Carpenter Numbers and Low Stokes numbers,” J. Fluid Mech., Vol. 211, 1990, pp 157–182.
39. Bearman P.W., Lin X.W. and Mackwood P.R., “Measurement and Prediction of Response of Circular Cylinders in Oscillating Flow,” Proc. of the 6th Int. BOSS Conf., London, UK. July, 1992, pp 297–307.
40. Bearman P.W. and Mackwood P.R., “Non-linear Vibration Characteristics of a Cylinder in an Oscillating Water Flow,” 5th Int. Conf. on Flow Induced Vibrations, I Mech E, 1991–6, 1991, pp 21–32.
41. Bearman P.W., Graham J.M.R., Lin X.W. and Mackwood P.R., “Modelling the Crossflow Resonse of Cylinders in Oscillatory Flow, ” Proc. of the 7th Int. BOSS Conf., MIT, Boston, USA, Pergamon, 1994, pp 827–844.



















