al., 1989). Data on colon cancer suggest five or six critical events (Vogelstein et al., 1988; Goyette et al., 1992). These examples suggest that more complex models might be required. Conceptually, the two-stage model could be extended to any number of stages.
The biologic basis of carcinogenesis is still incompletely understood. In spite of recent rapid advances at the molecular level, many of the events described cannot yet be demonstrated to be essential for the pathogenesis of cancer. Some might be incidental phenomena with no causal relationship to the carcinogenic process. Research utilizing dose-response modeling can provide insights into which events are necessary and sufficient to produce cancer by demonstrating which mechanistic assumptions are consistent with the dose-response data.
THE TWO-STAGE MODEL
The two-stage model developed by Moolgavkar, Venzon, and Knudson (Moolgavkar and Venzon, 1979; Moolgavkar and Knudson, 1981) postulates two critical events in carcinogenesis that are specific, irreversible, and hereditary (at the cell level). The model supposes three cell compartments: normal stem cells, intermediate cells that have been altered by one genetic event, and malignant cells that have been altered by two genetic events. The size of each compartment is affected by cell birth, death, and differentiation processes and by the rates of transition between cell compartments.
The model is consistent with current concepts regarding the roles of inactivated tumor-suppressor genes and activated oncogenes in carcinogenesis. It explicitly accounts for many processes considered important in carcinogenesis, including cell division, mutation, differentiation, and death and the clonal expansion of populations of cells. Although the various carcinogenic processes might have more than two steps, a major assumption is that each of them can be described as consisting of two critical, genomic events: the first is assumed to give a small growth advantage through partial abrogation of growth control, and the second is assumed to lead to total abrogation of growth control. Among the other assumptions are that a cancer arises from a single cell, that transformations of stem cells are independent events, that each transformed cell will become a tumor, and that the time required to develop from a single transformed cell into a tumor is constant.
The mathematical aspects of two-stage model development and application have been described by Moolgavkar, Cohen, and Portier and their associates (Greenfield et al., 1984; Portier, 1987; Ellwein and Cohen, 1988; Moolgavkar, 1988; Moolgavkar and Luebeck, 1990; Portier and Edler, 1990; Tan, 1991). The model permits computation of both the rate at which tumors form (incidence function) and the probability of tumor formation with respect to time. Both stochastic and deterministic forms of the model have been described.
In the schematic representation of the model (Figure 1) as described by Moolgavkar and Knudson (1981), C0, C1, C2, and D represent stem cells, intermediate cells, malignant cells, and differentiated or dead cells. A normal stem cell can divide into two stem cells, die, or be transformed by mutation into an altered intermediate cell. An intermediate cell similarly divides into two intermediate cells, dies, or becomes transformed into a fully malignant cell. a1 is the rate at which cells divide (normal cells at a1, and intermediate cells cells at a2), ß1 the rate at which they die, and µ1 the rate at which they are transformed.
That formulation assumes that normal cells behave independently, which implies that they either die out (generally early in life, which would result in death of the subject) or grow exponentially throughout life. Neither alternative is realistic, so the normal stem cell population
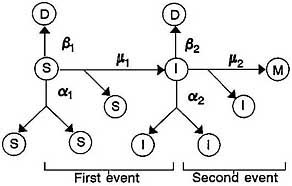
FIGURE 1 Two-stage model paradigm. Source: Moolgavkar and Knudson, 1981.
is generally modeled as growing deterministically, with intermediate cells arising from normal cells in a nonhomogeneous Poisson process with intensity function X(s)v(s), where X(s) is the (deterministic) size of the normal stem cell population at age s and v(s) is the rate at which stem cells are converted into intermediate cells. With that form of the model, closed-form mathematical expressions can be obtained for the probability of forming a malignant cell by time t, P(t), and the associated instantaneous-hazard function h(t), as long as the parameters are time-independent. By integrating Expression 24 of Moolgavkar et al. (1988), one obtains
and
where
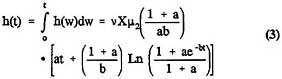
and
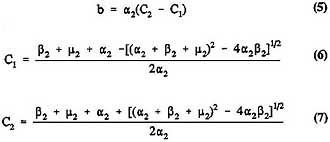
X(s) and (s) are not separately identifiable, and only their product can be estimated. Intermediate cells behave independently and with exponentially distributed lifespans. Consequently, clones of intermediate cells either die out or increase exponentially in size; there is no provision for growth regulation. Those assumptions are unrealistic, and alternatives have been proposed (Moolgavkar and Luebeck, 1990); however, implementation of more realistic alternatives greatly complicates the mathematical analysis and may not be necessary in providing good estimates of h(t).
The time between the occurrence of the first malignant cell and a clinically detectable cancer or death is generally modeled as a constant (Moolgavkar and Luebeck, 1990). A different assumption could easily be made, but doing so is likely to make the resulting mathematics intractable.
Before the model can be used in risk assessment, the effect of does must be incorporated. That is generally accomplished by treating model parameters as functions of instantaneous dose (Thorslund et al., 1987; Moolgavkar and Luebeck, 1990). Dose can be incorporated into the model by introducing a dose-effect relationship into the transition rate from normal cells to intermediate cells (µ1), into the transition rate from intermediate cells to malignant cells (µ2 ), or into the growth rate of clones of intermediate cells (a2 -ß2). If the dose rate changes over time, then the corresponding parameter that dose affects is time-dependent and the solutions presented earlier do not apply. Explicit formulas for obtaining solutions when the parameters are piece-wise constant are also found in Moolgavkar and Luebeck (1990). Quinn (1989) and Moolgavkar and Luebeck (1990) showed how to obtain numerical solutions with
the method of characteristics when the parameters are generally time-dependent.
One of the most important applications of dose-response models in risk assessment is to predict increased risk from exposure to low doses of a chemical. Typically, increased cancer risks on the order of 1/100 cannot be accurately measured in either a standard animal bioassay or an epidemiologic study due to limitations of sample size, yet increased risks in human populations of this magnitude, and even smaller, are of concern.
Small increased risks from low exposures are often estimated by fitting a dose-response model to data collected at higher exposures. The form assumed for the dose-response model is of critical importance to the resulting risk estimate (NRC, 1983). Regulatory agencies have frequently applied models that assume the increased risk is linearly related to exposure (i.e., the increased risk is proportional to the amount of exposure), at least at low exposures. However, it is frequently the case that nonlinear models will fit the data equally well and predict much lower risks at low exposures. The most extreme case of a nonlinear model is a threshold model, which assumes that there is a critical exposure (i.e., a threshold) below which the risk is not increased.
As is the case with simpler descriptive models, the manner in which the effect of dose is modeled will be the determining factor in the predictions of the two-stage model at low doses. If at least one of the transition rates is assumed to vary linearly with dose at low doses and the background incidence of cancer is not zero, then the probability of cancer will vary linearly with dose at low doses, although the low dose linear slope could differ appreciably from that predicted from high dose data. However, if all the dose-related rates are assumed to vary nonlinearly with dose at low doses or to exhibit a threshold dose below which the rate is not affected by dose, then the probability of cancer will likewise vary nonlinearly with dose at low doses or exhibit a threshold below which dose cannot cause cancer, respectively. Consequently, the manner in which dose is introduced into the two-stage model is a critical assumption for risk assessment.
Depending on how the model parameters are selected, there might be a number of parameters to estimate. For example, in their application of the two-stage model to data on 1,797 rats exposed to radon, Moolgavkar and Luebeck (1990) assumed that the number of normal cells was a constant and a clone of malignant cells of any size could be identified as
a tumor at necropsy. They also assumed that the rate at which intermediate cells divided (2) was 10 times per week—the measured cell division rate for adenomas in rat lungs. Despite those simplifying assumptions, six parameters still had to be estimated by fitting the model to the cancer bioassay data. Although those data constituted an extraordinarily large data set, the precision with which some of the parameters could be estimated from the tumor data was low.
Application of a six-parameter model illustrates one of the key advantages of the two-stage model, as well as one of its disadvantages. Unlike the parameters of descriptive models (e.g., statistical models not derived from underlying biologic mechanisms), the parameters of the two-stage model are required to relate to actual biologic phenomena. Thus, Moolgavkar and Luebeck made the assumption that intermediate cells are equivalent to adenoma cells. This assumption implies that adenomas progress to carcinomas and is open to investigation. Generally, the two-stage model is more useful than mainly descriptive models for testing mechanistic hypotheses of this type, because several models can be developed based on alternative biologic hypotheses, which can then be tested on the basis of goodness-of-fit. Descriptive models are developed by fitting them to data, and hypotheses regarding underlying biologic mechanisms generally cannot be tested on the basis of fit.
A disadvantage of the two-stage model illustrated by the analysis of Moolgavkar and Luebeck is the potentially large number of model parameters to be estimated. To estimate as many as six parameters reliably might require large numbers of animals exposed to various dose patterns and with serial sacrifices. Thus, most examples of application of the two-stage model have used large data sets—e.g., the ED01 study of 2-AAF (Cohen and Ellwein, 1990) and the study involving 1,797 animals exposed to radon (Moolgavkar and Luebeck, 1990). Such extensive data sets are available for only a few chemicals.
An alternative to estimating large numbers of parameters from tumor bioassay data is estimating specific parameters with data from other sources. Moolgavkar and Luebeck's estimation of the cell division rate of intermediate cells on the basis of the cell division rate in adenomas illustrates the approach. Although the approach is potentially quite useful, the knowledge needed for its general application is not yet available. In general, it requires an understanding of the steps in carcinogenesis and identification of cell types produced in the progression from normal to






